5年高考真题精选与最新模拟备战数学（文） 专题08 立体几何 110页

【2012 高考真题精选】 1．（2012·重庆）设四面体的六条棱的长分别为 1,1,1,1， 2和 a，且长为 a 的棱与长为 2的棱异面，则 a 的取值范围为( ) A．(0， 2) B．(0， 3) C．(1， 2) D．(1， 3) 2．（2012·陕西）将正方体(如图 1－3①所示)截去两个三棱锥，得到图②所示的几何体，则该几何体的左视 图为( ) 3．（2012·安徽）若四面体 ABCD 的三组对棱分别相等，即 AB＝CD，AC＝BD，AD＝BC，则________(写出 所有正确结论的编号)． ①四面体 ABCD 每组对棱相互垂直；②四面体 ABCD 每个面的面积相等；③从四面体 ABCD 每个顶点 出发的三条棱两两夹角之和大于 90°而小于 180°；④连接四面体 ABCD 每组对棱中点的线段相互垂直平分； ⑤从四面体 ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长． 4．（2012·上海）一个高为 2 的圆柱，底面周长为 2π，该圆柱的表面积为________． π. 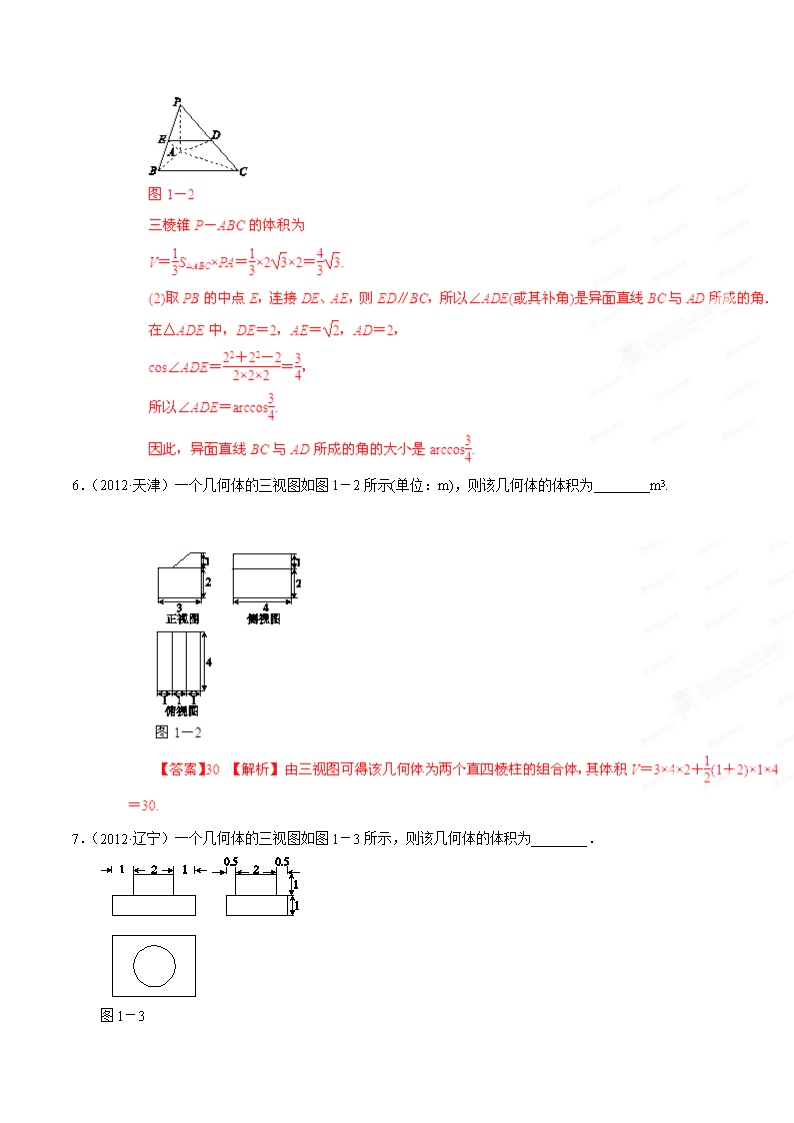5．（2012·上海）如图 1－1，在三棱锥 P－ABC 中，PA⊥底面 ABC，D 是 PC 的中点，已知∠BAC＝π 2 ， AB＝2，AC＝2 3，PA＝2，求： 图 1－1 (1)三棱锥 P－ABC 的体积； (2)异面直线 BC 与 AD 所成的角的大小(结果用反三角函数值表示)． 【答案】解：(1)S△ABC＝1 2×2×2 3＝2 3， 6．（2012·天津）一个几何体的三视图如图 1－2 所示(单位：m)，则该几何体的体积为________m3. 7．（2012·辽宁）一个几何体的三视图如图 1－3 所示，则该几何体的体积为________． 图 1－3 8．（2012·课标全国）如图 1－2，网格纸上小正方形的边长为 1，粗线画出的是某几何体的三视图，则此几 何体的体积为( ) 图 1－3 A．6 B．9 C．12 D．18 9. （2012·浙江）已知某三棱锥的三视图(单位：cm)如图 1－1 所示，则该三棱锥的体积是( ) A．1 cm3 B．2 cm3 C．3 cm3 D．6 cm3 10．（2012·陕西）将正方体(如图 1－3①所示)截去两个三棱锥，得到图②所示的几何体，则该几何体的 左视图为( ) 图 1－3 图 1－4 【答案】B 【解析】 分析题目中截几何体所得的新的几何体的形状，结合三视图实线和虚线的不同 表示可知对应的左视图应该为 B. 12.（2012·湖北）已知某几何体的三视图如图 1－4 所示，则该几何体的体积为________． 13．（2012·广东）某几何体的三视图如图 1－1 所示，它的体积为( ) 图 1－1 A．72π B．48π C．30π D．24π 【答案】C 【解析】 根据三观图知该几何体是由半球与圆锥构成，球的半径 R＝3，圆锥半径 R＝3， 高为 4，所以 V 组合体＝V 半球＋V 圆锥＝1 2×4 3π×33＋1 3π×32×4＝30π，所以选择 C. 14．（2012·福建）一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是( ) A．球 B．三棱锥 C．正方体 D．圆柱 【答案】D 【解析】 球的三视图大小、形状相同，三棱锥的三视图也可能相同，正方体三种视图也 相同，只有 D 不同． 15．（2012·安徽）某几何体的三视图如图 1－2 所示，则该几何体的体积等于________． 图 1－2 【答案】56 【解析】 如图，根据三视图还原的实物图为底面是直角梯形的直四棱柱，其体积为 V＝ Sh＝1 2 (2＋5)×4×4＝56. 16．（2012·北京）某三棱锥的三视图如图 1－4 所示，该三棱锥的表面积是( ) 图 1－4 A．28＋6 5 B．30＋6 5 C．56＋12 5 D．60＋12 5 17．（2012·湖南）某几何体的正视图和侧视图均如图 1－1 所示，则该几何体的俯视图不可能．．．是( ) 图 1－1 【答案】C 【解析】 本题考查三视图，意在考查考生三视图的辨析，以及对三视图的理解和掌握．选 项 A, B, D，都有可能，选项 C 的正视图应该有看不见的虚线，故 C 是不可能的． 18．（2012·江西）若一个几何体的三视图如图 1－2 所示，则此几何体的体积为( ) A.11 2 B．5[来源:Z#xx#k.Com] C.9 2 D．4 19．（2012·山东）如图 1－6，几何体 E－ABCD 是四棱锥，△ABD 为正三角形，CB＝CD，EC⊥BD. 图 1－6 (1)求证：BE＝DE； (2)若∠BCD＝120°，M 为线段 AE 的中点，求证：DM∥平面 BEC. 【答案】证明：(1)取 BD 的中点 O，连接 CO，EO. 由于 CB＝CD，所以 CO⊥BD， 又 EC⊥BD，EC∩CO＝C， CO，EC ⊂ 平面 EOC， 因为△ABD 为正三角形． 所以∠BAD＝60°，∠ABC＝90°， 因此∠AFB＝30°， 所以 AB＝1 2AF. 又 AB＝AD， 所以 D 为线段 AF 的中点． 连接 DM，由点 M 是线段 AE 的中点， 因此 DM∥EF. 又 DM⊄平面 BEC，EF ⊂ 平面 BEC， 所以 DM∥平面 BEC. 20．（2012·辽宁）如图 1－5，直三棱柱 ABC－A′B′C′，∠BAC＝90°，AB＝AC＝ 2，AA′＝1，点 M，N 分别为 A′B 和 B′C′的中点． (1)证明：MN∥平面 A′ACC′； (2)求三棱锥 A′－MNC 的体积． (锥体体积公式 V＝1 3Sh，其中 S 为底面面积，h 为高) 取 A′B′中点 P，连结 MP，NP， M、N 分别为 AB′与 B′C′的中点， 所以 MP∥AA′，PN∥A′C′， 所以 MP∥平面 A′ACC′，PN∥平面 A′ACC′， 又 MP∩NP＝P， 因此平面 MPN∥平面 A′ACC′，而 MN ⊂ 平面 MPN. 因此 MN∥平面 A′ACC′. (2)(解法一) 连结 BN，由题意 A′N⊥B′C′， 平面 A′B′C′∩平面 B′BCC′＝B′C′， 所以 A′N⊥平面 NBC. 又 A′N＝1 2B′C′＝1，故 VA′－MNC＝VN－A′MC＝1 2VN－A′BC＝1 2VA′－NBC＝1 6. (解法二) VA′－MNC＝VA′－NBC－VM－NBC＝1 2VA′－NBC＝1 6. 21．（2012·北京）如图 1－9(1)，在 Rt△ABC 中，∠C＝90°，D，E 分别为 AC，AB 的中点，点 F 为线 段 CD 上的一点，将△ADE 沿 DE 折起到△A1DE 的位置，使 A1F⊥CD，如图 1－9(2)． (1)求证：DE∥平面 A1CB； (2)求证：A1F⊥BE； (3)线段 A1B 上是否存在点 Q，使 A1C⊥平面 DEQ？说明理由． 21．（2012·江苏）如图 1－4，在直三棱柱 ABC－A1B1C1 中，A1B1＝A1C1，D，E 分别是棱 BC，CC1 上的点(点 D 不同于点 C)，且 AD⊥DE，F 为 B1C1 的中点． 求证：(1)平面 ADE⊥平面 BCC1B1； (2)直线 A1F∥平面 ADE. 因为 CC1⊥平面 A1B1C1，且 A1F ⊂ 平面 A1B1C1， 所以 CC1⊥A1F. 又因为 CC1，B1C1 ⊂ 平面 BCC1B1，CC1∩B1C1＝C1， 所以 A1F⊥平面 BCC1B1. 由(1)知 AD⊥平面 BCC1B1，所以 A1F∥AD. 又 AD ⊂ 平面 ADE，A1F⊄平面 ADE，所以 A1F∥平面 ADE. 22．（2012·浙江）设 l 是直线，α，β是两个不同的平面( )[来源:学&科&网] A．若 l∥α，l∥β，则α∥β B．若 l∥α，l⊥β，则α⊥β C．若α⊥β，l⊥α，则 l⊥β D．若α⊥β，l∥α，则 l⊥β 23．（2012·江西）如图 1－7，在梯形 ABCD 中，AB∥CD，E，F 是线段 AB 上的两点，且 DE⊥AB，CF⊥AB， AB＝12，AD＝5，BC＝4 2，DE＝4，现将△ADE，△CFB 分别沿 DE，CF 折起，使 A，B 两点重合于点 G， 得到多面体 CDEFG. (1)求证：平面 DEG⊥平面 CFG； (2)求多面体 CDEFG 的体积． 因为平面 CDEF⊥平面 EFG，得 GH⊥平面 CDEF， VCDEFG＝1 3SCDEF·GH＝16. 24．（2012·四川）如图 1－4，在正方体 ABCD－A1B1C1D1 中，M、N 分别是棱 CD、CC1 的中点，则异 面直线 A1M 与 DN 所成的角的大小是________. 图 1－4 【答案】90° 【解析】 因为 ABCD－A1B1C1D1 为正方体，故 A1 在平面 CDD1C1 上的射影为 D1， 即 A1M 在平面 CDD1C1 上的射影为 D1M， 而在正方形 CDD1C1 中，由 tan∠DD1M＝tan∠CDN＝1 2 ， 可知 D1M⊥DN， 由三垂线定理可知，A1M⊥DN. 25．（2012·重庆）已知在直三棱柱 ABC－A1B1C1 中，AB＝4，AC＝BC＝3，D 为 AB 的中点． (1)求异面直线 CC1 和 AB 的距离； (2)若 AB1⊥A1C，求二面角 A1－CD－B1 的平面角的余弦值． 图 1－3 5y1＝0， －2x1＋2 2z1＝0， 取 z1＝1，得 m＝( 2，0,1)． 设平面 B1CD 的法向量为 n＝(x2，y2，z2)，则 n⊥DC→ ，n⊥DB1 → ，即 5y2＝0， 2x2＋2 2z2＝0， 取 z2＝－1，得 n＝( 2，0，－1)，所以 cos〈m，n〉＝ m·n |m|·|n| ＝ 2－1 2＋1· 2＋1 ＝1 3. 所以二面角 A1－CD－B1 的平面角的余弦值为1 3. 26．（2012·浙江）设 l 是直线，α，β是两个不同的平面( ) A．若 l∥α，l∥β，则α∥β B．若 l∥α，l⊥β，则α⊥β C．若α⊥β，l⊥α，则 l⊥β D．若α⊥β，l∥α，则 l⊥β 27．（2012·浙江）如图 1－5，在侧棱垂直底面的四棱柱 ABCD－A1B1C1D1 中，AD∥BC，AD⊥AB，AB＝ 2， AD＝2，BC＝4，AA1＝2，E 是 DD1 的中点，F 是平面 B1C1E 与直线 AA1 的交点． (1)证明：(i)EF∥A1D1； (ii)BA1⊥平面 B1C1EF； (2)求 BC1 与平面 B1C1EF 所成的角的正弦值． 图 1－5 【答案】解：(1)证明：(ⅰ)因为 C1B1∥A1D1，C1B1⊄平面 A1D1DA，所以 C1B1∥平面 A1D1DA， 又因为平面 B1C1EF∩平面 A1D1DA＝EF， 28．（2012·天津）如图 1－4，在四棱锥 P－ABCD 中，底面 ABCD 是矩形，AD⊥PD，BC＝1，PC＝2 3， PD＝CD＝2. (1)求异面直线 PA 与 BC 所成角的正切值； (2)证明平面 PDC⊥平面 ABCD； (3)求直线 PB 与平面 ABCD 所成角的正弦值． 29．（2012·陕西）直三棱柱 ABC－A1B1C1 中，AB＝AA1，∠CAB＝π 2. (1)证明：CB1⊥BA1； (2)已知 AB＝2，BC＝ 5，求三棱锥 C1－ABA1 的体积． 图 1－7 【答案】解：(1)证明：如图，连结 AB1， ∵ABC－A1B1C1 是直三棱柱，∠CAB＝π 2 ， ∴AC⊥平面 ABB1A1，故 AC⊥BA1. 又∵AB＝AA1，∴四边形 ABB1A1 是正方形， ∴BA1⊥AB1，又 CA∩AB1＝A. ∴BA1⊥平面 CAB1，故 CB1⊥BA1. (2)∵AB＝AA1＝2，BC＝ 5，∴AC＝A1C1＝1， 由(1)知，A1C1⊥平面 ABA1， ∴VC1－ABA1＝1 3S△ABA1·A1C1＝1 3×2×1＝2 3. 30．（2012·课标全国）如图 1－4，三棱柱 ABC－A1B1C1 中，侧棱垂直底面，∠ACB＝90°，AC＝BC＝1 2AA1， D 是棱 AA1 的中点． (1)证明：平面 BDC1⊥平面 BDC； (2)平面 BDC1 分此棱柱为两部分，求这两部分体积的比． 故平面 BDC1 分此棱柱所得两部分体积的比为 1∶1. 31.（2012·山东）如图 1－6，几何体 E－ABCD 是四棱锥，△ABD 为正三角形，CB＝CD，EC⊥BD. 图 1－6 (1)求证：BE＝DE； (2)若∠BCD＝120°，M 为线段 AE 的中点，求证：DM∥平面 BEC. 32．（2012·湖南）如图 1－7，在四棱锥 P－ABCD 中，PA⊥平面 ABCD，底面 ABCD 是等腰梯形，AD∥BC， AC⊥BD. (1)证明：BD⊥PC； (2)若 AD＝4，BC＝2，直线 PD 与平面 PAC 所成的角为 30°，求四棱锥 P－ABCD 的体积． 【答案】解：(1)证明：因为 PA⊥平面 ABCD，BD ⊂ 平面 ABCD，所以 PA⊥BD. 图 1－8 又 AC⊥BD，PA，AC 是平面 PAC 内的两条相交直线，所以 BD⊥平面 PAC. 而 PC ⊂ 平面 PAC，所以 BD⊥PC. (2)设 AC 和 BD 相交于点 O，连结 PO，由(1)知，BD⊥平面 PAC，所以∠DPO 是直线 PD 和平面 PAC 所成的角．从而∠DPO＝30°. 由 BD⊥平面 PAC，PO ⊂ 平面 PAC 知，BD⊥PO. 在 Rt△POD 中，由∠DPO＝30°得 PD＝2OD. 因为四边形 ABCD 为等腰梯形，AC⊥BD，所以△AOD，△BOC 均为等腰直角三角形．从而梯形 ABCD 的高为 1 2AD＋1 2BC＝1 2×(4＋2)＝3，于是梯形 ABCD 的面积 S＝1 2×(4＋2)×3＝9. 在等腰直角三角形 AOD 中，OD＝ 2 2 AD＝2 2，所以 PD＝2OD＝4 2，PA＝ PD2－AD2＝4. 故四棱锥 P－ABCD 的体积为 V＝1 3×S×PA＝1 3×9×4＝12. 33．（2012·湖北）某个实心零部件的形状是如图 1－7 所示的几何体，其下部是底面均是正方形，侧面 是全等的等腰梯形的四棱台 A1B1C1D1－ABCD，上部是一个底面与四棱台的上底面重合，侧面是全等的矩形 的四棱柱 ABCD－A2B2C2D2. 图 1－7 (1)证明：直线 B1D1⊥平面 ACC2A2； (2)现需要对该零部件表面进行防腐处理．已知 AB＝10，A1B1＝20，AA2＝30，AA1＝13(单位：cm)，每 平方厘米的加工处理费为 0.20 元，需加工处理费多少元？ 34．（2012·广东）如图 1－5 所示，在四棱锥 P－ABCD 中，AB⊥平面 PAD，AB∥CD，PD＝AD，E 是 PB 的中点，F 是 DC 上的点且 DF＝1 2AB，PH 为△PAD 中 AD 边上的高． (1)证明：PH⊥平面 ABCD； (2)若 PH＝1，AD＝ 2，FC＝1，求三棱锥 E－BCF 的体积； (3)证明：EF⊥平面 PAB. 图 1－5 【答案】解：(1)由于 AB⊥平面 PAD，PH ⊂ 平面 PAD， 故 AB⊥PH. 35．（2012·安徽）如图 1－3，长方体 ABCD－A1B1C1D1 中，底面 A1B1C1D1 是正方形，O 是 BD 的中点，E 是棱 AA1 上任意一点． (1)证明：BD⊥EC1； (2)如果 AB＝2，AE＝ 2，OE⊥EC1，求 AA1 的长． 所以 AA1 的长为 3 2. 36．（2012·北京）如图 1－9(1)，在 Rt△ABC 中，∠C＝90°，D，E 分别为 AC，AB 的中点，点 F 为线 段 CD 上的一点，将△ADE 沿 DE 折起到△A1DE 的位置，使 A1F⊥CD，如图 1－9(2)． (1)求证：DE∥平面 A1CB； (2)求证：A1F⊥BE； (3)线段 A1B 上是否存在点 Q，使 A1C⊥平面 DEQ？说明理由． 37．（2012·江苏）如图 1－4，在直三棱柱 ABC－A1B1C1 中，A1B1＝A1C1，D，E 分别是棱 BC，CC1 上的点(点 D 不同于点 C)，且 AD⊥DE，F 为 B1C1 的中点． 求证：(1)平面 ADE⊥平面 BCC1B1； (2)直线 A1F∥平面 ADE. 因为 CC1⊥平面 A1B1C1，且 A1F ⊂ 平面 A1B1C1， 所以 CC1⊥A1F. 又因为 CC1，B1C1 ⊂ 平面 BCC1B1，CC1∩B1C1＝C1， 所以 A1F⊥平面 BCC1B1. 由(1)知 AD⊥平面 BCC1B1，所以 A1F∥AD. 又 AD ⊂ 平面 ADE，A1F⊄平面 ADE，所以 A1F∥平面 ADE. 38．（2012·全国）如图 1－1，四棱锥 P－ABCD 中，底面 ABCD 为菱形，PA⊥底面 ABCD，AC＝2 2， PA＝2，E 是 PC 上的一点，PE＝2EC. (1)证明：PC⊥平面 BED； (2)设二面角 A－PB－C 为 90°，求 PD 与平面 PBC 所成角的大小． 因为二面角 A－PB－C 为 90°，所以平面 PAB⊥平面 PBC. 又平面 PAB∩平面 PBC＝PB， 故 AG⊥平面 PBC，AG⊥BC. BC 与平面 PAB 内两条相交直线 PA，AG 都垂直，故 BC⊥平面 PAB，于是 BC⊥AB，所以底面 ABCD 因为面 PAB⊥面 PBC，故 m·n＝0，即 b－2 b ＝0，故 b＝ 2，于是 n＝(1，－1， 2)，DP→ ＝(－ 2，－ 2，2)， cos〈n，DP→ 〉＝ n·DP→ |n||DP→ | ＝1 2 ， 〈n，DP→ 〉＝60°. 因为 PD 与平面 PBC 所成的角和〈n，DP→ 〉互余， 故 PD 与平面 PBC 所成的角为 30°. 39．（2012·重庆）已知在直三棱柱 ABC－A1B1C1 中，AB＝4，AC＝BC＝3，D 为 AB 的中点． (1)求异面直线 CC1 和 AB 的距离； (2)若 AB1⊥A1C，求二面角 A1－CD－B1 的平面角的余弦值． ＝(2，5，－h)． 由AB1 → ⊥A1C→ 得AB1 → ·A1C→ ＝0，即 8－h2＝0，因此 h＝2 2. 40．（2012·山东）如图 1－3 所示，正方体 ABCD－A1B1C1D1 的棱长为 1，E 为线段 B1C 上的一点，则三棱 锥 A－DED1 的体积为________． 图 1－3 【答案】.1 6 【解析】 本题考查棱锥的体积公式，考查空间想象力与转化能力，容易题． VA－DED1＝VE－DD1A＝1 3×1 2×1×1×1＝1 6. 41．（2012·江苏）如图 1－2，在长方体 ABCD－A1B1C1D1 中，AB＝AD＝3 cm，AA1＝2 cm，则四棱锥 A －BB1D1D 的体积为________cm3. 42.（2012·浙江）已知某三棱锥的三视图(单位：cm)如图 1－1 所示，则该三棱锥的体积是( ) A．1 cm3 B．2 cm3 C．3 cm3 D．6 cm3 43．（2012·陕西）直三棱柱 ABC－A1B1C1 中，AB＝AA1，∠CAB＝π 2. (1)证明：CB1⊥BA1； (2)已知 AB＝2，BC＝ 5，求三棱锥 C1－ABA1 的体积． 44．（2012·湖南）如图 1－7，在四棱锥 P－ABCD 中，PA⊥平面 ABCD，底面 ABCD 是等腰梯形，AD∥BC， AC⊥BD. (1)证明：BD⊥PC； (2)若 AD＝4，BC＝2，直线 PD 与平面 PAC 所成的角为 30°，求四棱锥 P－ABCD 的体积． 【答案】解：(1)证明：因为 PA⊥平面 ABCD，BD ⊂ 平面 ABCD，所以 PA⊥BD. 图 1－8 又 AC⊥BD，PA，AC 是平面 PAC 内的两条相交直线，所以 BD⊥平面 PAC. 而 PC ⊂ 平面 PAC，所以 BD⊥PC. (2)设 AC 和 BD 相交于点 O，连结 PO，由(1)知，BD⊥平面 PAC，所以∠DPO 是直线 PD 和平面 PAC 所成的角．从而∠DPO＝30°. 由 BD⊥平面 PAC，PO ⊂ 平面 PAC 知，BD⊥PO. 在 Rt △ POD 中，由∠DPO＝30°得 PD＝2OD. 因为四边形 ABCD 为等腰梯形，AC⊥BD，所以 △ AOD， △ BOC 均为等腰直角三角形．从而梯形 ABCD 的高为 1 2AD＋1 2BC＝1 2×(4＋2)＝3，于是梯形 ABCD 的面积 S＝1 2×(4＋2)×3＝9. 在等腰直角三角形 AOD 中，OD＝ 2 2 AD＝2 2，所以 PD＝2OD＝4 2，PA＝ PD2－AD2＝4. 故四棱锥 P－ABCD 的体积为 V＝1 3×S×PA＝1 3×9×4＝12. 45．（2012·湖北）某个实心零部件的形状是如图 1－7 所示的几何体，其下部是底面均是正方形，侧面 是全等的等腰梯形的四棱台 A1B1C1D1－ABCD，上部是一个底面与四棱台的上底面重合，侧面是全等的矩形 的四棱柱 ABCD－A2B2C2D2. 图 1－7 (1)证明：直线 B1D1⊥平面 ACC2A2； (2)现需要对该零部件表面进行防腐处理．已知 AB＝10，A1B1＝20，AA2＝30，AA1＝13(单位：cm)，每 平方厘米的加工处理费为 0.20 元，需加工处理费多少元？ (A2B2)2＋4AB·AA2＝102＋4×10×30＝1 300(cm2)． 又因为四棱台 A1B1C1D1－ABCD 的上、下底面均是正方形，侧面是全等的等腰梯形． 所以 S2＝S 四棱台下底面＋S 四棱台侧面 ＝(A1B1)2＋4×1 2(AB＋A1B1)h 等腰梯形的高 ＝202＋4×1 2(10＋20) 132－ 1 2 20－10 2 ＝1 120(cm2)． 于是该实心零部件的表面积为 S＝S1＋S2＝1 300＋1 120＝2 420(cm2)， 故所需加工处理费为 0.2S＝0.2×2 420＝484(元)． 46．（2012·福建）如图 1－3 所示，在长方体 ABCD－A1B1C1D1 中，AB＝AD＝1，AA1＝2，M 为棱 DD1 上的一点． (1)求三棱锥 A－MCC1 的体积； (2)当 A1M＋MC 取得最小值时，求证：B1M⊥平面 MAC. 图 1－3 【答案】解：(1)由长方体 ABCD－A1B1C1D1 知， AD⊥平面 CDD1C1， ∴点 A 到平面 CDD1C1 的距离等于 AD＝1， 又 S △ MCC1＝1 2CC1×CD＝1 2×2×1＝1， ∴VA－MCC1＝1 3AD·S △ MCC1＝1 3. (2)将侧面 CDD1C1 绕 DD1 逆时针转 90°展开，与侧面 ADD1A1 共面(如图)， 当 A1，M，C 共线时，A1M＋MC 取得最小值． 由 AD＝CD＝1，AA1＝2，得 M 为 DD1 中点． 连接 C1M，在 △ C1MC 中，MC1＝ 2，MC＝ 2，CC1＝2. ∴CC21＝MC21＋MC2，得∠CMC1＝90°，即 CM⊥MC1. 又由长方体 ABCD－A1B1C1D1 知，B1C1⊥平面 CDD1C1，∴B1C1⊥CM. 又 B1C1∩C1M＝C1，∴CM⊥平面 B1C1M，得 CM⊥B1M； 同理可证，B1M⊥AM， 又 AM∩MC＝M，∴B1M⊥平面 MAC. 47．（2012·北京）如图 1－9(1)，在 Rt △ ABC 中，∠C＝90°，D，E 分别为 AC，AB 的中点，点 F 为线 段 CD 上的一点，将 △ ADE 沿 DE 折起到 △ A1DE 的位置，使 A1F⊥CD，如图 1－9(2)． (1)求证：DE∥平面 A1CB； (2)求证：A1F⊥BE； (3)线段 A1B 上是否存在点 Q，使 A1C⊥平面 DEQ？说明理由． 48．（2012·北京）某三棱锥的三视图如图 1－4 所示，该三棱锥的表面积是( ) 图 1－4 A．28＋6 5 B．30＋6 5 C．56＋12 5 D．60＋12 5 【答案】B 【解析】 本题考查三棱锥的三视图与表面积公式． 由三视图可知，几何体为一个侧面和底面垂直的三棱锥，如图所示，可知 S 底面＝1 2×5×4＝10， S 后＝1 2×5×4＝10， S 左＝1 2×6×2 5＝6 5， S 右＝1 2×4×5＝10， 所以 S 表＝10×3＋6 5＝30＋6 5. 49．（2012·安徽）某几何体的三视图如图 1－2 所示，则该几何体的体积等于________． 图 1－2 【答案】56 【解析】 如图，根据三视图还原的实物图为底面是直角梯形的直四棱柱，其体积为 V＝ Sh＝1 2 (2＋5)×4×4＝56. 50．（2012·全国）如图 1－1，四棱锥 P－ABCD 中，底面 ABCD 为菱形，PA⊥底面 ABCD，AC＝2 2， PA＝2，E 是 PC 上的一点，PE＝2EC. (1)证明：PC⊥平面 BED； (2)设二面角 A－PB－C 为 90°，求 PD 与平面 PBC 所成角的大小． 图 1－1 设 PD 与平面 PBC 所成的角为α，则 sinα＝ d PD ＝1 2. 所以 PD 与平面 PBC 所成的角为 30°. 方法二：(1)以 A 为坐标原点，射线 AC 为 x 轴的正半轴，建立如图所示的空间直角坐标系 A－xyz. 51．（2012·课标全国）如图 1－4，三棱柱 ABC－A1B1C1 中，侧棱垂直底面，∠ACB＝90°，AC＝BC＝1 2AA1， D 是棱 AA1 的中点． (1)证明：平面 BDC1⊥平面 BDC； (2)平面 BDC1 分此棱柱为两部分，求这两部分体积的比． 52．（2012·辽宁）如图 1－5，直三棱柱 ABC－A′B′C′，∠BAC＝90°，AB＝AC＝ 2，AA′＝1，点 M，N 分别 为 A′B 和 B′C′的中点． (1)证明：MN∥平面 A′ACC′； (2)求三棱锥 A′－MNC 的体积． (锥体体积公式 V＝1 3Sh，其中 S 为底面面积，h 为高) 图 1－5 【答案】解：(1)(证法一) 连结 AB′，AC′，由已知∠BAC＝90°， 53．（2012·辽宁）已知点 P，A，B，C，D 是球 O 表面上的点，PA⊥平面 ABCD，四边形 ABCD 是边长为 2 3的正方形，若 PA＝2 6，则 △ OAB 的面积为________． 图 1－4 54．（2012·课标全国）平面α截球 O 的球面所得圆的半径为 1，球心 O 到平面α的距离为 2，则此球的体积 为( ) A. 6π B．4 3π C．4 6π D．6 3π 【答案】B 【解析】 由题意，球的半径为 R＝ 12＋ 2 2＝ 3，所以球的体积为 V＝4 3πR3＝4 3π. 故选 B. 55．（2012·重庆）已知在直三棱柱 ABC－A1B1C1 中，AB＝4，AC＝BC＝3，D 为 AB 的中点． (1)求异面直线 CC1 和 AB 的距离； (2)若 AB1⊥A1C，求二面角 A1－CD－B1 的平面角的余弦值． 56．（2012·重庆）已知在直三棱柱 ABC－A1B1C1 中，AB＝4，AC＝BC＝3，D 为 AB 的中点． (1)求异面直线 CC1 和 AB 的距离； (2)若 AB1⊥A1C，求二面角 A1－CD－B1 的平面角的余弦值． 图 1－4 故DA1 → ＝(－2,0,2 2)，DB1 → ＝(2,0,2 2)，DC→ ＝(0，5，0)． 设平面 A1CD 的法向量为 m＝(x1，y1，z1)，则 m⊥DC→ ，m⊥DA1 → ，即 5y1＝0， －2x1＋2 2z1＝0， 取 z1＝1，得 m＝( 2，0,1)． 设平面 B1CD 的法向量为 n＝(x2，y2，z2)，则 n⊥DC→ ，n⊥DB1 → ，即 5y2＝0， 2x2＋2 2z2＝0， 取 z2＝－1，得 n＝( 2，0，－1)，所以 cos〈m，n〉＝ m·n |m|·|n| ＝ 2－1 2＋1· 2＋1 ＝1 3. 所以二面角 A1－CD－B1 的平面角的余弦值为1 3. 57．（2012·浙江）如图 1－5，在侧棱垂直底面的四棱柱 ABCD－A1B1C1D1 中，AD∥BC，AD⊥AB，AB ＝ 2，AD＝2，BC＝4，AA1＝2，E 是 DD1 的中点，F 是平面 B1C1E 与直线 AA1 的交点． (1)证明：(i)EF∥A1D1； (ii)BA1⊥平面 B1C1EF； (2)求 BC1 与平面 B1C1EF 所成的角的正弦值． 故 BA1⊥B1F， 所以 BA1⊥平面 B1C1EF. (2)设 BA1 与 B1F 交点为 H，连结 C1H. 由(1)知 BA1⊥平面 B1C1EF，所以∠BC1H 是 BC1 与面 B1C1EF 所成的角． 在矩形 AA1B1B 中，AB＝ 2，AA1＝2，得 BH＝ 4 6 . 在直角 △ BHC1 中，BC1＝2 5，BH＝ 4 6 ，得 sin∠BC1H＝BH BC1 ＝ 30 15 ， 所以 BC1 与平面 B1C1EF 所成角的正弦值是 30 15 . 58．（2012·天津）如图 1－4，在四棱锥 P－ABCD 中，底面 ABCD 是矩形，AD⊥PD，BC＝1，PC＝2 3， PD＝CD＝2. (1)求异面直线 PA 与 BC 所成角的正切值； (2)证明平面 PDC⊥平面 ABCD； (3)求直线 PB 与平面 ABCD 所成角的正弦值． 59．（2012·上海）如图 1－1，在三棱锥 P－ABC 中，PA⊥底面 ABC，D 是 PC 的中点，已知∠BAC＝π 2 ，AB ＝2，AC＝2 3，PA＝2，求： 图 1－1 (1)三棱锥 P－ABC 的体积； (2)异面直线 BC 与 AD 所成的角的大小(结果用反三角函数值表示)． 60．（2012·安徽）如图 1－3，长方体 ABCD－A1B1C1D1 中，底面 A1B1C1D1 是正方形，O 是 BD 的中点，E 是棱 AA1 上任意一点． (1)证明：BD⊥EC1； (2)如果 AB＝2，AE＝ 2，OE⊥EC1，求 AA1 的长． 图 1－3 61．（2012·全国）已知正四棱柱 ABCD－A1B1C1D1 中，AB＝2，CC1＝2 2，E 为 CC1 的中点，则直线 AC1 与平面 BED 的距离为( ) A．2 B. 3 C. 2 D．1 【答案】D 【解析】 本小题主要考查正四棱柱的性质以及直线到平面的距离的概念．解题的突破口 为直线到平面的距离的转化． 由已知可得 AC1＝4，取 AC 与 BD 的中点 O，连 OE，显然有 AC1∥OE 且平面 ACC1A1⊥平面 BED，∴ AC1 与平面 BED 的距离即为 AC1 与 OE 的距离，又∵AB＝2，CC1＝2 2，∴AC＝2 2，CC1＝AC，∴平面 AA1C1 为正方形，∴AC1 与平面 BED 的距离为 1 4CA1＝1，故选 D. 62．（2012·全国）已知正方体 ABCD－A1B1C1D1 中，E、F 分别为 BB1、CC1 的中点，那么异面直线 AE 与 D1F 所成角的余弦值为________． 63．（2012·全国）如图 1－1，四棱锥 P－ABCD 中，底面 ABCD 为菱形，PA⊥底面 ABCD，AC＝2 2，PA ＝2，E 是 PC 上的一点，PE＝2EC. (1)证明：PC⊥平面 BED； (2)设二面角 A－PB－C 为 90°，求 PD 与平面 PBC 所成角的大小． PC 与平面 BED 内两条相交直线 BD，EF 都垂直，所以 PC⊥平面 BED. (2)在平面 PAB 内过点 A 作 AG⊥PB，G 为垂足． 因为二面角 A－PB－C 为 90°，所以平面 PAB⊥平面 PBC. 即 2 2p－2r＝0 且 2p 3 ＋bq＋2 3r＝0， 令 p＝1，则 r＝ 2，q＝－ 2 b ，n＝ 1，－ 2 b ， 2 . 因为面 PAB⊥面 PBC，故 m·n＝0，即 b－2 b ＝0，故 b＝ 2，于是 n＝(1，－1， 2)，DP→ ＝(－ 2，－ 2， 2)， cos〈n，DP→ 〉＝ n·DP→ |n||DP→ | ＝1 2 ， 〈n，DP→ 〉＝60°. 因为 PD 与平面 PBC 所成的角和〈n，DP→ 〉互余， 故 PD 与平面 PBC 所成的角为 30°. 64．（2012·四川）下列命题正确的是( ) A．若两条直线和同一个平面所成的角相等，则这两条直线平行 B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 D．若两个平面都垂直于第三个平面，则这两个平面平行 65．（2012·四川）如图 1－3，半径为 R 的半球 O 的底面圆 O 在平面α内，过点 O 作平面α的垂线交半球面于 点 A，过圆 O 的直径 CD 作与平面α成 45°角的平面与半球面相交，所得交线上到平面α的距离最大的点为 B， 该交线上的一点 P 满足∠BOP＝60°，则 A、P 两点间的球面距离为( ) A．Rarccos 2 4 B.πR 4 C．Rarccos 3 3 D.πR 3 66．（2012·广东）如图 1－5 所示，在四棱锥 P－ABCD 中，AB⊥平面 PAD，AB∥CD，PD＝AD，E 是 PB 的中点，F 是 DC 上的点且 DF＝1 2AB，PH 为 △ PAD 中 AD 边上的高． (1)证明：PH⊥平面 ABCD； (2)若 PH＝1，AD＝ 2，FC＝1，求三棱锥 E－BCF 的体积； (3)证明：EF⊥平面 PAB. 67．（2012·福建）如图 1－3 所示，在长方体 ABCD－A1B1C1D1 中，AB＝AD＝1，AA1＝2，M 为棱 DD1 上的 一点． (1)求三棱锥 A－MCC1 的体积； (2)当 A1M＋MC 取得最小值时，求证：B1M⊥平面 MAC. 68．（2012·安徽）若四面体 ABCD 的三组对棱分别相等，即 AB＝CD，AC＝BD，AD＝BC，则________(写 出所有正确结论的编号)． ①四面体 ABCD 每组对棱相互垂直；②四面体 ABCD 每个面的面积相等；③从四面体 ABCD 每个顶点 出发的三条棱两两夹角之和大于 90°而小于 180°；④连接四面体 ABCD 每组对棱中点的线段相互垂直平分； ⑤从四面体 ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长． 69．（2012·四川）如图 1－5，在三棱锥 P－ABC 中，∠APB＝90°，∠PAB＝60°，AB＝BC＝CA，点 P 在平面 ABC 内的射影 O 在 AB 上． (1)求直线 PC 与平面 ABC 所成的角的大小； (2)求二面角 B－AP－C 的大小． 解法二： (1)设 AB 的中点为 D，连结 CD. 因为 O 在 AB 上，且 O 为 P 在平面 ABC 上的射影， 所以 PO⊥平面 ABC. 所以 PO⊥AB，且 PO⊥CD. 由 AB＝BC＝CA，知 CD⊥AB. 设 E 为 AC 中点，则 EO∥CD，从而 OE⊥PO，OE⊥AB. 如图，以 O 为坐标原点，OB、OE、OP 所在直线分别为 x、y、z 轴建立空间直角坐标系 O－xyz. 【2011 高考真题精选】 1.(2011 年高考安徽卷文科 8)一个空间几何体得三视图如图所示，则该几何体的表面积为 2．(2011 年高考广东卷文科 9)如图 1-3，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别为 等边三角形、等腰三角形和菱形，则该几何体体积为（ ） A． B． C． D． 2 【答案】C 【解析】由题得该几何体是如图所示的四棱锥 P-ABCD， ，棱锥的高， 3232322 1 3 13312332312 22  VPOhAO 所以选择 C. 3．（2011 年高考湖南卷文科 4)设图１是某几何体的三视图，则该 几何体的体积为 A．9 42  Ｂ．36 18  Ｃ． 9 122   Ｄ． 9 182   答案：D 解析：有三视图可知该几何体是一个长方体和球构成的组合体， 其体积 34 3 9+3 3 2= 183 2 2V     （ ） 。 4．（2011 年高考湖北卷文科 7)设球的体积为 V1,它的内接正方体的体积为 V2，下列说法中最合适的是 A. V1 比 V2 大约多一半 B. V1 比 V2 大约多两倍半 C. V1 比 V2 大约多一倍 D. V1 比 V2 大约多一倍半 答案：D 解析：设球半径为 R，其内接正方体棱长为 a，则 2 2 2 2a a a R   ，即 2 3 ,3a R 由 3 3 3 1 2 4 8, 33 9v R v a R   ，比较可得应选 D. 5.（2011 年高考山东卷文科 11)下图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱， 其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视 图、俯视图如下图．其中真命题的个数是 3 3 2 正视图 侧视图 俯视图 图 1 (A)3 (B)2 (C)1 (D)0 【答案】A 【解析】对于①,可以是放倒的三棱柱；容易判断②③可以. 6.（2011 年高考海南卷文科第 8 题）在一个几何体的三视图中，正视图和俯视图如右图，则相应的侧 视图可以为（ ） 7.（2011 年高考浙江卷文科 4)若直线l 不平行于平面 a ，且l a ，则 (A) a 内的所有直线与l 异面 (B) a 内不存在与l 平行的直线 (C) a 内存在唯一的直线与l 平行 (D) a 内的直线与l 都相交 【答案】 B 【解析】：直线 l 不平行于平面 a ，l a 所以l 与 a 相交，故选 B 8.（2011 年高考辽宁卷文科 8)一个正三棱柱的侧棱长和底面边长相等，体积为 2 3 ，它的三视图中的 俯视图如右图所示．左视图是一个矩形．则这个矩形的面积是 (A)4 (B) 2 3 (c)2 (D) 3 9.（2011 年高考全国卷文科 8)已知直二面角 l   ，点 , ,A AC l C  为垂足， , ,B BD l D  为 垂足，若 2, 1,AB AC BD   则 D 到平面 ABC 的距离等于 （A） 2 3 （B） 3 3 （C） 6 3 （D）1 10.（2011 年高考全国卷文科 12)已知平面 截一球面得圆 M，过圆心 M 且与 成 060 ，二面角的平面  截 该球面得圆 N，若该球的半径为 4，圆 M 的面积为 4 ，则圆 N 的面积为 (A) 7 (B)9 (c)11 (D)13 【答案】D 【解析】解：由圆 M 的面积为 4 得 2MA  ， 2 2 24 2 12OM    2 3OM  ，在 030Rt ONM OMN  中, 21 3, 3 132ON OM    2r= 4 13NS  圆 故选 D 11.（2011 年高考江西卷文科 9)将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左 视图为（ ） 【答案】D 【解析】左视图即是从正左方看，找特殊位置的可视点，连起来就可以得到答案. 12. （2011 年高考四川卷文科 6) 1l ， 2l ， 3l 是空间三条不同的直线，则下列命题正确的是 （A） 1 2 2 3,l l l l   1l // 2l （B） 1 2l l , 1l // 3l  1 3l l （C） 1l // 2l // 3l  1l ， 2l ， 3l 共面 （D） 1l ， 2l ， 3l 共点  1l ， 2l ， 3l 共面 答案：B 解析：若 1 2 2 3, ,l l l l  则 1 3,l l 有三种位置关系，可能平行、相交或异面，故 A 不对.虽然 1 2 3/ / / /l l l ， 或 1 2 3, ,l l l 共点，但是 1 2 3, ,l l l 可能共面，也可能不共面，故 C、D 也不正确. 13. （2011 年高考海南卷文科 16)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个 球面上.若圆锥底面面积是这个球面面积的 3 16 ,则这两个圆锥中,体积较小者的高与体积较大者的高的比值 为 . 【答案】 1 3 【解析】设圆锥的底面半径为 r ,球半径为 R ,则 2 23 416r R   ,解得 3 2r R ,所以对应球心距为 1 2 R ,故小圆锥的高为 1 1 2 2R R R  ,大圆锥的高为 3 2 R ,所以之比为 1 3 . 14. （2011 年高考福建卷文科 15)如图，正方体 ABCD-A1B1C1D1 中，AB=2。，点 E 为 AD 的中点，点 F 在 CD 上，若 EF∥平面 AB1C，则线段 EF 的长度等于_____________. 15. (2011 年高考天津卷文科 10)一个几何体的三视图如图所示(单位:m),则该几何体的体积为 3m . 【答案】4 【解析】由三视图知,该几何体是由上、下两个长方体组合而成的,容易求得体积为 4. 16．（2011 年高考湖南卷文科 19)（本题满分 12 分） 如图 3，在圆锥 PO 中，已知 2,PO O  的直径 2, ,AB C AB D AC  点 在 上,且 CAB=30 为 的中 点． （I）证明： ;AC POD 平面 （II）求直线和平面 PAC 所成角的正弦值． 17. (2011 年高考天津卷文科 17)（本小题满分 13 分） 如图,在四棱锥 P-ABCD 中,底面 ABCD 为平行四边形, 45ADC   ,AD=AC=1,O 为 AC 的中点,PO⊥平面 ABCD,PO=2, M 为 PD 的中点. (Ⅰ)证明 PB∥平面 ACM ; (Ⅱ)证明 AD⊥平面 PAC; (Ⅲ)求直线 AM 与平面 ABCD 所成角的正切值. 18. （2011 年高考福建卷文科 20)（本小题满分 12 分） 如图，四棱锥 P-ABCD 中，PA⊥底面 ABCD，AB⊥AD，点 E 在线段 AD 上，且 CE∥AB。 求证：CE⊥平面 PAD； （11）若 PA=AB=1，AD=3，CD= 2 ，∠CDA=45°，求四棱锥 P-ABCD 的体积 19 ．（2011 年高考陕西卷文科 16)（本小题满分 12 分）如图，在△ABC 中，∠ABC=45°， ∠BAC=90°，AD BC是 上的高 ，沿 AD 把是 BC 上的△ABD 折起， 使∠BDC=90°。（Ⅰ）证明：平面 ADB BDC 平面 ； （Ⅱ ）设 BD=1，求三棱锥 D— ABC 的表面积。 20. （2011 年高考湖北卷文科 18)如图，已知正三棱柱 1 1 1ABC A B C 的底面边长为 2，侧棱长为 3 2 ，点 E 在侧棱 1AA 上，点 F 在侧棱 1BB 上，且 2 2, 2AE BE  . (Ⅰ)求证： 1CF C (Ⅱ)求二面角 1EE CF C  的大小. 21.（2011 年高考浙江卷文科 20)（本题满分 14 分）如图，在三棱锥 P ABC 中，AB AC ，D 为 BC 的 中点， PO ⊥平面 ABC ，垂足O 落在线段 AD 上. 22.(2011 年高考江苏卷 16)如图，在四棱锥 ABCDP  中，平面 PAD⊥平面 ABCD，AB=AD，∠BAD=60°， E、F 分别是 AP、AD 的中点.求证： 23. (2011 年高考江苏卷 22)（本小题满分 10 分） 如图，在正四棱柱 1 1 1 1ABCD ABCD 中， 1 2, 1AA AB  ，点 N 是 BC 的中点，点 M 在 1CC 上，设二 面角 1A DN M  的大小为 。 （1）当 090  时，求 AM 的长； 22第 题图 （2）当 6cos 6   时，求CM 的长。 25.(2011 年高考安徽卷文科 19)（本小题满分 13 分） 如 图 ， ABCDEFG 为 多 面 体 ， 平 面 ABED 与 平 面 AGFD 垂 直 ， 点 O 在 线 段 AD 上 ， 1, 2,OA OD  OABV ,△OAC ，△ ODE ，△ODF 都是正三角形。 （Ⅰ）证明直线 BC ∥ EF ； （II）求棱锥 F-OBED 的体积。 26.（2011 年高考全国卷文科 20) (本小题满分 12 分)(注意：在试题卷上作答无效．．．．．．．．．) 如 图 ， 四 棱 锥 S ABCD 中 ， //AB CD , BC CD ， 侧 面 SAB 为 等 边 三 角 形 ， 2, 1AB BC CD SD    . （Ⅰ）证明： SD SAB 平面 ; （Ⅱ)求 AB 与平面 SBC 所成角的大小. 【2010 高考真题精选】 1.（2010 陕西文数） 8.若某空间几何体的三视图如图所示，则该几何体的体积是 （A）2 （B）1 （C） 2 3 （D） 1 3 【答案】B 【解析】本题考查立体图形三视图及体积公式 如图，该立体图形为直三棱柱 所以其体积为 12212 1  2.（2010 辽宁文数）（11）已知 , , ,S A B C 是球 O 表面上的点， SA ABC 平面 ， AB BC ， 1SA AB  ， 2BC  ，则球O 的表面积等于 （A）4 （B）3 （C）2 （D） 【答案】A. 【解析】由已知，球O 的直径为 2 2R SC  ，表面积为 24 4 .R  3.（2010 全国卷 2 文数）（11）与正方体 ABCD—A1B1C1D1 的三条棱 AB、CC1、A1D1 所在直线的距离 相等的点 （A）有且只有 1 个 （B）有且只有 2 个 （C）有且只有 3 个 （D）有无数个 4.（2010 全国卷 2 文数）（8）已知三棱锥 S ABC 中，底面 ABC 为边长等于 2 的等边三角形， SA 垂直于 底面 ABC ， SA =3，那么直线 AB 与平面 SBC 所成角的正弦值为 （A） 3 4 (B) 5 4 2 2 1 (C) 7 4 (D) 3 4 5.（2010 安徽文数）（9）一个几何体的三视图如图，该几何体的表面积是 （A）372 （B）360 （C）292 （D）280 【答案】B 【解析】该几何体由两个长方体组合而成，其表面积等于下面长方体的全面积加上面长方体的 4 个侧 面积之和。 2(10 8 10 2 8 2) 2(6 8 8 2) 360S            . 6.（2010 重庆文数）（9）到两互相垂直的异面直线的距离相等的点 （A）只有 1 个 （B）恰有 3 个 （C）恰有 4 个 （D）有无穷多个 【答案】D 【解析】放在正方体中研究,显然，线段 1OO 、EF、FG、GH、 HE 的中点到两垂直异面直线 AB、CD 的距离都相等， 所以排除 A、B、C，选 D 7.（2010 浙江文数）（8）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是 （A） 352 3 cm3 （B） 320 3 cm3 （C） 224 3 cm3 （D）160 3 cm3 【答案】B 【解析】本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算，属容易题。 8.（2010 福建文数）3．若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．等于 ( ) A B CD A1 B1 C1 D1 O A． 3 B．2 C． 2 3 D．6 【答案】D 【解析】由正视图知：三棱柱是以底面边长为 2，高为 1 的正三棱柱，所以底面积为 32 4 2 34    ，侧面积为3 2 1 6   ，选 D． 9.（2010 全国卷 1 文数）（12）已知在半径为 2 的球面上有 A、B、C、D 四点，若 AB=CD=2,则四面体 ABCD 的体积的最大值为 (A) 2 3 3 (B) 4 3 3 (C) 2 3 (D) 8 3 3 10.（2010 全国卷 1 文数）（9）正方体 ABCD - 1 1 1 1A B C D 中， 1BB 与平面 1ACD 所成角的余弦值为 （A） 2 3 （B） 3 3 （C） 2 3 （D） 6 3 【答案】D 【解析 1】因为 BB1//DD1,所以 B 1B 与平面 AC 1D 所成角和 DD1 与平面 AC 1D 所成角相等,设 DO⊥平面 AC 1D ，由等体积法得 1 1D ACD D ACDV V  ,即 1 1 1 1 3 3ACD ACDS DO S DD    .设 DD1=a, 则 1 2 2 1 1 1 3 3sin 60 ( 2 )2 2 2 2ACDS AC AD a a      , 21 1 2 2ACDS AD CD a   . 所以 1 3 1 2 3 33 ACD ACD S DD aDO aS a      ,记 DD1 与平面 AC 1D 所成角为 ,则 1 3sin 3 DO DD    ,所以 6cos 3   . 【解析 2】设上下底面的中心分别为 1 ,O O ； 1O O 与平面 AC 1D 所成角就是 B 1B 与平面 AC 1D 所成角， 1 1 1 1 3 6cos 1/ 32 O OO OD OD     11.（2010 全国卷 1 文数）(6)直三棱柱 1 1 1ABC A B C 中，若 90BAC   ， 1AB AC AA  ，则异 面直线 1BA 与 1AC 所成的角等于 (A)30° (B)45°(C)60° (D)90° 【答案】C 【解析】延长 CA 到 D，使得 AD AC ，则 1 1ADAC 为平行四边形， 1DA B 就是异面直线 1BA 与 1AC 所成的角，又三角形 1A DB 为等边三角形， 0 1 60DA B  12.（2010 四川文数）（12）半径为 R 的球O 的直径 AB 垂直于平面 a ，垂足为 B ， BCD 是平面 a 内 边长为 R 的正三角形，线段 AC 、 AD 分别与球面交于点 M 、 N ，那么 M 、 N 两点间的球面距离是 （A） 17arccos 25R （B） 18arccos 25R （C） 1 3 R （D） 4 15 R 【答案】A   A B   13.（2010 天津文数）（12）一个几何体的三视图如图所示，则这个几何体的体积为 。 14.（2010 四川文数）（15）如图，二面角 l   的大小是 60°，线段 AB  . B l ， AB 与l 所成的角为 30°.则 AB 与平面  所成的角的正弦值是 . 15.（2010 陕西文数）18.(本小题满分 12 分) 如图，在四棱锥 P—ABCD 中，底面 ABCD 是矩形 PA⊥平面 ABCD，AP=AB，BP=BC=2，E，F 分别是 PB,PC 的中点. (Ⅰ)证明：EF∥平面 PAD； (Ⅱ)求三棱锥 E—ABC 的体积 V. 解 (Ⅰ)在△PBC 中，E，F 分别是 PB，PC 的中点，∴EF∥BC. 又 BC∥AD,∴EF∥AD, 又∵AD  平面 PAD,EF  平面 PAD, ∴EF∥平面 PAD. (Ⅱ)连接 AE,AC,EC,过 E 作 EG∥PA 交 AB 于点 G, 则 BG⊥平面 ABCD,且 EG= 1 2 PA. 在△PAB 中，AD=AB,  PAB°,BP=2,∴AP=AB= 2 ,EG= 2 2 . ∴S△ABC= 1 2 AB·BC= 1 2 × 2 ×2= 2 , ∴VE-ABC= 1 3 S△ABC·EG= 1 3 × 2 × 2 2 = 1 3 . 【2009 高考真题精选】 1. (广东文 6 理 5)给定下列四个命题： ①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行； ②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行； ④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真 命题的是 Ａ．①和② Ｂ．②和③ Ｃ．.③和④ Ｄ．②和④ 答案：D 解析：①错, ②正确, ③错, ④正确.故选 D 2. (宁夏海南文 9 理 8) 如图，正方体 1 1 1 1ABCD A B C D 的棱线长为 1，线段 1 1B D 上有两个动点 E，F， 且 2 2EF  ，则下列结论中错误的是 （A） AC BE （B） / /EF ABCD平面 [来源:Zxxk.Com] （C）三棱锥 A BEF 的体积为定值 （D）异面直线 ,AE BF 所成的角为定值 解析：A 正确，易证 1 1 ;AC D DBB AC BE 平面 ，从而 B 显然正确， / / , / /EF BD EF ABCD 平面 易证；C 正确，可用等积法求得；D 错误。选 D. 3.(山东文理 4) 一空间几何体的三视图如图所示,则该几何体的体积为( ). A. 2 2 3  B. 4 2 3  C. 2 32 3   D. 2 34 3   解析：:该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为 1,高为 2,体积为 2 ,四棱锥的底面 边长为 2 ，高为 3 ，所以体积为  21 2 32 33 3    ，所以该几何体的体积为 2 32 3   . 答案：C 4.(辽宁文 5)如果把地球看成一个球体，则地球上的北纬 060 纬线长和赤道长的比值为 （A）0.8 （B）0.75 （C）0.5 （D）0.25 解析：设地球半径为 R,则北纬 060 纬线圆的半径为 Rcos60°＝ 1 2 R 而圆周长之比等于半径之比,故北纬 060 纬线长和赤道长的比值为 0.5. 答案：C 5. (浙江文 4)设 ,  是两个不同的平面，l 是一条直线，以下命题正确的是（ ） A．若 ,l     ，则l  B．若 / / , / /l    ，则 l  2 2 侧(左)视图 2 2 2 正(主)视图 C．若 , / /l    ，则l  D．若 / / ,l    ，则 l  答案：C 解析：此题主要考查立体几何的线面、面面的位置关系，通过对平行和垂直的考查，充分调动了立体 几何中的基本元素关系．对于 A、B、D 均可能出现 //l  ，而对于 C 是正确的． 6. (2009·安徽文 20) 本小题满分 13 分 如图，ABCD 的边长为 2 的正方形，直线l 与平面 ABCD 平行，E 和 F 式l 上的两个不同点，且 EA=ED， FB=FC, E 和 F是平面 ABCD 内的两点， EE 和 FF 都与平面 ABCD 垂直， （1）证明：直线 E F 垂直且平分线段 AD： （2）若∠EAD=∠EAB  060 ,EF 2,求多面 体 ABCDEF 的体积。 ∴ / 21 1 4 22 23 3 3E ABCD ABCDV S EE      正方形 又 / 21 1 1 2 22 23 3 2 3E BCF C BEF C BEA E ABC ABCV V V V S EE              ∴多面体 ABCDEF 的体积为 2 2E ABCD E BCFV V   。 7. (2009·福建文 20) （本小题满分 12 分） 如图，平行四边形 ABCD 中， 60DAB   ， 2, 4AB AD  将 CBD 沿 BD 折起到 EBD 的位置，使平面 EDB  平面 ABD （I）求证： AB DE （Ⅱ）求三棱锥 E ABD 的侧面积。 又 AB  平面 ,EBD BE  平面 ,EBD AB BE  14, 42ABEBE BC AD S AB BE       ,DE BD 平面 EBD  平面 ABD ED  ，平面 ABD 而 AD  平面 1, , 42ADEABD ED AD S AD DE      综上，三棱锥 E ABD 的侧面积， 8 2 3S   8. (2009·广东文 17)（本小题满分 13 分） 某高速公路收费站入口处的安全标识墩如图 4 所示,墩的上半部分是正四棱锥 P－EFGH,下半部分是长 方体 ABCD－EFGH.图 5、图 6 分别是该标识墩的正(主)视图和俯视图. （1）请画出该安全标识墩的侧(左)视图; （2）求该安全标识墩的体积 （3）证明:直线 BD  平面 PEG （２）该安全标识墩的体积为： P EFGH ABCD EFGHV V V   2 21 40 60 40 20 32000 32000 640003          2cm （３）如图,连结 EG,HF 及 BD，EG 与 HF 相交于 O,连结 PO.由正四棱锥的性质可知, PO  平面 EFGH , PO HF  又 EG HF HF  平面 PEG 又 BD HFP BD  平面 PEG； 9. (2009·辽宁文 19)（本小题满分 12 分） 如图，已知两个正方形 ABCD 和 DCEF 不在同一平面内，M，N 分别为 AB，DF 的中点。 （I）若 CD＝2，平面 ABCD ⊥平面 DCEF，求直线 MN 的长； （II）用反证法证明：直线 ME 与 BN 是两条异面直线。 【解析】解： （Ⅰ）取 CD 的中点 G 连结 MG，NG. 因为 ABCD，DCEF 为正方形，且边长为 2， B A N D C E F M G 10. (2009·宁夏海南文 19) （18）（本小题满分 12 分） 如图，在三棱锥 P ABC 中，⊿ PAB 是等边三角形，∠PAC=∠PBC=90 º （Ⅰ）证明：AB⊥PC （Ⅱ）若 4PC  ，且平面 PAC ⊥平面 PBC ， 求三棱锥 P ABC 体积。 【解析】解： （Ⅰ）因为 PAB 是等边三角形， 90PAC PBC     , 所以 Rt PBC Rt PAC   ,可得 AC BC 。 如图，取 AB 中点 D ，连结 PD ,CD , 则 PD AB ,CD AB , 所以 AB  平面 PDC , P A B C 12.（2009·山东文 18）（（本小题满分 12 分） 如图，在直四棱柱 ABCD-A 1 B 1 C 1 D 1 中，底面 ABCD 为等腰梯形，AB//CD，AB=4, BC=CD=2, AA 1 =2, E、E 1 分别是棱 AD、AA 1 的中点. 设 F 是棱 AB 的中点,证明：直线 EE 1 //平面 FCC 1 ； 证明:平面 D1AC⊥平面 BB1C1C. 【解析】证明:（1）在直四棱柱 ABCD-A 1 B 1 C 1 D 1 中，取 A1B1 的中点 F1， 连接 A1D，C1F1，CF1，因为 AB=4, CD=2,且 AB//CD， 所以 CDA1F1，A1F1CD 为平行四边形，所以 CF1//A1D， 又因为 E、E 1 分别是棱 AD、AA 1 的中点，所以 EE1//A1D， 所以 CF1//EE1，又因为 1EE  平面 FCC 1 ， 1CF  平面 FCC 1 ， E A B C F E1 A1 B1 C1D1 D F1 E A B C F E1 A1 B1 C1D1 D 所以直线 EE 1 //平面 FCC 1 . （2）连接 AC,在直棱柱中，CC1⊥平面 ABCD,AC  平面 ABCD, 所以 CC1⊥AC,因为底面 ABCD 为等腰梯形，AB=4, BC=2, F 是棱 AB 的中点,所以 CF=CB=BF， △ BCF 为正三角形， 60BCF  , △ ACF 为等腰三角形，且 30ACF   所以 AC⊥BC, 又因为 BC 与 CC1 都在平面 BB1C1C 内且交于点 C, 所以 AC⊥平面 BB1C1C,而 AC  平面 D1AC, 所以平面 D1AC⊥平面 BB1C1C. 13 ． (2009· 浙 江 文 19) （ 本 题 满 分 14 分 ） 如 图 ， DC  平 面 ABC ， / /EB DC ， 2 2AC BC EB DC    ， 120ACB   ， ,P Q 分别为 ,AE AB 的中点． （I）证明： / /PQ 平面 ACD ；（II）求 AD 与平面 ABE 所成角的正弦值． E A B C F E1 A1 B1 C1D1 D 22 所以 5 5 5 1sin  AD DPDAP 14．（2009·天津文理 19）（本小题满分 12 分） 如图，在五面体 ABCDEF 中，FA  平面 ABCD, AD//BC//FE ，AB  AD ，M 为 EC 的中点， AF=AB=BC=FE= 1 2 AD (I) 求异面直线 BF 与 DE 所成的角的大小； (II) 证明平面 AMD  平面 CDE； （III）求二面角 A-CD-E 的余弦值。 （II）证明：因为 .CEMPMP.CEDMCEM  ，则连结的中点，所以为且DEDC .CDEAMDCDECE.AMDCEMDMMP 平面，所以平面平面而平面，故又  （III） 因为，所以因为，的中点，连结为解：设 .CDEQDECE.EQPQCDQ  .ECDAEQPCDPQPDPC 的平面角为二面角，故，所以  由（I）可得， .2 2 2 6EQ aPQaPQEP  ，， ，中，于是在 3 3cosEPQRt  EQ PQEQP [来源:学科网] 方法二：如图所示，建立空间直角坐标系， 点 A 为坐标原点。设 ，1AB 依题意得  ，，，001B  ，，，011C  ，，，020D  ，，，110E  ，，，100F .2 112 1M      ，， （I）  ，，，解： 101BF   ，，， 110DE  .2 1 22 100 DEBF DEBFDEcos   ，于是 BF 所以异面直线 BF 与 DE 所成的角的大小为 060 . （II）证明： ，，，由      2 112 1AM  ，，，101CE    0AMCE020AD  ，可得，， ， .AMDCEAADAM.ADCEAMCE.0ADCE 平面，故又，因此，   .CDEAMDCDECE 平面，所以平面平面而  （III）      .0D 0)(CDE Eu CEuzyxu ，，则，，的法向量为解：设平面 .111(1.0 0 ），，，可得令，于是       uxzy zx 又由题设，平面 ACD 的一个法向量为 ).100( ，，v .3 3 13 100cos    vu vuvu，所以， 【2008 年高考真题精选】 1.（2008·海南、宁夏文科卷）一个六棱柱的底面是正六边形，其侧棱垂直底面。已知该六棱柱的顶点 都在同一个球面上，且该六棱柱的高为 3 ，底面周长为 3，那么这个球的体积为 _________ 解析：∵正六边形周长为３，得边长为 1 2 ，故其主对角线为１，从而球的直径  2 22 3 1 2R    ∴ 1R  ∴球的体积 4 3V   答案： 4 3  2.（2008·海南、宁夏文科卷）已知平面α⊥平面β，α∩β= l，点 A∈α，Al，直线 AB∥l，直线 AC⊥l， 直线 m∥α，m∥β，则下列四种位置关系中，不一定．．．成立的是（ ） A. AB∥m B. AC⊥m C. AB∥β D. AC⊥β 解析：容易判断Ａ、Ｂ、Ｃ三个答案都是正确的，对于Ｄ，虽然 AC l ，但ＡＣ不一定在平面  内， 故它可以与平面 相交、平行，故不一定垂直； 答案：D 3．（2008·广东文科卷）如图 5 所示，四棱锥 P-ABCD 的底面 ABCD 是半径为 R 的圆的内接四边形，其 中 BD 是圆的直径， 60 , 45 , ~ABD BDC ADP BAD       。 （1）求线段 PD 的长； （2）若 11PC R ，求三棱锥 P-ABC 的体积。 4．（2008·山东文科卷）如图，在四棱锥 P ABCD 中，平面 PAD  平面 ABCD ，AB DC∥ ， PAD△ 是 等边三角形，已知 2 8BD AD  ， 2 4 5AB DC  ． （Ⅰ）设 M 是 PC 上的一点，证明：平面 MBD  平面 PAD ； （Ⅱ）求四棱锥 P ABCD 的体积． 解析：（Ⅰ）证明：在 ABD△ 中， 由于 4AD  ， 8BD  ， 4 5AB  ， A B C M P D 所以 2 2 2AD BD AB  ． 【最新模拟】 1．（2013·韶关模拟）三棱柱的直观图和三视图(正视图和俯视图是正方形，侧视图是等腰直角三角形) 如图 K27－3 所示，则这个三棱柱的全面积等于( ) 图 K27－3 A．12＋4 2 B．6＋2 2 C．8＋4 2 D．4 【答案】A 【解析】 由三视图的数据可知，三棱柱的全面积为 S＝2×1 2×2×2＋(2＋2＋2 2)×2＝12＋4 2，选 A. 2．（2013·辽宁模拟）已知球的直径 SC＝4，A，B 是球面上的两点，AB＝2，∠BSC＝∠ASC＝45°，则 棱锥 S－ABC 的体积是( ) A. 3 3 B.2 3 3 C.4 3 3 D.5 3 3 3．（2013·江西模拟）已知α、β是不同的平面，m、n 是不同的直线，给出下列命题： ①若 m⊥α，m ⊂ β，则α⊥β； ②若 m ⊂ α，m ⊂ β，n∥β，m∥β，则α∥β； ③如果 m ⊂ α，n ⊄ α，m、n 是异面直线，那么 n 与α相交； ④若α∩β＝m，n∥m，且 n ⊄ α，n ⊄ β，则 n∥α且 n∥β. 其中正确命题的个数是( ) A．1 B．2 C．3 D．4 4．（2013·衡水中学模拟）四棱锥 P－ABCD 的顶点 P 在底面 ABCD 上的投影恰好是 A，其正视图与侧视图 都是腰长为 a 的等腰直角三角形．则在四棱锥 P－ABCD 的任意两个顶点的连线中，互相垂直的异面直线共 有________对． 【答案】5 【解析】 四棱锥 P－ABCD，如图，互相垂直的异面直线有 PA 与 BC，CD，BD；AD 与 PB，PC；共 5 对． 5．（2013·哈尔滨模拟）正方体 ABCD－A1B1C1D1 的棱长为 1，点 M 为 D1C1 上的点，且 D1M∶MC1＝3∶ 1，则 CM 和平面 AB1D1 所成角的大小是θ，则 sinθ等于( ) A.1 2 B. 3 2 C.5 53 53 D.5 51 51 【答案】D 【解析】 易证 CA1⊥D1B1，CA1⊥D1A，CA1⊥平面 AB1D1，所以 CM 和平面 AB1D1 所成角 θ是∠A1CM 的余角， 则 sinθ＝cos∠A1CM＝A1C2＋CM2－A1M2 2A1C·CM ， A1C＝ 3，CM＝ 17 4 ，A1M＝5 4 ， ∴sinθ＝cos∠A1CM＝A1C2＋CM2－A1M2 2A1C·CM ＝5 51 51 . 6．（2013·辽宁模拟）棱长为 1 的正方体和它的外接球被一个平面所截，截面是一个圆及其内接正三角 形，那么球心到截面的距离等于________． 7．（2013·山东模拟）如图 G8－5，已知四棱锥 P－ABCD 中，底面 ABCD 是直角梯形，AB∥CD，∠ABC＝ 45°，DC＝1，AB＝2，PA⊥平面 ABCD，PA＝1. (1)求证：AB∥平面 PCD； (2)求证：BC⊥平面 PAC； (3)若 M 是 PC 的中点，求三棱锥 M－ACD 的体积． 8【天津市新华中学 2013 届高三上学期第三次月考数学试卷】设 ba, 是两条直线， , 是两个平面，则 ba  的一个充分条件是 ( ) A.   ,//,ba B.  //,,  ba C.  //,,  ba D.   ,//,ba 【答案】C 【解析】若b  ， / /  ，所以b  ，又 a  ，所以b a ，即 a b ，所以选 C. 9.【山东省济宁市 2013 届高三上学期期末考试文】下列命题中错．误．的是 A.如果平面  平面  ，那么平面 内一定存在直线平行于平面  B.如果平面 不垂直于平面  ，那么平面 内一定不存在直线垂直于平面  C.如果平面  平面 ，平面  平面 ， l   ，那么直线l  平面 D.如果平面   平面  ，那么平面 内所有直线都垂直于平面  【答案】D 【 解析】根据面面垂直的的性质可知，D 错误。 10.【2013 届贵州天柱民中、锦屏中学、黎平一中、黄平民中四校联考】一个平面图形的面积为 S ，其 直观图的面积为 S ，则 S S  （ ） A． 2 2 B． 2 C． 2 D．1 【答案】A 【解析】直观图在底不变的情况下，高变为原来的 1 sin2 4  倍。设平面图形的高为 h ，直观图的高为 'h ， 则有 1 2' sin2 4 4h h h   ，即 2 2 'h h ，所以 : ' 2 2S S h h   ，选 A. 11.【2013 届贵州天柱民中、锦屏中学、黎平一中、黄平民中四校联考】若 , ,a b c 是空间三条不同的直 线， ,  是空间中不同的平面，则下列命题中不正确的是（ ） A．若 c  ， c  ，则 //  B．若 b  ， b  ，则  C．当 ,b a   且 c 是 a 在 内的射影，若 b c ，则 a b D．当 b  且 c  时，若 //c  ，则 //b c 【答案】D 【解析】选项中，当 //c  ，若 b c， 共面，则有 //b c ，若b c， 不共面，则 //b c 不成立，所以选 D. 12.【2013 年山东省临沂市高三教学质量检测考试】具有如图所示的正视图和俯视图的几何体中，体积 最大的几何体的表面积为 (A) 3 (B)7+3 2 (C) 7 2  (D)14 【答案】D 【解析】由正视图和俯视图可知，该几何体可能是四棱柱或者是水平放置的三棱柱，或水平放置的圆 柱 . 由 图 象 可 知 四 棱 柱 的 体 积 最 大 。 四 棱 柱 的 高 为 1 ， 底 面 边 长 分 别 为 1,3 ， 所 以 表 面 积 为 2(1 3 1 1 3 1) 14      ，选 D. 13.【2013 河北省名校名师俱乐部高三 3 月模拟考试】如图是一个几何体的三视图，则这个几何体的体 积是（ ） A．26 B．27 C． 57 2 D．28 【答案】C 【解析】根据三视图知，该几何体由棱长为 3 的正方体和底面积为 9 2 ，高为 1 的三棱锥组成，所以其 体积 2 3 1 3 573 13 2 2V      14.【广东省揭阳市 2013 届高三 3 月第一次高考模拟】一简单组合体的三视图及尺寸如图( 1)示（单位: ） 则该组合体的体积为．[来源:学科网] A. 72000 B. 64000 C. 56000 D. 44000 【答案】B 【解析】由三视图知，该组合体由两个直棱柱组合而成，故其体积 ，故选 B. 15.【广西百所高中 2013 届高三年级第三届联考】如图，三棱锥 P—ABC 中， PA  平面 ABC，PA=2， ABC 是边长为 3 的正三角形，点 D 是 PB 的中点，则异面直线 PA 与 CD 所成角的正切值为（ ） A． 2 3 B． 3 2 C． 1 3 D． 1 2 【答案】B 【解析】取 AB 的中点 E，连结 CE，DE，则 CDE 为 PA 与 CD 所成的角，由已知得 DE ABC ， DE=1， 3 2CE  ，∴ 3tan 2 CECDE DE    16.【山东省济宁市 2013 届高三上学期期末考试】若某空间几何体的三视图如图所示，则该几何体的体 积是 A. 1 3 B. 2 3 C.1 D.2 【答案】C 【解析】由三视图可知该几何体是放倒的三棱柱，三棱柱的高为 2 ，三角形的两直角边分 别为1, 2 ，所以三棱柱的体积为 1 1 2 2 12     ，选 C. 17.【山东省济宁市 2013 届高三上学期期末考试文】.已知一个空间几何体的三视图如图所示，其中正 视图、侧视图都是由半圆和矩形组成，根据图中标出的尺寸，可得这个几何体的体积是 . 【答案】 5 3  【解析】由三视图可知，该几何体的上面是个半球，球半径为 1，下面是个圆柱，底面半 径为 1，圆柱的高为 1.所以该几何体的体积为 1 4 5 2 3 3     。 18 【上海市普陀 2013 届高三一模】三棱锥 S-ABC 中，E、F、G、H 分别为 SA、AC、BC、SB 的中点，则截面 EFGH 将三棱锥 S-ABC 分成两部分的体积之比为 . 【答案】1:1 【解析】取 AB 中点 I，连 HI、GI，则 EFA-HGI 是三棱柱，由于 I 是 AB 中点，∴B 与 A 到面 HGI 的距 离相等，∴VEFA-HGI =3VB-HGI，而 VB-HGI:VB-SAC=1:23=1:8，令 VB-HGI=1，则 VEFA-HGI =3， ∴VB-HGI+ VEFA-HGI =4，故分成两部分的体积之比为为 1:1. 19.【2013 年石家庄市高中毕业班复习教学质量检测（二）】 如图，已知三棱柱 ABC-A1B1C1 (I)若 M、N 分别是 AB，A1C 的中点，求证：MN//平面 BCC1B1 (II)若三棱柱 ABC－A1B1C1 的各棱长均为 2，∠B1BA＝∠B1BC＝60°，P 为线段 B1B 上的动点，当 PA ＋PC 最小时，求证：B1B⊥平面 APC。 【解析】（Ⅰ）证明：连接 则 ,因为 AM=MB,所以 MN ……………3 分 又 , 所以 MN// .…………5 分 （Ⅱ）将平面 展开到与平面 共面, 到 的位置，此时 为菱形，…………7 分 可知 即为 的最小值，…………9 分 此时， , A B C A B  C  FE 所以 , ，即 ， ， 所以， .……………12 分 20. 【湖北省八校 2013 届高三第二次联考】（本小题满分 12 分）如图直三棱柱 ABC A B C   的侧棱长为 3， AB BC ，且 3AB BC  ，点 ,E F 分别是棱 ,AB BC 上的动点，且 AE BF . (Ⅰ)求证：无论 E 在何处，总有 CB C E  ； (Ⅱ)当三棱锥 B EB F 的体积取得最大值时，求异面直线 A F 与 AC 所成角的余弦值. 3 5 2AF A E  ， 9 2A F  ， 2cos 2   A FE ……12 分 21 【天津市新华中学 2012 届高三上学期第二次月考文】如图， PAD 为等边三角形，ABCD 为矩形， 平面 PAD 平面 ABCD ， 2AB ， E 、 F 、G 分别为 PA 、 BC 、 PD 中点， 22AD 。 （1）求 PB 与平面 ABCD 所成角； （2）求证： EFAG  ； （3）求多面体 AGFP  的体积。 【答案】解：（1）取 AD 中点 M ，连 PM 、 FM ∵平面 PAD 平面 ABCD，交线为 AD ∵正 PAD ∵ ADPM   PM 平面 ABCD PBM 即为所求。 6222 3 PM 6MB  45PBM （2）∵正 PAD ∵G 是 PD 中点 PDGA  PDEM // MEAG  ∵平面 PAD 平面 ABCD，交线为 AD ADMF   MF 平面 PAD AG 平面 PAD AGMF  MMFEM   AG 平面 EMF EFAG  （3）   23 1 3 1 AGPAGPFAGFP SMFVV 3 32622 1  6AG 6GC 32AC ACAG  EFAC // 22.【云南省玉溪一中 2013 届高三第四次月考文】（本小题满分 12 分） 如图所示，在棱长为 2 的正方 体 1 1 1 1ABCD A B C D 中， E 、 F 分别为 1DD 、 DB 的中点．