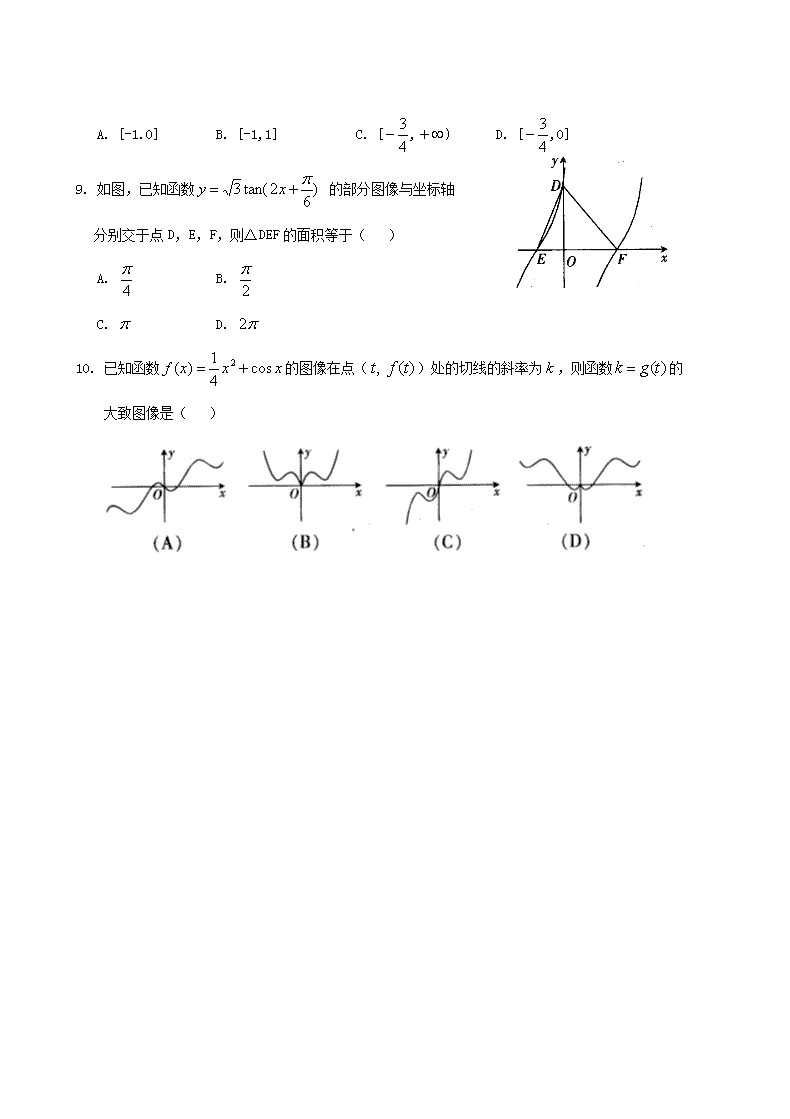宁夏银川唐徕回民中学2020届高三下学期第三次模拟考试数学（理）试题 15页

银川唐徕回民中学 ‎2020届高三年级第三次模拟考试 理 科 数 学 考生作答时，将答案答在答题卡上，在本试卷上答题无效。考试结束后，将本试卷和答题卡一并交回。‎ 注意事项：‎ ‎ 1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。‎ ‎ 2．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答题时使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。‎ ‎ 3．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效。‎ ‎ 4．保持卡面清洁，不折叠，不破损。‎ ‎ 5．做选考题时，考生按照题目要求作答，并用2B铅笔在答题卡上把所选题目对应的题号涂黑。‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，共60分。在每小题列出的四个选项中，‎ 选出符合题目要求的一项。‎ ‎1．已知集合M={}，N={}，则M∩N=（ ）‎ ‎ A. [] B. (] C. [] D. ()‎ ‎2. 若复数表示的点在虚轴上，则实数的值是（ ）‎ ‎ A. -1 B. +4 C. +4和-1 D. -1和6‎ ‎3. 下列说法正确的个数为（ ）‎ ‎ ①若，则 ②若，，则 ‎③若，，则 ④若，，则 A. ‎4 B. 3 C. 2 D. 1‎ 4. 已知圆截直线所得的弦长为，则=（ ）‎ A. ‎ B. C. D. 2‎ 5. 已知是平面外的两条不同直线，给出下列三个论断：‎ ‎ ① ② ③‎ ‎ 以其中的两个论断作为条件，余下的一个论断作为结论，则其可以构成______个正确命题.‎ A. ‎0 B. 1 C. 2 D. 3‎ 6. 某示范农场的鱼塘放养鱼苗8万条，根据这几年的经验，鱼苗的成活率为95%，一段时间后准 备打捞出售，第一网捞出40条，称得平均每条鱼2.5kg；第二网捞出25条，称得平均每条鱼 ‎3kg；第三网捞出35条，称得平均每条鱼2kg，则估计鱼塘中鱼的总质量为（ ）‎ A. ‎186200kg B. 196000kg C. 190000kg D. 186250kg 7. 在△ABC中，内角A，B，C所对的边长分别为，若A，B=，C=1，则△ABC 的面积为（ ）‎ A. ‎ B. C. D. ‎ 8. 在边长为2的等边三角形ABC中，若D是BC边上的中点，点P是线段AD上的一动点，则 ‎·的取值范围是（ ）‎ A. ‎[-1.0] B. [-1,1] C. [,) D. [,0]‎ 4. 如图，已知函数 的部分图像与坐标轴 分别交于点D，E，F，则△DEF的面积等于（ ）‎ A. ‎ B. ‎ C. D. ‎ 5. 已知函数的图像在点（）处的切线的斜率为，则函数的 大致图像是（ ）‎ ‎ ‎ 4. 已知三棱锥D—ABC四个顶点均在半径为R的球面上，且AB=BC=，AC=2，若该三棱锥体积 的最大值为1，则这个球的表面积为（ ）‎ A. ‎ B. C. D. ‎ 5. 已知F1，F2是椭圆C：（）的左、右焦点，A 是C的左顶点，点P在过 A且斜率为的直线上，△PF1F2为等腰三角形，∠F1F2P=1200，则C的离心率为（ ）‎ A. ‎ B. C. D. ‎ 第Ⅱ卷 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13. 已知双曲线C：的焦距为，则C的离心率为 .‎ ‎14. 已知，(0，），则= .‎ ‎15. 《无字证明》就是将数学命题和简单、有创意而且易于理解的几何图形呈现出来。请根据右图写出该图所验证的一个三角恒等变换公式： .‎ ‎16. 阅读下列材料，回答所提问题：‎ 设函数，①的定义域为R，其图像是一条连续不断的曲线；②是偶函数；③在（0，）上不是单调函数；④恰有2个零点.‎ 写出符合上述①②④条件的一个函数的解析式是 ；写出符合上述所有条件的一个函数的解析式是 .‎ 三、解答题（共70分。解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分12分）‎ 已知公差不为零的等差数列的前项和为，且=1，是与的等比中项.‎ （1） 求数列的通项公式；‎ （2） 在①；②（）中选一个条件使数列是等比数列，并说明理由，并求出数列的前项和.‎ ‎18．（本小题满分12分）‎ 在正方体ABCD—A1B1C1D1中，已知E，F，G分别CC1，BC，CD的中点，‎ ‎（1）求证：AB1//GE；‎ ‎（2）求证：A1G⊥平面EFD；‎ ‎（3）求二面角B—A1C—D的余弦值.‎ ‎19.（本小题满分12分）‎ 已知直线与抛物线C：交于M，N两点，点Q为线段MN的中点；‎ （1） 若直线经过抛物线C的焦点，且，求点Q的横坐标；‎ （2） 若，设直线的方程为，求点Q的横坐标的最 小值，并求此时直线的方程.‎ ‎20.（本小题满分12分）‎ 有甲、乙两家公司都需要招聘求职者，这两家公司的聘用信息如下：‎ （1） 根据以上信息，如果你是该求职者，你会选择哪一家？说明理由.‎ （2） 某课外实习作业小组调查了1000名职场人士，就选择这两家公司的意愿做了统计，得到以下数据分布：‎ 若分析选择意愿与年龄这两个分类变量，计算得到的的观测值为=5.5513，则得出“选择意愿与年龄有关系”的结论犯错误的的概率的上限是多少？并用统计学知识分析，选择意愿与年龄变量和性别变量哪一个关联性更大.‎ ‎21．（本小题满分12分）‎ ‎ 已知函数，‎ （1） 当时，求证：函数存在唯一极值点；‎ （2） 若，，求证：函数在（0，）上有唯一零点.‎ 请考生在第22、23两题中任选一题做答，如果多做，则按所做的第一题记分，答时用2B铅笔在答题卡上把所选题目的题号涂黑.‎ ‎22．（10分）选修4-4：坐标系与参数方程 在平面直角坐标系中，曲线C的参数方程为（为参数），以原点O为极点，轴的正半轴为极轴且取相同的单位长度建立极坐标.‎ （1） 求曲线C的极坐标方程；‎ （2） 在极坐标系中，M，N是曲线C上的两点，若∠MON=，求｜OM|+｜ON|的最大值.‎ ‎23．（10分）选修4-5：不等式选讲 已知定义在R上的函数，‎ （1） 若的最大值为3，求实数的值；‎ 若，求实数的取值范围. ‎ 高三理科数学三模参考答案