2020届二轮复习同角三角函数基本关系式与诱导公式课件（25张）（全国通用） 25页

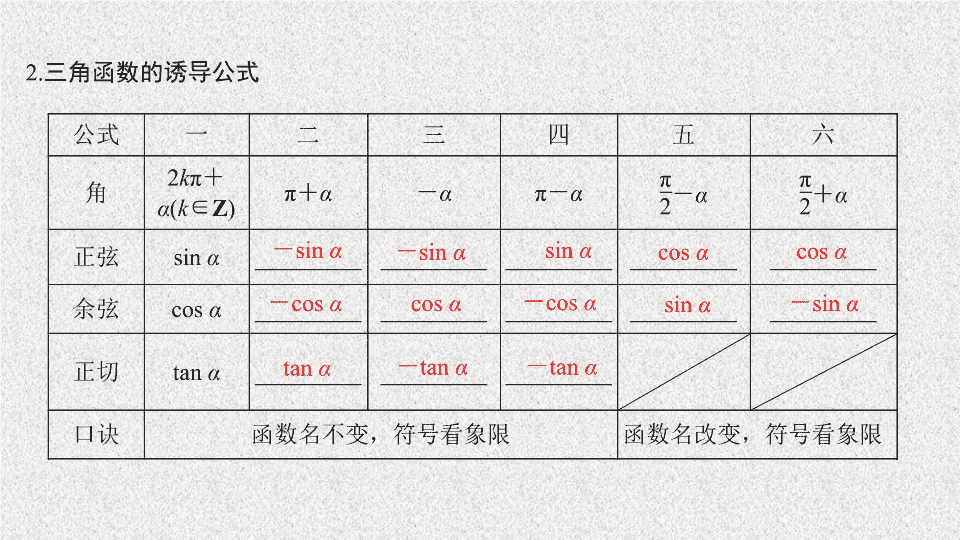
知 识 梳 理 1. 同角三角函数的基本关系 (1) 平方关系： ________________. sin 2 α ＋ cos 2 α ＝ 1 2. 三角函数的诱导公式 － sin α － sin α sin α cos α cos α － cos α cos α － cos α sin α － sin α t an α － tan α － tan α [ 微点提醒 ] 1. 同角三角函数关系式的常用变形 (sin α ±cos α ) 2 ＝ 1±2sin α cos α ； sin α ＝ tan α ·cos α . 2. 诱导公式的记忆口诀 3. 在利用同角三角函数的平方关系时，若开方，要特别注意判断符号 . 基 础 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) (1)sin(π ＋ α ) ＝－ sin α 成立的条件是 α 为锐角 .( 　　 ) (2) 六组诱导公式中的角 α 可以是任意角 .( 　　 ) 解析　 (1) 中对于任意 α ∈ R ，恒有 sin(π ＋ α ) ＝－ sin α . (3) 中当 α 的终边落在 y 轴上，商数关系不成立 . 答案 　 (1) × 　 (2) √ 　 (3) × 　 (4) × 2. ( 必修 4P115 练习 1T4 改编 ) 已知 tan α ＝－ 3 ，则 cos 2 α － sin 2 α ＝ ( 　　 ) 答案　 B 答案 　 A 答案　 A 答案　 D 答案　 1 考点一　同角三角函数基本关系式的应用 ∴ cos α <0 ， sin α <0 且 cos α >sin α ， ∴ cos α － sin α >0. 答案　 (1)B 　 (2)A 2. 应用公式时注意方程思想的应用：对于 sin α ＋ cos α ， sin α cos α ， sin α － cos α 这三个式子，利用 (sin α ±cos α ) 2 ＝ 1±2sin α cos α ，可以知一求二 . 3. 注意公式逆用及变形应用： 1 ＝ sin 2 α ＋ cos 2 α ， sin 2 α ＝ 1 － cos 2 α ， cos 2 α ＝ 1 － sin 2 α . 考点二　诱导公式的应用 规律方法 　 1. 诱导公式的两个应用 (1) 求值：负化正，大化小，化到锐角为终了 . (2) 化简：统一角，统一名，同角名少为终了 . 2. 含 2π 整数倍的诱导公式的应用 由终边相同的角的关系可知，在计算含有 2π 的整数倍的三角函数式中可直接将 2π 的整数倍去掉后再进行运算，如 cos(5π － α ) ＝ cos(π － α ) ＝－ cos α . 考点三　同角三角函数基本关系式与诱导公式的活用 ∴ sin α ＝ 3cos α ，代入 sin 2 α ＋ cos 2 α ＝ 1 ， 答案　 (1)A 　 (2)C 规律方法 　 1. 利用同角三角函数关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形 . 2.(1) 注意角的范围对三角函数值符号的影响，开方时先判断三角函数值的符号； [ 思维升华 ] 1 . 同角三角函数基本关系可用于统一函数；诱导公式主要用于统一角，其主要作用是进行三角函数的求值、化简和证明 .