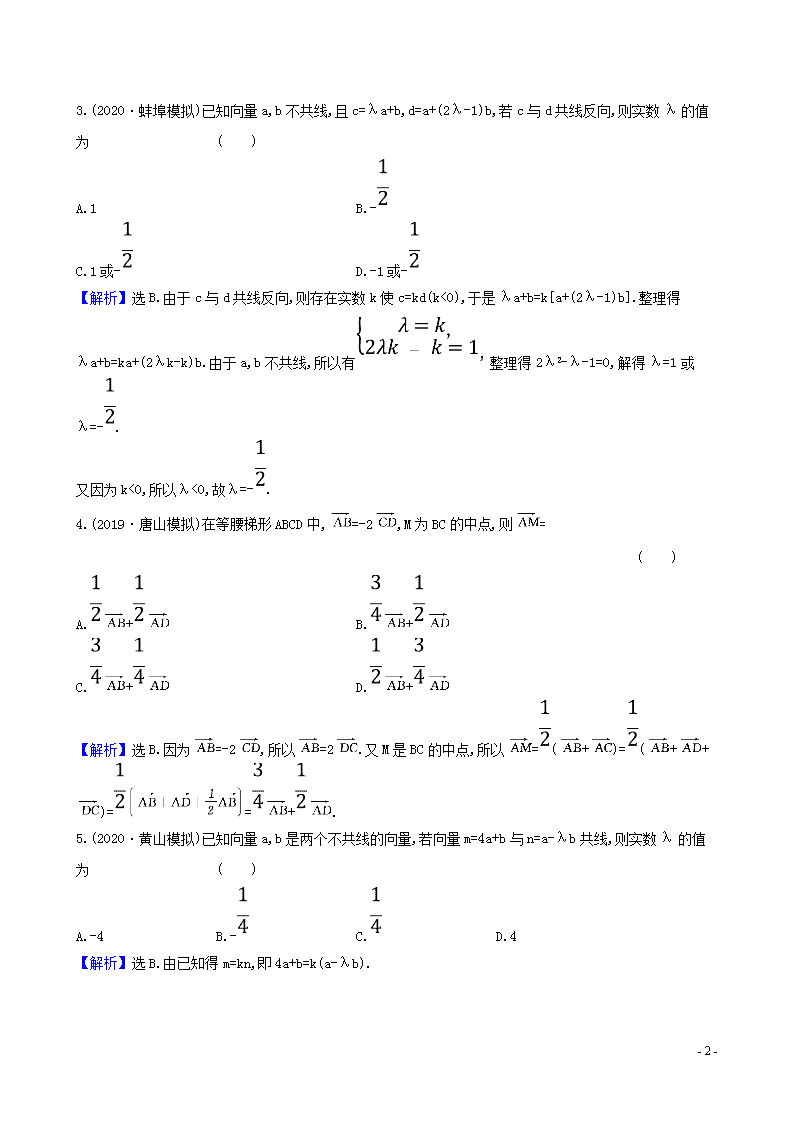2021版高考数学一轮复习核心素养测评二十七平面向量的概念及其线性运算理北师大版 7页

核心素养测评二十七 平面向量的概念及其线性运算 ‎(25分钟　50分)‎ 一、选择题(每小题5分,共35分)‎ ‎1.下列说法正确的是 (　　)‎ A.方向相同或相反的向量是平行向量 B.零向量是0‎ C.长度相等的向量叫做相等向量 D.共线向量是在一条直线上的向量 ‎【解析】选B.对于选项A,因为方向相同或相反的非零向量是平行向量,所以该说法错误;对于选项B,因为零向量就是0,所以该说法正确;对于选项C,方向相同且长度相等的向量叫相等向量,所以该说法错误;对于选项D,共线向量所在直线可能重合,也可能平行,所以该说法错误.‎ ‎2.在△ABC中,D,E,F分别是AB,BC,AC的中点,则= (　　)‎ A.+　　　　　 B.+‎ C.+　 D.+‎ ‎【解析】选D.如图,因为=,又因为=+,所以=+.‎ ‎【变式备选】‎ 如图,向量a-b等于 (　　)‎ A.-4e1-2e2　　　　　 B.-2e1-4e2‎ C.e1-3e2 D.3e1-e2‎ ‎【解析】选C.由题图可知a-b=e1-3e2.‎ - 7 -‎ ‎3.(2020·蚌埠模拟)已知向量a,b不共线,且c=λa+b,d=a+(2λ-1)b,若c与d共线反向,则实数λ的值为 (　　)‎ A.1　 B.-‎ C.1或-　 D.-1或-‎ ‎【解析】选B.由于c与d共线反向,则存在实数k使c=kd(k<0),于是λa+b=k[a+(2λ-1)b].整理得λa+b=ka+(2λk-k)b.由于a,b不共线,所以有整理得2λ2-λ-1=0,解得λ=1或λ=-.‎ 又因为k<0,所以λ<0,故λ=-.‎ ‎4.(2019·唐山模拟)在等腰梯形ABCD中,=-2,M为BC的中点,则=‎ ‎(　　)‎ A.+ B.+‎ C.+ D.+‎ ‎【解析】选B.因为=-2,所以=2.又M是BC的中点,所以=(+)=(++)==+.‎ ‎5.(2020·黄山模拟)已知向量a,b是两个不共线的向量,若向量m=4a+b与n=a-λb共线,则实数λ的值为 (　　)‎ A.-4　　 B.- C. D.4‎ ‎【解析】选B.由已知得m=kn,即4a+b=k(a-λb).‎ - 7 -‎ 所以解得 ‎6.矩形ABCD的对角线相交于点O,E为AO的中点,若=λ+μ(λ,μ为实数),则λ2+μ2= (　　)‎ A. B. C.1 D.‎ ‎【解析】选A.=+=+=+(+)=-,‎ 所以λ=,μ=-,‎ 所以λ2+μ2=.‎ ‎7.(2020·长治模拟)设向量a,b不共线,=2a+pb,=a+b,=a-2b,若A,B,D三点共线,则实数p的值为 (　　)‎ A.-2　 B.-1　 C.1　 D.2‎ ‎【解析】选B.因为=a+b,=a-2b,‎ 所以=+=2a-b.‎ 又因为A,B,D三点共线,所以,共线.‎ 设=λ,所以2a+pb=λ(2a-b),‎ 所以2=2λ,p=-λ,即λ=1,p=-1.‎ 二、填空题(每小题5分,共15分)‎ ‎8.在如图所示的方格纸中,向量a,b,c的起点和终点均在格点(小正方形顶点)上,若c与xa+yb(x,y为非零实数)共线,则的值为________________. ‎ - 7 -‎ ‎【解析】设e1,e2分别为水平方向(向右)与竖直方向(向上)的单位向量,则向量c=e1-2e2,a=2e1+e2,b=-2e1-2e2,由c与xa+yb共线,得c=λ(xa+yb),所以e1-2e2=2λ(x-y)e1+λ(x-2y)e2,‎ 所以所以则的值为.‎ 答案:‎ ‎9.(2020·侯马模拟)设向量a,b不平行,向量λa+b与a+2b平行,则实数λ=________________. ‎ ‎【解析】因为向量λa+b与a+2b平行,‎ 所以可设λa+b=k(a+2b),则所以λ=.‎ 答案:‎ ‎10.直线l上有不同的三点A,B,C,O是直线l外一点,对于向量=(1-cos α)+ sin α(α是锐角)总成立,则α=________________.  ‎ ‎【解析】因为直线l上有不同的三点A,B,C,所以存在实数λ,使得=λ,‎ 所以-=λ(-),‎ 即=+λ,‎ 所以所以sin α=cos α,‎ 因为α是锐角,所以α=45°.‎ 答案:45°‎ ‎(15分钟　35分)‎ - 7 -‎ ‎1.(5分)(2020·晋城模拟)在平面直角坐标系中,O为坐标原点,A,B,C三点满足=+,则等于 (　　)‎ A.1　 B.2　 C.3　　 D.‎ ‎【解析】选C.因为=-=+-=,=-= +-=,‎ 所以=3. ‎ ‎2.(5分)(2020·朔州模拟)在△ABC中,+=2,+=0,若=x+y,则 (　　)‎ A.y=3x B.x=3y C.y=-3x D.x=-3y ‎【解析】选D.因为+=2,所以点D是BC的中点,又因为+=0,所以点E是AD的中点,所以有:=+=-+=-+×(+)=-+,因此x=-,y=⇒x=-3y.‎ ‎3.(5分)(2020·合肥模拟)设D,E,F分别为△ABC三边BC,CA,AB的中点,则+2+3= (　　)‎ A.　　　　　　 B.‎ C. D.‎ ‎【解析】选D.因为D,E,F分别为△ABC三边BC,CA,AB的中点,所以+2+3=(+)+2×(+)+3××(+)‎ ‎=+++++=++=+=.‎ ‎4.(10分)如图,在△ABC中,D为BC的四等分点,且靠近B点,E,F分别为AC,AD的三等分点,且分别靠近A,D两点,设=a,=b. ‎ - 7 -‎ ‎(1)试用a,b表示,,.‎ ‎(2)证明:B,E,F三点共线.‎ ‎【解析】(1)在△ABC中,因为=a,=b,‎ 所以=-=b-a,=+=+ =a+(b-a)=a+ b,=+=-+=-a+b.‎ ‎(2)因为=-a+b,=+=-+=-a+=-a+b=(-a+b),所以=,与共线,且有公共点B,所以B,E,F三点共线.‎ ‎5.(10分)经过△OAB的重心G的直线与OA,OB分别交于点P,Q,设=m,=n,m,n∈R+,求m+n的最小值. ‎ ‎【解析】设=a,=b,由题意知 ‎=×(+)=(a+b),‎ ‎=-=nb-ma,‎ ‎=-=a+b,‎ 由P,G,Q三点共线得,存在实数λ,使得=λ,即nb-ma=λa+λb,‎ - 7 -‎ 从而消去λ得+=3.‎ 于是m+n=(m+n)‎ ‎=≥(2+2)=.‎ 当且仅当m=n=时,m+n取得最小值.‎ - 7 -‎