高中数学选修2-1课件2_2_2双曲线的简单几何性质(2) 24页

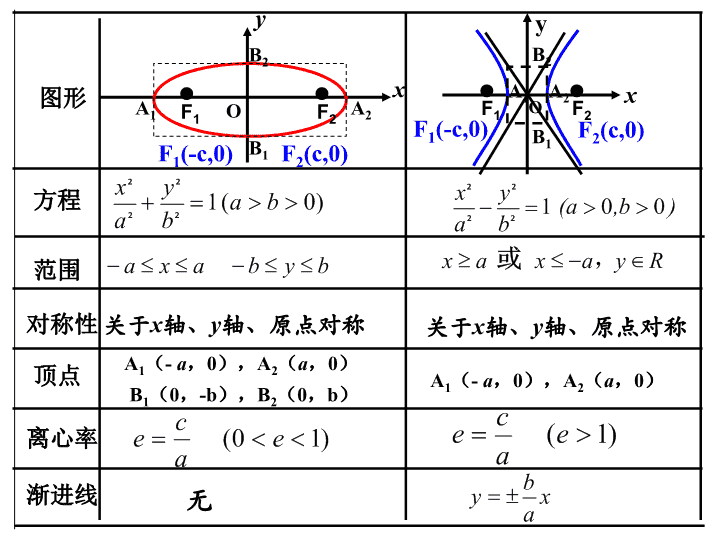
2.3.2 双曲线的几何性质 ( 二 ) 没有学不会的课程， 没有考不高的分数 数载心血，用心打造 高效课堂的完美品质！ 关于 x 轴、 y 轴、原点对称 图形 方程 范围 对称性 顶点 离心率 y x O A 2 B 2 A 1 B 1 . . F 1 F 2 y B 2 A 1 A 2 B 1 x O . . F 2 F 1 A 1 （ - a ， 0 ）， A 2 （ a ， 0 ） B 1 （ 0 ， -b ）， B 2 （ 0 ， b ） F 1 (-c,0) F 2 (c,0) F 1 (-c,0) F 2 (c,0) 关于 x 轴、 y 轴、原点对称 A 1 （ - a ， 0 ）， A 2 （ a ， 0 ） 渐进线 无 关于 x 轴、 y 轴、原点对称 图形 方程 范围 对称性 顶点 离心率 A 1 （ - a ， 0 ）， A 2 （ a ， 0 ） A 1 （ 0 ， - a ）， A 2 （ 0 ， a ） 关于 x 轴、 y 轴、原点对称 渐进线 . . y B 2 A 1 A 2 B 1 x O F 2 F 1 x B 1 y O . F 2 F 1 B 2 A 1 A 2 . F 1 (-c,0) F 2 (c,0) F 2 (0,c) F 1 (0,-c) 1 、“共渐近线”的双曲线 λ>0 表示焦点在 x 轴上的双曲线； λ<0 表示焦点在 y 轴上的双曲线。 2 、“共焦点”的双曲线 （ 1 ）与椭圆 有共同焦点的双曲线方程表 示为 （ 2 ）与双曲线 有共同焦点的双曲线方 程表示为 复习练习： C B 例 1 、双曲线型自然通风塔的外形，是双曲线 　　的一部分绕其虚轴旋转所成的曲面，它的 　　最小半径为 12m, 上口半径为 13m, 下口半径 　　为 25m, 高 55m. 选择适当的坐标系，求出此 　　双曲线的方程 ( 精确到 1m). A′ A 0 x C′ C B′ B y 13 12 25 例题讲解 --- 实际应用题 同步导学 45 页 解：如图，建立直角坐标系 xOy, 使小圆的直径 AA‘ 在 x 轴上，圆心与原点重合。这时，上下口的直径 CC’,BB’ 都平行于 x 轴，且 ︱CC’ ︱=13×2, ︱BB’ ︱ ＝ 25×2 C x y O A’ A C’ B B’ 13 12 25 用计算器解方程，得 b≈25 C x y O A’ A C’ B B’ 13 12 25 例题讲解 ---- 直线与双曲线问题： 例 2 ：如图所示，过双曲线 的右焦点 F 2 ,倾斜角为 30 °的直线交双曲线于A，B两点，求|AB| F 1 F 2 x y O A B 法一 : 设直线 AB 的方程为 与双曲线方程联立得 A 、 B 的坐标为 由两点间的距离公式得 |AB|= 例 2 ：如图所示，过双曲线 的右焦点 F 2 ,倾斜角为 30 °的直线交双曲线于A，B两点，求|AB| F 1 F 2 x y O A B 法二 : 设直线 AB 的方程为 与双曲线方程联立消 y 得 5x 2 +6x-27=0 由两点间的距离公式得 设 A 、 B 的坐标为 (x 1 ,y 1 ) 、 (x 2 ,y 2 ), 则 你能求出△ AF 1 B 的周长吗 ? 例题讲解 --- 焦点三角形 例 3 、由双曲线 上的一点 P 与左、右 两焦点 构成 ，求 的内切圆与 边 的切点坐标。 说明： 双曲线上一点 P 与双曲线的两个焦点 构成的三角形称之为 焦点三角形 ，其中 和 为三角形的三边。解决与这个三角形有关的问题，要充分利用双曲线的定义和三角形的边角关系、正弦定理、余弦定理。 点 P 与定点 F(5 ， 0) 的距离和它到定直线 的距离之比为 5:4, 求点 P 的轨迹方程。 【例 4 】 点 P 与定点 F(0 ， 7) 的距离和它到定直线 的距离之比为 7:4, 求点 P 的轨迹方程。 例题讲解 --- 第二定义及焦半径 平面内与一个 定点 的距离和到 定直线 的距离的比 是 常数 e= (e>1) 的动点的轨迹是双曲线。 焦点 F 1 (c,0) 对应的 准线方程为 焦点 F 2 (-c,0) 对应的 准线方程为 应用 1 ： 双曲线 右支上有一点 P ，它到右焦点的 距离为 8 ，求： (1) 点 P 到右准线的距离； (2) 点 P 到双曲线左准线的距离。 在双曲线 上求一点 M ，使 M 到左焦点 的距离是它到右焦点距离的两倍。 应用 2 ： 应用 3 ：参考同步导学 46 页例 3 已知点 A(3,2), F(2,0), 在双曲线 上求一点 P ，使得 |PA|+1/2|PF| 最小 , 并求最小距离。 已知双曲线 的两个焦点分别 为 F 1 (-c,0),F 2 (c,0),P(x 0 ,y 0 ) 是双曲线上任一点， 证明： |PF 1 |=|ex 0 +a | ,|PF 2 |= | ex 0 - a | 应用 4 ：