专题8-7+立体几何中的向量方法（测）-2018年高考数学一轮复习讲练测（浙江版） 22页

‎2018年高考数学讲练测【浙江版】【测】第八章 立体几何 第07节 立体几何中的向量方法 班级__________ 姓名_____________ 学号___________ 得分__________‎ 一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的.）‎ ‎1. 已知平面的法向量为，点不在内，则直线与平面的位置关系为 A． B． C．与相交不垂直 D． ‎【答案】D ‎【解析】，而点不在内，故 ‎2.【浙江省杭州市萧山区第一中学月考】若a‎=(2,-1,0)‎，b‎=(3,-4,7)‎，且‎（λa+b)⊥‎a，则λ的值是（ ）‎ A. 0 B. 1 C. -2 D. 2‎ ‎【答案】C ‎3.【2017年河南省信阳市期末】设a‎=(3,-2,-1)‎是直线的方向向量，n‎=(1,2,-1)‎是平面a的法向量，则（ ）‎ A. l⊥a B. l∥a C. l⊂a或l⊥a D. l∥a或l⊂a ‎【答案】D ‎【解析】‎ 因为a‎∙n=3×1+‎-2‎×2+‎-1‎×‎-1‎=0‎，所以a‎⊥‎n，即l∥a或l⊂a.故选D.‎ ‎4.【2017年福建省数学基地校】二面角的棱上有、两点，直线、分别在这个二面角的两个半平面内，且都垂直于.已知， ， ， ，则该二面角的大小为(　　)‎ ‎(A) 　 (B) 　 (C) 　　 (D) ‎【答案】C ‎【解析】由条件知， ， .‎ ‎∴ .‎ ‎∴， ，∴二面角的大小为；‎ 故选C.‎ ‎5. 如图，正方形ABCD与矩形ACEF所在平面互相垂直，AB＝，AF＝1，M在EF上，且AM∥平面BDE.则M点的坐标为 (　　)‎ A．(1，1，1) 　　 B. C. 　　 D. 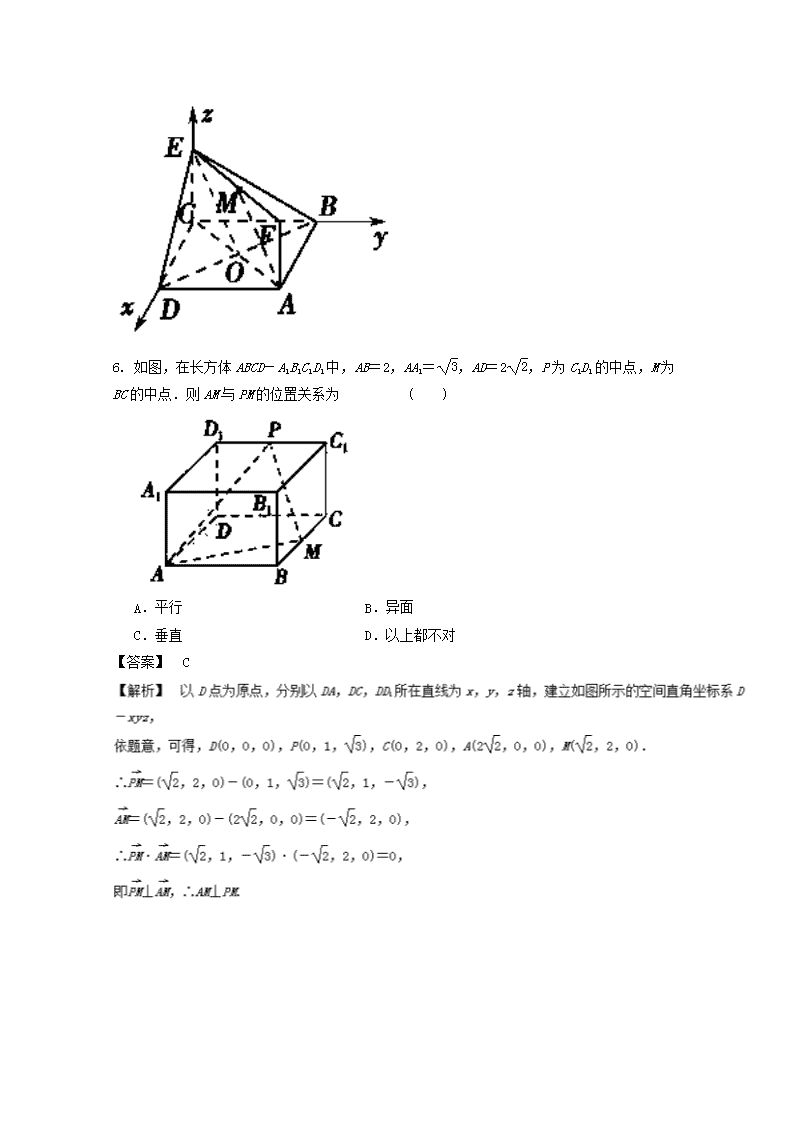‎【答案】　C ‎6. 如图，在长方体ABCD－A1B1C1D1中，AB＝2，AA1＝，AD＝2，P为C1D1的中点，M为BC的中点．则AM与PM的位置关系为 (　　)‎ A．平行 B．异面 C．垂直 D．以上都不对 ‎【答案】　C ‎7. 已知A(1,0,0)，B(0,1,0)，C(0,0,1)，则平面ABC的一个单位法向量是(　　)‎ A. B. C. D. ‎【答案】D ‎【解析】因为A(1,0,0)，B(0,1,0)，C(0,0,1)，‎ 所以＝(－1,1,0)，＝(－1,0,1)．‎ 经验证，当n＝时，‎ n·＝－＋0＝0，n·＝＋0－＝0，故选D.‎ ‎8. 如图，正方体ABCD—A1B‎1C1D1中，E，F分别在A1D，AC上，且A1E＝A1D，AF＝AC，则(　　)‎ A．EF至多与A1D，AC之一垂直 B．EF⊥A1D，EF⊥AC C．EF与BD1相交 D．EF与BD1异面 ‎【答案】B ‎9. 已知长方体，下列向量的数量积一定不为的是 （ ）‎ B A C D A1‎ B1‎ C1‎ D1‎ A． B． C． D． ‎【答案】D ‎【解析】当侧面是正方形时可得=0，所以排除A.当底面ABCD是正方形时AC垂直于对角面.所以排除B.显然排除C.由图可得与BC所成的角小于.故选D.‎ ‎10. 已知空间四边形ABCD的每条边和对角线的长都等于a，点E，F分别是BC，AD的中点，则·的值为 (　　)‎ A．a2 B.a‎2 ‎ C.a2 D.a2‎ ‎【答案】　C ‎11．【2017学山东省烟台市期末】在三棱柱ABC-‎A‎1‎B‎1‎C‎1‎中，底面为正三角形，侧棱垂直底面，AB=4,AA‎1‎=6‎.若E,F分别是棱BB‎1‎,CC‎1‎上的点，且BE=B‎1‎E,C‎1‎F=‎1‎‎3‎CC‎1‎，则异面直线A‎1‎E与AF所成角的余弦值为（ ）‎ A. ‎-‎‎2‎‎6‎ B. ‎2‎‎6‎ C. ‎-‎‎2‎‎10‎ D. ‎‎2‎‎10‎ ‎【答案】D ‎【解析】‎ 以C 为原点,CA 为x 轴,在平面ABC 中过作AC 的垂线为y 轴,CC‎1‎为z 轴,建立空间直角坐标系, ‎∵‎ 在三棱柱ABC-‎A‎1‎B‎1‎C‎1‎ 中,底面为正三角形,侧棱垂直底面,AB=4,AA‎1‎=6‎, E,F分别是棱BB‎1‎,CC‎1‎上的点,且BE=B‎1‎E,C‎1‎F=‎1‎‎3‎CC‎1‎, ‎∴A‎1‎(4,0,6),E(2,2‎3‎,3),F(0,0,4),A(4,0,0)‎ ‎ A‎1‎E‎=(-2,3‎3‎,-3),AF=(-4,0,4)‎‎ , 设异面直线A‎1‎E与AF所成角所成角为θ , 则cosθ=‎|A‎1‎E⋅AF||‎‎|A‎1‎E|⋅‎|AF||‎=‎4‎‎20‎‎2‎=‎‎2‎‎10‎ .所以异面直线A‎1‎E与AF所成角的余弦值为‎2‎‎10‎ .故选D.‎ ‎12.【甘肃西北师大附中高三11月月考】已知等差数列的前n项和为，且，则过点和的直线的一个方向向量的坐标可以是（ ）‎ A． B．(2，4) C． D.（-1，-1）‎ ‎【答案】A 二、填空题（本大题共4小题，每小题5分，共20分。把答案填在题中的横线上。）‎ ‎13．【2018届河北省定州中学高三上第二次月考】已知点P在正方体ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎的对角线BD‎1‎上，H在B‎1‎D‎1‎上，则DP与CC‎1‎所成角的大小为___________.‎ ‎【答案】‎‎45‎‎∘‎ ‎14．在三棱柱中，侧棱底面， ， ， ，若直线与直线的夹角的余弦值是，则棱的长度是__________．‎ ‎【答案】 ‎ ‎【解析】‎ 如图建立坐标系设 ，则 ‎15．【2017届河北省衡水中学押题卷】如图所示，在棱长为2的正方体中， ， 分别是， 的中点，那么异面直线和所成角的余弦值等于__________．‎ ‎【答案】 ‎16.【2018届浙江省名校协作体高三上学期考试】如图，棱长为的正方体的顶点在平面内，三条棱, , 都在平面的同侧. 若顶点, 到平面的距离分别为,，则平面与平面所成锐二面角的余弦值为________‎ ‎【答案】 ‎【解析】建立如图所示的空间直角坐标系，设平面 的一个法向量为 ，设 ‎ 令 可得 设， ‎ 解得 ； 则的法向量为 由 得， ‎ ‎∴，平面 的法向量为，则平面与平面所成锐二面角的余弦值为 ‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.（本小题满分10分）【2018届贵州省黔东南州高三上第一次联考】如图所示，在四棱锥中，四边形为菱形， 为正三角形，且分别为的中点， 平面， 平面．‎ ‎（1）求证： 平面；‎ ‎（2）求与平面所成角的正弦值．‎ ‎【答案】（1）见解析；（2）.‎ 试题解析：‎ ‎（1）证明：因为平面， 平面，‎ 所以，‎ 又平面平面，所以平面，‎ 由四边形菱形，得，‎ 所以平面．‎ ‎（2）解：‎ 以为原点， 分别为轴建立空间直角坐标系，‎ 不妨设菱形的边长为2，则，‎ ‎，‎ 则点，‎ ‎，‎ 设平面的法向量为，‎ 则由，解得，‎ 不妨令，得；‎ 又，‎ 所以与平面所成角的正弦值为．‎ ‎18．（本小题满分12分）【2018届湖北省部分重点中学高三起点】在如图所示的多面体中，四边形为正方形，底面为直 角梯形， 为直角， ∥， ，平面平面.‎ ‎（Ⅰ）求证： ；‎ ‎（Ⅱ）若，求二面角的余弦值.‎ ‎【答案】(Ⅰ)证明见解析；(Ⅱ) .‎ 设，以所在直线分别为轴建立如图坐标系，‎ 则， ， ， ， ， ，‎ ‎∵，∴.‎ ‎（2）由（1）知是平面的一个法向量，设是平面的法向量，‎ ‎∵，∴， ，∴， ，由，得，由，得，令，得，故是平面的一个法向量，∴，即二面角的余弦值为.‎ ‎19. （本小题满分12分）【2017课标3，理19】如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．‎ ‎（1）证明：平面ACD⊥平面ABC；‎ ‎（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.‎ ‎【答案】(1)证明略；‎ ‎(2) .‎ ‎【解析】‎ ‎（2）‎ 由题设及（1）知，两两垂直，以为坐标原点，的方向为轴正方向，为单位长，建立如图所示的空间直角坐标系.则 ‎ 由题设知，四面体ABCE的体积为四面体ABCD的体积的，从而E到平面ABC的距离为D到平面ABC的距离的，即E为DB的中点，得 .故 ‎ ‎20. （本小题满分12分）如图，四棱锥P﹣ABCD的底面是边长为1的正方形，PA⊥底面ABCD，E、F分别为AB、PC的中点．‎ ‎（Ⅰ）求证：EF∥平面PAD；‎ ‎（Ⅱ）若PA=2，试问在线段EF上是否存在点Q，使得二面角Q﹣AP﹣D的余弦值为？若存在，确定点Q的位置；若不存在，请说明理由．‎ ‎【答案】（Ⅰ）见解析；（Ⅱ）满足条件的Q存在，是EF中点．‎ ‎（Ⅱ）结论：满足条件的Q存在，是EF中点．理由如下：如图：以点A为坐标原点建立空间直角坐标系，‎ 则P（0，0，2），B（0，1，0），C（1，1，0），E（0，，0），F（，，1），‎ 由题易知平面PAD的法向量为=（0，1，0），假设存在Q满足条件：设，‎ ‎∵，∴，，λ∈[0，1]，‎ 设平面PAQ的法向量为，由，可得，‎ ‎∴，由已知：，解得：，‎ 所以满足条件的Q存在，是EF中点．‎ ‎21.（本小题满分12分）【2016高考天津理数】如图，正方形ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.‎ ‎（I）求证：EG∥平面ADF；‎ ‎（II）求二面角O-EF-C的正弦值；‎ ‎（III）设H为线段AF上的点，且AH=HF，求直线BH和平面CEF所成角的正弦值.‎ ‎【答案】（Ⅰ）详见解析（Ⅱ）（Ⅲ） .‎ ‎（I）证明：依题意，.设为平面的法向量，则，即 .不妨设，可得，又，可得，又因为直线，所以.‎ ‎（II）解：易证，为平面的一个法向量.依题意，.设为平面的法向量，则，即 .不妨设，可得.‎ 因此有，于是，所以，二面角 的正弦值为.‎ ‎（III）解：由，得.因为，所以，进而有，从而，因此.所以，直线和平面所成角的正弦值为.‎ ‎22. （本小题12分）【2016年高考北京理数】如图，在四棱锥中，平面平面，，，，，，.‎ ‎（1）求证：平面；‎ ‎（2）求直线与平面所成角的正弦值；‎ ‎（3）在棱上是否存在点，使得平面？若存在，求的值；若不存在，说明理由.‎ ‎【答案】（1）见解析；（2）；（3）存在， 试题解析：（1）因为平面平面，，‎ 所以平面，所以，‎ 又因为，所以平面；‎ ‎（2）取的中点，连结，，‎ 因为，所以.‎ 又因为平面，平面平面，‎ 所以平面.‎ 因为平面，所以.‎ 因为，所以.‎ 如图建立空间直角坐标系，由题意得，‎ .‎ 设平面的法向量为，则 即 令，则.‎ 所以.‎ 又，所以.‎ 所以直线与平面所成角的正弦值为.‎ ‎（3）设是棱上一点，则存在使得.‎ 因此点.‎ 因为平面，所以平面当且仅当，‎ 即，解得.‎ 所以在棱上存在点使得平面，此时.‎ ‎ ‎