山东省济宁市第二中学2019-2020学年高一上学期期中考试数学试卷 (1) 8页

www.ks5u.com ‎ 数 学 试 题 2019.11 ‎ 本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共4页.满分150分，考试时间120分钟.‎ 注意事项：‎ ‎1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.‎ ‎2．第I卷（选择题）选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试卷上.‎ ‎3. 第II卷（非选择题）请用0.5毫米黑色签字笔在相应位置处答题，如需改动，用“”划掉重新答题.‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. ‎ ‎1．设集合，，，则 ‎ A． B． C． D．‎ ‎2. 若命题，则命题的否定是 ‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎3. 若，则下列不等式中正确的是 ‎ ‎ A. B. C. D. ‎ ‎4．下列函数中，既是偶函数又在区间上单调递减的是 ‎ A． B． C． D．‎ ‎5. 若关于的不等式的解集为，则实数的值是 ‎ ‎ A． B．‎ ‎ C． D．‎ ‎6．三个数之间的大小关系是 ‎ A． B． C． D．‎ ‎7．要制作一个容积为4，高为1的无盖长方体容器.‎ 已知该容器的底面造价是每平方米30元，‎ ‎ 侧面造价是每平方米10元，则该容器的最低总造价是 ‎ ‎ A. 120元 B．160元 C．200元 D．240元 ‎8．已知，则“”是“”的 ‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎9. 函数的单调递增区间是 ‎ A. 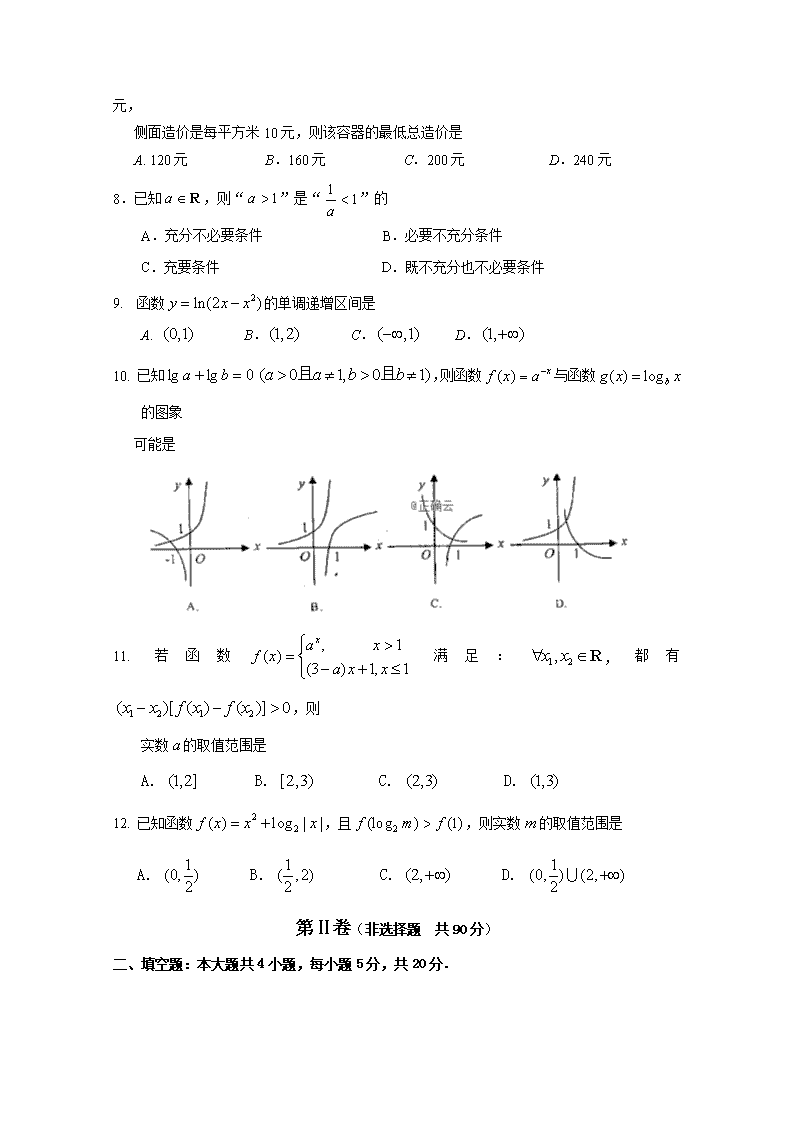B． C． D．‎ ‎10. 已知，则函数与函数的图象 ‎ 可能是 ‎ ‎11. 若函数 满足：，都有，则 ‎ 实数的取值范围是 ‎ ‎ A． B． C. D. ‎ ‎12. 已知函数，且，则实数的取值范围是 ‎ ‎ A． B． C. D. ‎ ‎2,4,6‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13. 已知函数, 则= ▲ . ‎ ‎14．函数的定义域为 ▲ . ‎ ‎15. 已知函数，若，则 ▲ . ‎ ‎16. 已知正数满足，则的最小值为 ▲ . ‎ 三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.‎ ‎17. （本小题满分10分）‎ ‎ 已知，，求的值.‎ ‎18. （本小题满分12分）‎ 已知函数为奇函数.‎ ‎ （Ⅰ）判断并证明函数的奇偶性；‎ ‎ （Ⅱ）若时，. 当时，求函数的解析式.‎ ‎19.（本小题满分12分）‎ ‎ 已知函数 ‎（Ⅰ）画出函数的图象，并写出其单调递减区间(不需证明)；‎ ‎ （Ⅱ）若关于的方程有4个不同的实数解，求实 ‎ ‎ 数的取值范围.‎ ‎20.（本小题满分12分）‎ ‎ 已知全集，集合.‎ ‎（Ⅰ）若，求集合；‎ ‎ （Ⅱ）若，求实数的取值范围.‎ ‎21.（本小题满分12分）‎ ‎ 小李大学毕业后选择自主创业，开发了一种新型电子产品.2019年9月1日投入市场销售，在9月份的30天内，前20天每件售价（元）与时间（天，‎ ‎）满足一次函数关系，其中第一天每件售价为63元，第10天每件售价为90元；后10天每件售价均为120元.已知日销售量（件）与时间（天）之间的函数关系是.‎ ‎ （Ⅰ）写出该电子产品9月份每件售价（元）与时间（天）的函数关系式；‎ ‎ （Ⅱ）9月份哪一天的日销售金额最大？并求出最大日销售金额. ‎ ‎ (日销售金额=每件售价日销售量).‎ ‎22.（本小题满分12分）‎ ‎ 已知函数.‎ ‎（Ⅰ）判断并证明的单调性； ‎ ‎（Ⅱ）是否存在实数，使函数为奇函数？证明你的结论；‎ ‎（Ⅲ）在（Ⅱ）的条件下，当时，恒成立，求实数的取值范围.‎ ‎ 数学试题 参考答案 2019.11‎ 一、选择题（5分12=60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C D D A C C A A B B D 二、填空题（5分4=20分）‎ ‎13. 14. 15. 16. ‎ 三、解答题 ‎17．解：原式=……………………………5分 将的值代入上式得 原式……10分 ‎18. 解：（Ⅰ）由得. ……………………1分 又为奇函数，‎ ‎，…………………4分 为奇函数. ……………………………………………………6分 ‎（Ⅱ）当时，，‎ 当时，， ……………9分 又为奇函数， ‎ 所以当时，. ………………………………12分 ‎19.解：（Ⅰ）该函数的图象如图所示： ‎ ‎ …………………………………………4分 其单调递减区间为………………………………………………6分 ‎（Ⅱ）由图象可知 …………………………………………9分 即 ‎ ‎ 故实数的取值范围是……………………………………12分 ‎20．解：（Ⅰ），……………………………………………1分 ‎ ‎………………………………………………………………2分 若，则………………………3分 ‎…………………………………………………4分 ‎（Ⅱ）,，………………………………………………6分 ‎，方程的根为 ①当时， ， ………………8分 ②当时， ，符合， ……………………………9分 ③当时， ，符合， ………………11分 综上，实数的取值范围是.……………………………………………12分 ‎21. 解：（Ⅰ）设前20天每件售价（元）与时间（天）的函数关系式为.‎ 由题意得 ………………………………………………………2分 解得 …………………………………………………………3分 故该电子产品9月份每件售价（元）与时间（天）的函数关系式为 ‎…………………………………………………5分 ‎（Ⅱ）设9月份日销售金额为元，则有 ‎……………………………………7分 ①当时，的对称轴为.‎ 在上为增函数，在上为减函数.‎ 当时，………………………………………………………9分 ②当时，为减函数.‎ 当时，……………………………………………………11分 综上所述，9月份第10天的日销售金额最大，最大为3675元.………………12分 ‎22.解：（Ⅰ）任取，且，则 ‎……2分 ‎，即 又，‎ ‎，即………………………………………………3分 在上为增函数…………………………………………………………………4分 ‎（Ⅱ）假设存在实数，使函数为奇函数,‎ ‎,，即. ………………………………………6分 ‎ ‎ 时,是上的奇函数. …………………………………………………8分 ‎（Ⅲ）即恒成立，‎ ‎∵，∴，即 ‎∴（）恒成立，………………………………………………9分 设（），则……………10分 当且仅当，即时等号成立. ‎ 的最小值为 ……………………………………………………11分 ‎∴‎ 即实数的取值范围为.……………………………………………12分