2019年高考数学高分突破复习课件考前冲刺三 第四类 12页

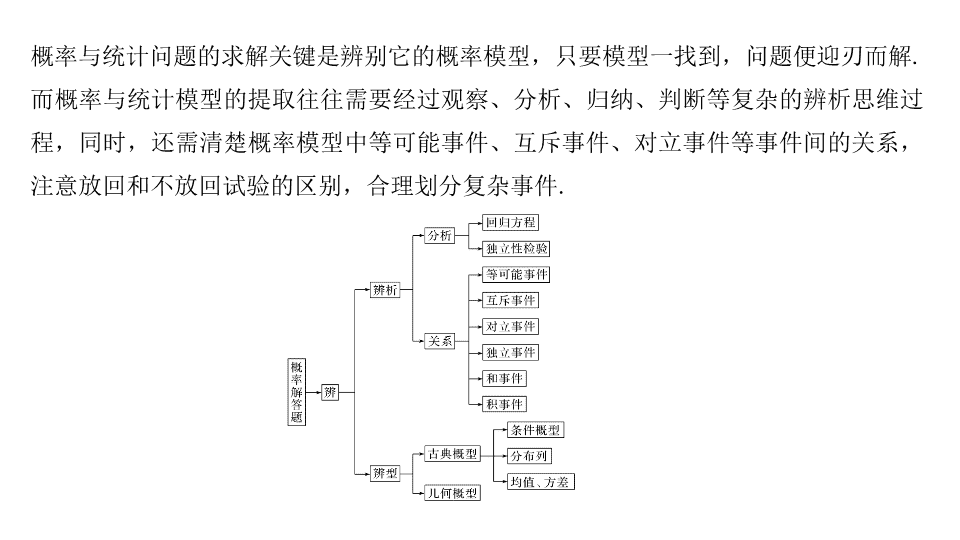
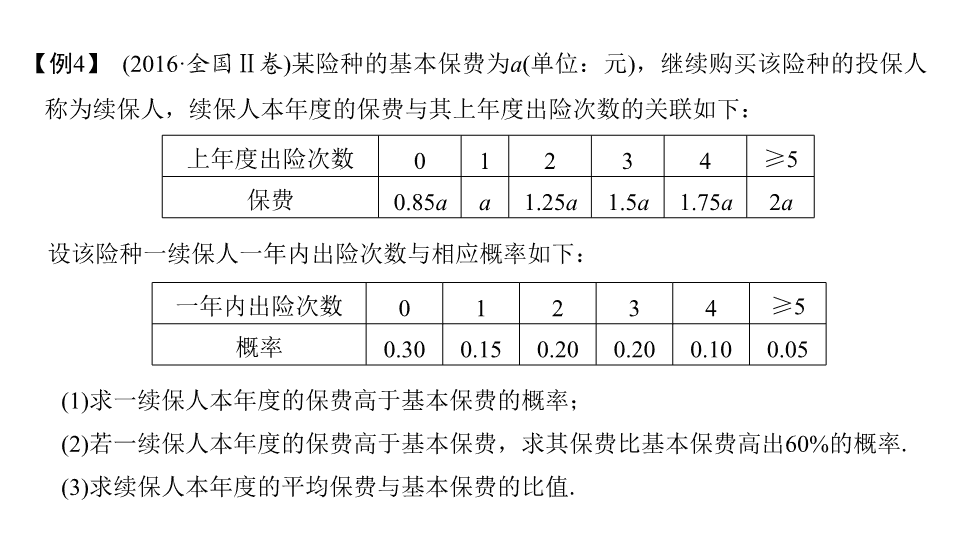
第四类　概率问题重在 “ 辨 ” —— 辨析、辨型 概率与统计问题的求解关键是辨别它的概率模型，只要模型一找到，问题便迎刃而解 . 而概率与统计模型的提取往往需要经过观察、分析、归纳、判断等复杂的辨析思维过程，同时，还需清楚概率模型中等可能事件、互斥事件、对立事件等事件间的关系，注意放回和不放回试验的区别，合理划分复杂事件 . 【例 4 】 (2016· 全国 Ⅱ 卷 ) 某险种的基本保费为 a ( 单位：元 ) ，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下： 设该险种一续保人一年内出险次数与相应概率如下： (1) 求一续保人本年度的保费高于基本保费的概率； (2) 若一续保人本年度的保费高于基本保费，求其保费比基本保费高出 60% 的概率 . (3) 求续保人本年度的平均保费与基本保费的比值 . 上年度出险次数 0 1 2 3 4 ≥ 5 保费 0.85 a a 1.25 a 1.5 a 1.75 a 2 a 一年内出险次数 0 1 2 3 4 ≥ 5 概率 0.30 0.15 0.20 0.20 0.10 0.05 解 　 (1) 设 A 表示事件： “ 一续保人本年度的保费高于基本保费 ” ，则事件 A 发生当且仅当一年内出险次数大于 1 ， ( 辨析 1) 故 P ( A ) ＝ 0.20 ＋ 0.20 ＋ 0.10 ＋ 0.05 ＝ 0.55. ( 辨型 1) (2) 设 B 表示事件： “ 一续保人本年度的保费比基本保费高出 60% ” ，则事件 B 发生当且仅当一年内出险次数大于 3 ， ( 辨析 2) 故 P ( B ) ＝ 0.10 ＋ 0.05 ＝ 0.15. 又 P ( AB ) ＝ P ( B ) ， (3) 记续保人本年度的保费为 X ，则 X 的分布列为 E ( X ) ＝ 0.85 a × 0.30 ＋ a × 0.15 ＋ 1.25 a × 0.20 ＋ 1.5 a × 0.20 ＋ 1.75 a × 0.10 ＋ 2 a × 0.05 ＝ 1.23 a . 因此续保人本年度的平均保费与基本保费的比值为 1.23. X 0.85 a a 1.25 a 1.5 a 1.75 a 2 a P 0.30 0.15 0.20 0.20 0.10 0.05 ( 辨型 3) 探究提高 　 1. 辨析 (1) ：判断事件 A 发生，在一年内出险次数为 2 ， 3 ， 4 或 ≥ 5. 辨型 (1) ：该问题为求随机事件的概率，利用互斥事件的概率加法公式求解 . 辨析 (2) ：判断事件 B 发生，在一年内出险次数为 4 或 ≥ 5. 辨型 (2) ：该问题为条件概率，可利用公式求解 . 2 . 求解此类问题的关键： (1) 会判断，先判断事件的类型，再利用对立事件的概率公式、条件概率的公式等求解概率； (2) 会计算，要求随机变量 X 的期望，需先求出 X 的所有可能取值，然后求出随机变量 X 取每个值时的概率，再利用随机变量的数学期望的定义进行计算 . 【训练 4 】 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务，由于其依托 “ 互联网＋ ” ，符合 “ 低碳出行 ” 的理念，已越来越多地引起了人们的关注 . 某部门为了对该城市共享单车加强监管，随机选取了 50 人就该城市共享单车的推行情况进行问卷调查，并将问卷中的这 50 人根据其满意度评分值 ( 百分制 ) 按照 [50 ， 60) ， [60 ， 70) ， … ， [90 ， 100] 分成 5 组，请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图 ( 如图所示 ) 的解决下列问题： 频率分布表 组别 分组 频数 频率 第 1 组 [50 ， 60) 8 0.16 第 2 组 [60 ， 70) a ■ 第 3 组 [70 ， 80) 20 0.40 第 4 组 [80 ， 90) ■ 0.08 第 5 组 [90 ， 100] 2 b   合计 ■ ■ 频率分布直方图 (1) 求出 a ， b ， x 的值； (2) 若在满意度评分值为 [80 ， 100] 的人中随机抽取 2 人进行座谈，设所抽取的 2 人中来自第 5 组的人数记为 ξ ，求 ξ 的分布列和数学期望 . ∴ [80 ， 90) 内的频数为 50 × 0.08 ＝ 4 ， a ＝ 50 － 8 － 20 － 4 － 2 ＝ 16 ； (2) 由题意可知，第 4 组共有 4 人，第 5 组共有 2 人， ∴ 随机变量 ξ 的可能取值为 0 ， 1 ， 2 ， ∴ ξ 的分布列为：