高中数学（人教A版）必修4：1-2-1-2同步试题（含详解） 5页

高中数学(人教 A 版)必修 4 同步试题 1．利用正弦线比较 sin1，sin1.2，sin1.5 的大小关系，有(　　) A．sin1>sin1.2>sin1.5 B．sin1>sin1.5>sin1.2 C．sin1.5>sin1.2>sin 1 D．sin1.2>sin 1>sin 1.5 解析　π 4<1<1.2<1.5<π 2，画图易知． 答案　C 2．若 α 为第二象限角，则下列各式恒小于零的是(　　) A．sinα＋cosα　　　　　　　 B．tanα＋sinα C．cosα－tanα D．sinα－tanα 解析　由 α 为第二象限角知， sinα>0，tanα<0，由三角函数线知|tanα|>sinα. ∴－tanα>sinα，即 sinα＋tanα<0. 答案　B 3．已知 α 是第三象限角，则下列等式中可能成立的是(　　) A．sinα＋cosα＝1.2 B．sinα＋cosα＝－0.9 C．sinαcosα＝ 3 D．sinα＋cosα＝－1.2 解析　画出角 α 的三角函数线易知，sinα＋cosα<－1. 答案　D 4．已知 θ 为锐角，则 sinθ＋cosθ 的值可能是(　　) A.4 3 B.3 5 C．2 D.1 2 解析　由 θ 为锐角知，sinθ＋cosθ>1，但 sinθ＋cosθ≤ 2.故选 A. 答案　A 5．若 0≤θ<2π，且不等式 cosθcosθ，且 sinθ>tanθ.故选 B. 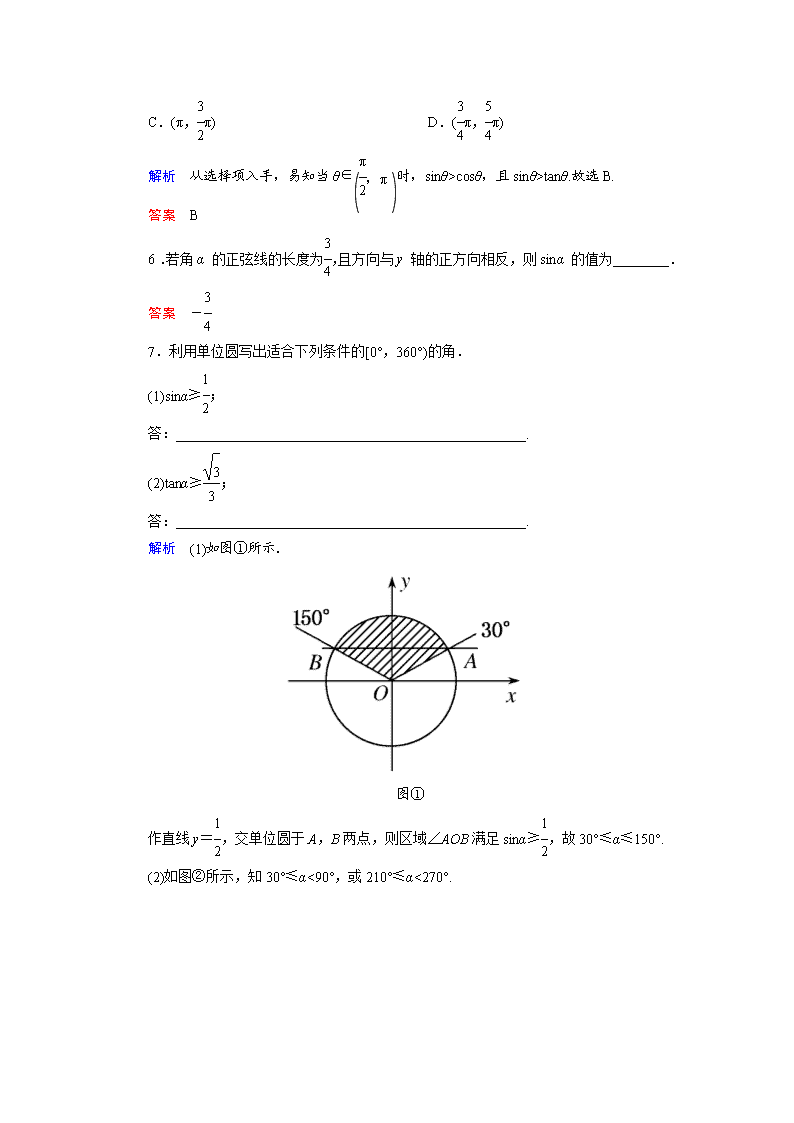答案　B 6 ． 若 角 α 的 正 弦 线 的 长 度 为3 4， 且 方 向 与 y 轴 的 正 方 向 相 反 ， 则 sinα 的 值 为 ________． 答案　－3 4 7．利用单位圆写出适合下列条件的[0°，360°)的角． (1)sinα≥1 2； 答：__________________________________________________. (2)tanα≥ 3 3 ； 答：__________________________________________________. 解析　(1)如图①所示． 图① 作直线 y＝1 2，交单位圆于 A，B 两点，则区域∠AOB 满足 sinα≥1 2，故 30°≤α≤150°. 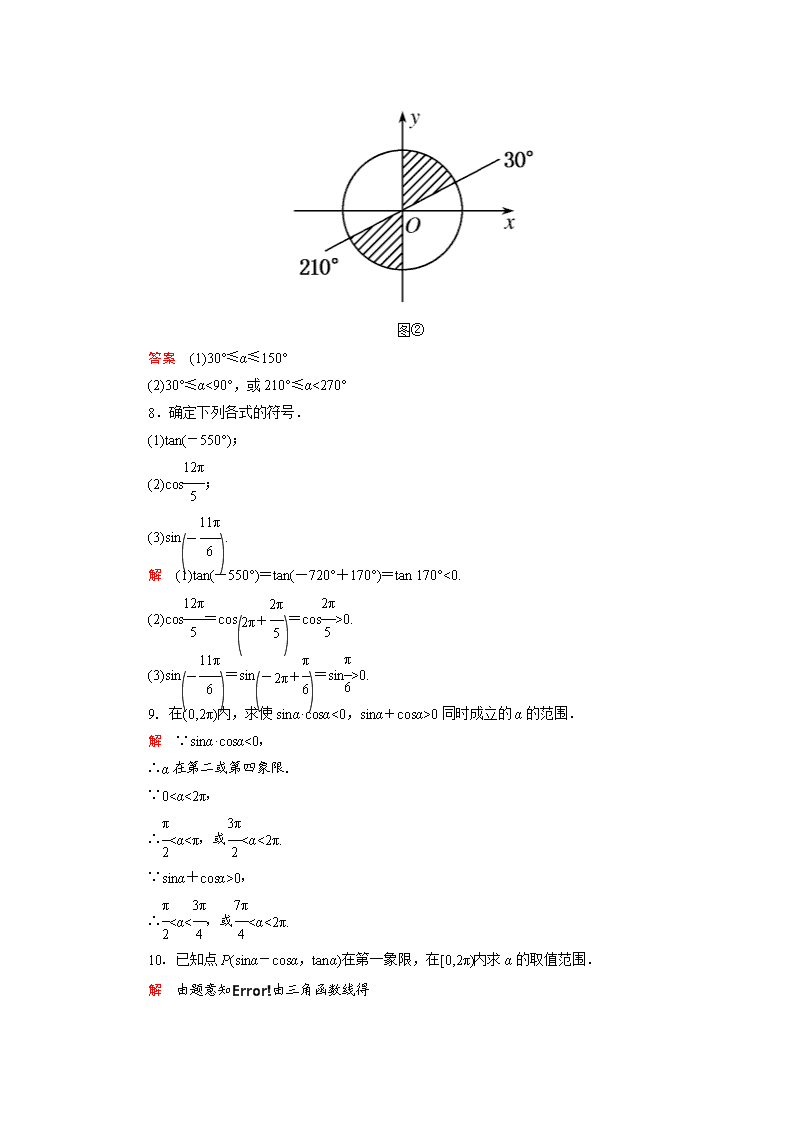(2)如图②所示，知 30°≤α<90°，或 210°≤α<270°. 图② 答案　(1)30°≤α≤150° (2)30°≤α<90°，或 210°≤α<270° 8．确定下列各式的符号． (1)tan(－550°)； (2)cos12π 5 ； (3)sin(－11π 6 ). 解　(1)tan(－550°)＝tan(－720°＋170°)＝tan 170°<0. (2)cos12π 5 ＝cos(2π＋2π 5 )＝cos2π 5 >0. (3)sin(－11π 6 )＝sin(－2π＋π 6)＝sinπ 6>0. 9．在(0,2π)内，求使 sinα·cosα<0，sinα＋cosα>0 同时成立的 α 的范围． 解　∵sinα·cosα<0， ∴α 在第二或第四象限． ∵0<α<2π， ∴π 2<α<π，或3π 2 <α<2π. ∵sinα＋cosα>0， ∴π 2<α<3π 4 ，或7π 4 <α<2π. 10．已知点 P(sinα－cosα，tanα)在第一象限，在[0,2π)内求 α 的取值范围． 解　由题意知Error!由三角函数线得 Error! ∴π 4<α<π 2，或 π<α<5π 4 . 教师备课资源 1.已知 MP，OM，AT 分别是 60°角的正弦线，余弦线，正切线，则一定有(　　) A．MP0. ∵π 2<2<π，∴cos2<0. ∴－3cos2>0. ∴角 α 是第一象限角． 答案　一 4．若角 α 的终边与直线 y＝3x 重合，且 sinα<0，又 P(m，n)是角 α 终边上一点，且|OP| ＝ 10，则 m－n 等于________． 解析　由 sinα＝ n 10<0，知 n<0. 又 P(m，n)在直线 y＝3x 上， ∴n＝3m<0，∴m<0. 又|OP|＝ m2＋n2＝ 10， ∴m2＋n2＝10,10m2＝10. ∴m＝－1，n＝－3. ∴m－n＝－1－(－3)＝2. 答案　2 5．已知π 4OP－MP，即 cosx>1－sinx. 又 AT>OA，∴tanx>1. ∴tanx>cosx>1－sinx. ∴2tanx>2cosx>21－sinx， 即 c>b>a.