2020-2021学年高一数学单元知识梳理：函数的概念与性质 8页

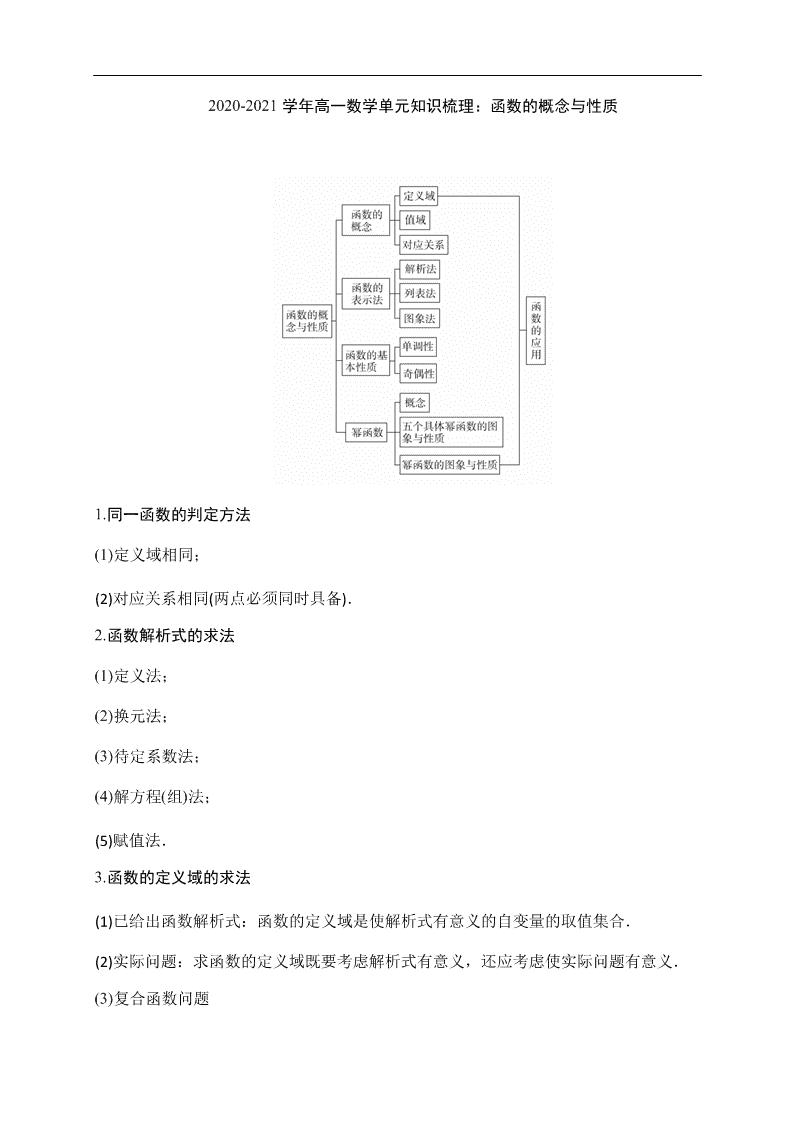
2020-2021 学年高一数学单元知识梳理：函数的概念与性质 1.同一函数的判定方法 (1)定义域相同； (2)对应关系相同(两点必须同时具备)． 2.函数解析式的求法 (1)定义法； (2)换元法； (3)待定系数法； (4)解方程(组)法； (5)赋值法． 3.函数的定义域的求法 (1)已给出函数解析式：函数的定义域是使解析式有意义的自变量的取值集合． (2)实际问题：求函数的定义域既要考虑解析式有意义，还应考虑使实际问题有意义． (3)复合函数问题 ①若函数 f(x)的定义域为[a，b]，函数 f[g(x)]的定义域应由 a≤g(x)≤b 解出； ②若函数 f[g(x)]的定义域为[a，b]，则函数 f(x)的定义域为函数 g(x)在[a，b]上的值域． 注意：①函数 f(x)中的 x 与函数 f[g(x)]中的 g(x)地位相同． ②定义域所指永远是 x 的范围． 4.函数值域的求法 (1)配方法(二次或四次)； (2)判别式法； (3)换元法； (4)函数的单调性法． 5.判断函数单调性的步骤 (1)设 x1，x2 是所研究区间内任意两个自变量的值，且 x10 时，此时 a＋1>1， 由 f(1－a)＝f(1＋a)，得 2(1－a)＋a＝－(1＋a)－2a，解得 a＝－ 2 3 (舍去)； ②当 1－a>1，即 a<0 时，此时 a＋1<1，由 f(1－a)＝f(1＋a)，得－(1－a)－2a＝2(1＋a) ＋a，解得 a＝－ ，符合题意．综上所述，a＝－ . 三、函数的单调性与奇偶性 单调性是函数的一个重要性质，某些数学问题，通过函数的单调性可将函数值间的关系 转化为自变量之间的关系进行研究，从而达到化繁为简的目的，特别是在比较大小、证 明不等式、求值或求最值、解方程(组)等方面应用十分广泛． 奇偶性是函数的又一重要性质，利用奇偶函数图象的对称性可以缩小问题研究的范围， 常能使求解的问题避免复杂的讨论． [典例 3]（2020·邢台市第二中学高一开学考试）设函数 ()yfx 的定义域为 R，并且满足 ( ) ( ) ( )f x y f x f y   ， 1 12f  ，当 0x  时， ()0fx . （1）求 (0)f 的值； （2）判断函数的奇偶性； （3）如果 ( ) (2 ) 2f x f x   ，求 x 的取值范围. 【解析】（1）令 0xy，则 (0) (0) (0)f f f，∴ (0) 0f  . （2）令 yx ，得 (0)()()0ffxfx ， ∴ ( ) ( )f x f x   ，故函数 ()fx是 R 上的奇函数. （3）任取 12,Rxx 且 12xx ，则 210xx. ∵    21f x f x     2111fxxxfx      2111fxxfxfx  21 0f x x   ， ∴    12f x f x  .故 是 上的增函数. ∵ 1 12f  ，∴   1111122222ffff  ， ()(2)2fxfx  ∴  ( ) (2 ) ( (2 ) (2 2) (1)f x f x f x x f x f        . 又由 ()yfx 是定义在 上的增函数，得 221x ，解得 2 1x  四、函数图象及应用 函数的图象是函数的重要表示方法，它具有明显的直观性，通过函数的图象能够掌握函 数重要的性质，如单调性、奇偶性等．反之，掌握好函数的性质，有助于函数图象正确 地画出．函数图象广泛应用于解题过程中，利用数形结合解题具有直观、明了、易懂的 优点． [典例 4] 设函数 f(x)＝x2－2|x|－1(－3≤x≤3)． (1)证明：函数 f(x)是偶函数； (2)画出这个函数的图象； (3)指出函数 f(x)的单调区间，并说明在各个单调区间上 f(x)的单调性； (4)求函数的值域． 【解析】(1)证明：∵函数 f(x)的定义域关于原点对称， 且 f(－x)＝(－x)2－2|－x|－1 ＝x2－2|x|－1＝f(x)， 即 f(－x)＝f(x)，∴f(x)是偶函数． (2)当 0≤x≤3 时， f(x)＝x2－2x－1＝(x－1)2－2. 当－3≤x<0 时，f(x)＝x2＋2x－1＝(x＋1)2－2. 即 f(x)＝      )03(2)1( )30(,2)1( 2 2 xx xx 根据二次函数的作图方法，可得函数图象如下图． (3)函数 f(x)的单调区间为[－3，－1)，[－1,0)，[0,1)，[1,3]． f(x)在区间[－3，－1)和[0,1)上单调递减， 在[－1,0)和[1,3]上单调递增． (4)当 0≤x≤3 时，函数 f(x)＝(x－1)2－2 的最小值为－2，最大值为 f(3)＝2； 当－3≤x<0 时，函数 f(x)＝(x＋1)2－2 的最小值为－2，最大值为 f(－3)＝2.故函数 f(x) 的值域为[－2,2]. 五、幂函数的图象问题 对于给定的幂函数图象，能从函数图象的分布、变化趋势、对称性等方面研究函数的定 义域、值域、单调性、奇偶性等性质．注意图象与函数解析式中指数的关系，能够根据 图象比较指数的大小． [典例 5] 如图是幂函数 y＝xa，y＝xb，y＝xc，y＝xd 在第一象限内的图象，则 a，b，c， d 的大小关系为( ) A.a