高中数学：二《平行线分线段成比例定理》素材1（新人教A版选修4-1） 3页

平行线分线段成比例定理 一、把学生认知结构中原有的知识作为数学教学的出发点 数学学习过程，实质上是数学认知结构的发展变化过程。在任何情况下，已有的认知结构总是学习新知识的基础。数学学习的重要策略就在于建立新知识与原有认知结构之间的联系。我们知道，平行线分线段成比例定理是平行线等分线段定理的推广，而这两节课研究问题的思路基本相同。因而在本课的教学中笔者采用“以旧导新”的方法进行，即通过复习旧知识，探索完善旧知识结构，类比推广导出新知。‎ ‎1．学生1用如下的课件通过广播教学的形式主持复习:‎ 生1：前面我们学过平行线等分线段定理，哪位同学能叙述定理的内容？‎ 生2：如果一组平行线在一条直线上截得的线段相等，那么在其它直线上截得的线段也相等。‎ 生1：很好，请坐（点击“定理”按纽，屏幕呈现平行线等分线段定理内容）。我们连结线段AC、CG、GE、EA、和BF，得到一个什么图形？（边问边在计算机上将上述线段用红线连结）‎ 生众：梯形。‎ 生1：好，根据平行线等分线段定理，我们可以得出有关梯形的推论，哪位同学能叙述呢？‎ 生3：经过梯形一腰的中点与底平行的直线，必平分另一腰。‎ 生1：对。这就是推论1：经过梯形一腰的中点与底平行的直线，必平分另一腰。‎ 我们再移动直线l5，使E点与A点重合，现在又是什么图形呢？（边问边操作）‎ 生众：三角形。‎ 生1：根据平行线等分线段定理，我们可以得出有关三角形的推论2，哪位同学能叙述呢？‎ 生4：经过三角形一边的中点与另一边平行的直线必平分第三边。‎ 生1：很好。推论2是：经过三角形一边的中点与另一边平行的直线必平分第三边。复习完毕，谢谢！‎ ‎2．教师引导学生类比推广导入新课：‎ 师：我们知道（屏幕显示），如图1，如果l1∥l2∥l3，且AB=BC，那么DE=EF，哪位同学能将这个命题改写成比例的形式？‎ 生5：如果l1∥l2∥l3，且，那么即 ‎ ‎ 师：（移动l2如图2）若 ≠1，那么是否还与相等呢？‎ 生众：相等 师：是否相等，我们通过实验来验证。‎ 二、引入数学实验，突破教学难点 在传统的教学中，平行线分线段成比例定理定理的推出是个难点，教材是通过平行线等分线段定理举例说明它的正确性，学生没有足够体验，很难达到对定理的理解，进而影响了后续知识的掌握。皮亚杰认为：数学是人的计数活动和空间度量活动的反身抽象，离开人的活动是没有数学，也学不懂数学的，所以学习数学的一个很重要的环节是了解数学背景，获得数学经验。本课例根据数学思想发展脉络和学生的认知规律，借助《几何画板》软件，创设问题情境，引入如下数学实验：‎ ‎ 如图3，l1∥l2∥l3，直线 l4、l5被l1、l2、l3所截 ‎1、测算AB= ，BC= ，AC= ，‎ ‎ DE= ， EF= ， DF= ‎ ‎2、测算AB:BC= ,AB:AC= ,BC:AC= ‎ ‎ DE:EF= ,DE:DF= ,EF:DF= ‎ ‎3、观察各对应线段的比值，你能得出什么结论？ ‎ ‎4、分别拖动l2、l5，观察测算数据的变化情况，你能得到什么结论？‎ ‎5、用命题的形式表述结论。‎ ‎6、在图３中拖动l5 可得几种变式图形？画出这些图形。‎ ‎7、类比平行线等分线段定理的推论2，由平行线分线段成比例定理，你能得出什么推论？‎ ‎《几何画板》动态地保持几何关系不变的功能，使学生可以任意拖动每一条直线，而画板的实时测量功能又及时为学生提供了准确的测算数据，学生在实验中拖动l2、l5 ，在不断变化的图形中观察测算数据，归纳发现规律，得出了平行线分线段成比例定理：三条平行线截两条直线，所得对应线段成比例。实现了对知识意义的主动建构，较深刻地理解了所学的内容，彻底改变了以讲授“结果”为主，以“灌输”为特征的数学教学模式，充分体现了教师为主导，学生为主体的教学原则。‎ 三、用运动的观点研究变式图形，深化对定理的认识 几何的精髓就是在不断变化的图形中，研究不变的几何规律。本课例充分利用《几何画板》强大的动态功能，用运动变化的观点，动态地设计几何教学，让图形出来说话，充分调动学生的直觉思维。学生在实验中经过自己的动手操作，从动态中观察、比较、归纳、发现，得出平行线分线段成比例定理之后，再让学生通过不断平移l4或l5 ，得到图4所示的几种最具典型性和代表性的变式图形，深化了学生对定理的认识。‎ 图4‎ 本课例还借助几何画板软件，设计了下图所示课件：‎ 通过动态演示课件，强调“对应”的含义，并介绍结合图形形象记忆定理的方法，使学生对定理有了较深刻和全面的理解。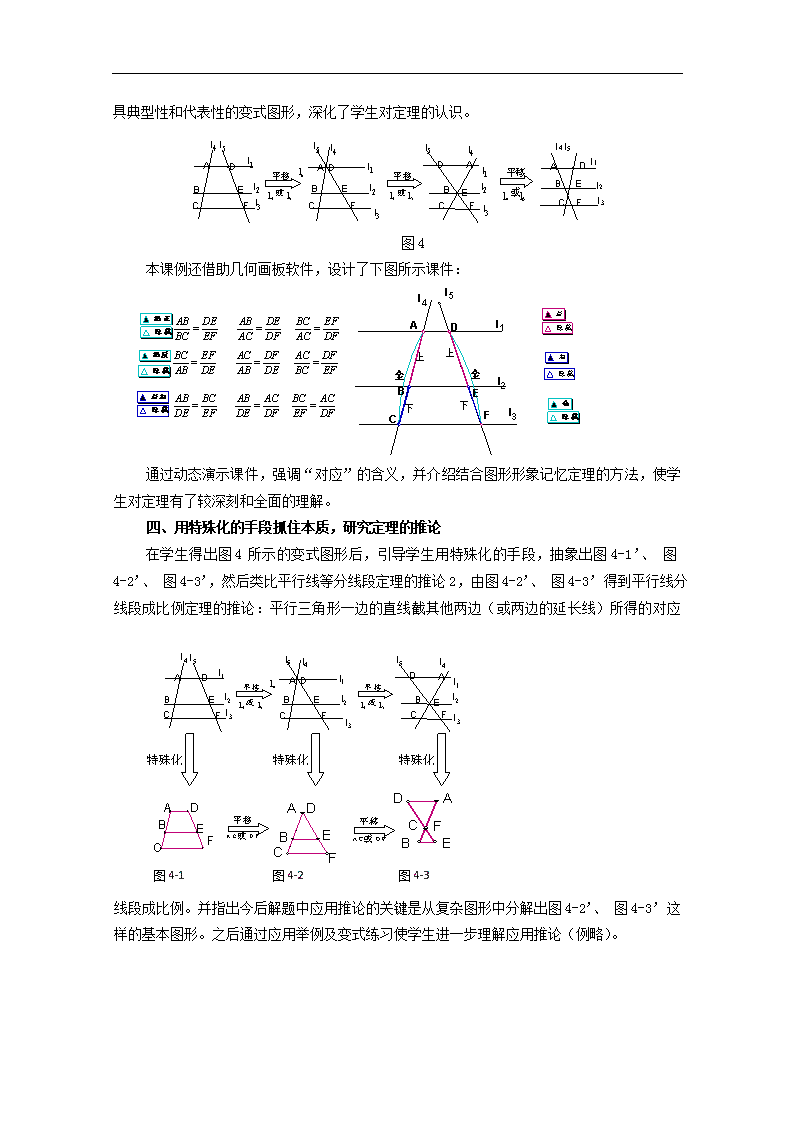‎ 四、用特殊化的手段抓住本质，研究定理的推论 在学生得出图4所示的变式图形后，引导学生用特殊化的手段，抽象出图4‎-1’‎、 图4‎-2’‎、 图4‎-3’‎，然后类比平行线等分线段定理的推论2，由图4‎-2’‎、 图4‎-3’‎得到平行线分线段成比例定理的推论：平行三角形一边的直线截其他两边（或两边的延长线）所得的对特殊化 特殊化 特殊化 图4-1 ‎ 图4-2‎ 图4-3‎ 应线段成比例。并指出今后解题中应用推论的关键是从复杂图形中分解出图4‎-2’‎、 图4‎-3’‎这样的基本图形。之后通过应用举例及变式练习使学生进一步理解应用推论（例略）。‎ w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com