北京市朝阳区2020届高三下学期二模考试数学试题 13页

北京市朝阳区高三年级高考练习二 ‎ 数 学 2020.6‎ ‎（考试时间120分钟 满分150分）‎ 本试卷分为选择题（共40分）和非选择题（共110分）两部分 考生务必将答案答在答题卡上，在试卷上作答无效.考试结束后，将本试卷和答题卡一并交回.‎ 第一部分（选择题 共40分）‎ 一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。‎ ‎（1）在复平面内，复数对应的点位于 ‎（A）第一象限 （B）第二象限 ‎ ‎（C）第三象限 （D）第四象限 ‎ ‎（2）函数的定义域为 ‎(A) (B) (C) (D) ‎ ‎（3）若，，且，则下列不等式一定成立的是 ‎（A） （B） ‎ ‎（C） （D） ‎ ‎（4）圆心在直线上且与轴相切于点的圆的方程是 ‎（A） （B）‎ ‎（C） （D）‎ ‎（5）直线过抛物线的焦点，且与该抛物线交于不同的两点，．若，则弦的长是 ‎ ‎（A） （B） （C） （D）‎ ‎（6）设等差数列的公差为，若，则“”是“为递减数列”的 ‎（A）充分而不必要条件 （B）必要而不充分条件 ‎（C）充分必要条件 （D）既不充分也不必要条件 ‎（7）已知函数，则下列四个结论中正确的是 ‎（A）函数的图象关于中心对称 ‎（B）函数的图象关于直线对称 ‎（C）函数在区间内有个零点 ‎（D）函数在区间上单调递增 ‎（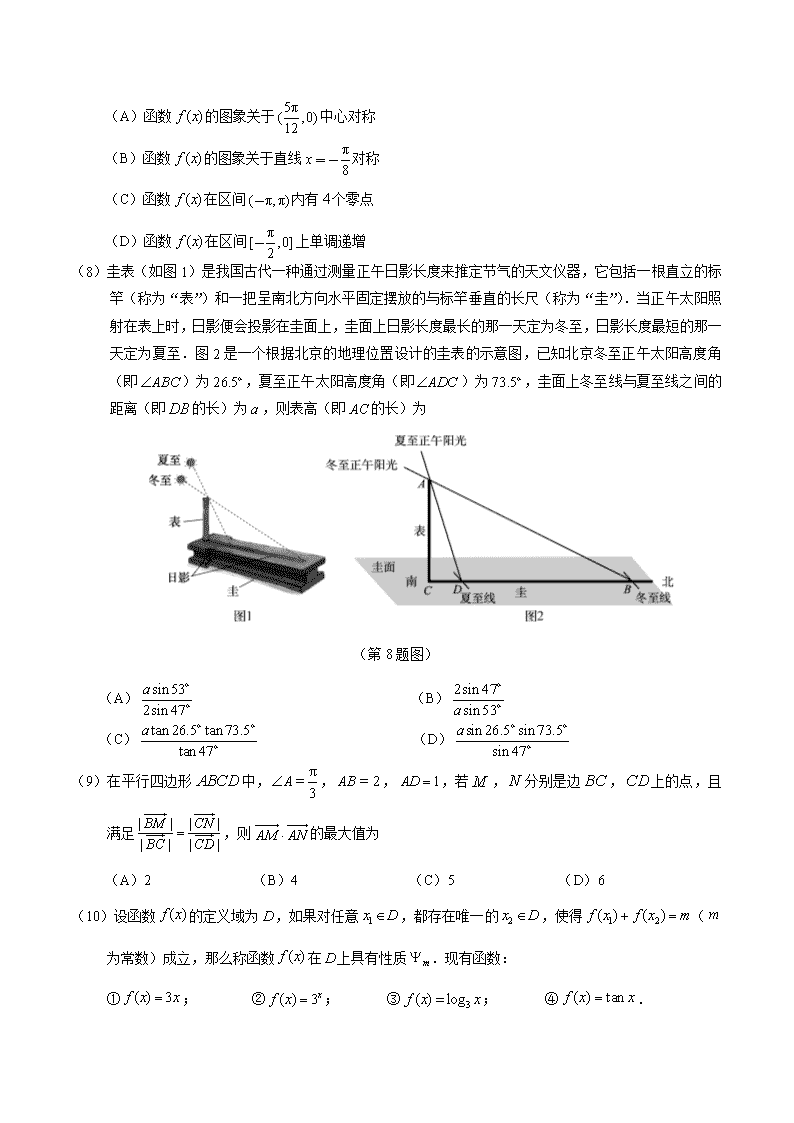8）圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”）．当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．图2是一个根据北京的地理位置设计的圭表的示意图，已知北京冬至正午太阳高度角（即）为，夏至正午太阳高度角（即）为，圭面上冬至线与夏至线之间的距离（即的长）为，则表高（即的长）为 ‎（第8题图） ‎ ‎ ‎ ‎ ‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎（9）在平行四边形中，，，，若，分别是边，上的点，且满足，则的最大值为 ‎ ‎（A）2 （B）4 （C）5 （D）6‎ ‎（10）设函数的定义域为，如果对任意，都存在唯一的，使得（为常数）成立，那么称函数在上具有性质．现有函数：‎ ‎①； ②； ③； ④． ‎ 其中，在其定义域上具有性质的函数的序号是 ‎ ‎（A）①③ （B） ①④‎ ‎（C）②③ （D） ②④‎ 第二部分（非选择题 共110分）‎ 二、填空题共5小题，每小题5分，共25分。‎ ‎（11）已知平面向量，，若，则________．‎ ‎（12）在的展开式中，常数项为________．（用数字作答）‎ ‎（13）某四棱锥的三视图如图所示，如果网格纸上小正方形的边长为，那么该四棱锥的体积为________．‎ ‎（第13题图）‎ ‎（14）已知双曲线的焦点为，，实轴长为2，则双曲线的离心率是________；若点是双曲线的渐近线上一点，且，则的面积为________．‎ ‎（15）颗粒物过滤效率是衡量口罩防护效果的一个重要指标，计算公式为，其中表示单位体积环境大气中含有的颗粒物数量（单位：），表示经口罩过滤后，单位体积气体中含有的颗粒物数量（单位：）．某研究小组在相同的条件下，对两种不同类型口罩的颗粒物过滤效率分别进行了4次测试，测试结果如图所示．图中点的横坐标表示第种口罩第 次测试时的值，纵坐标表示第种口罩第次测试时的值．‎ ‎（第15题图）‎ ‎ ‎ ‎ ‎ ‎ ‎ 该研究小组得到以下结论：‎ ① 在第1种口罩的4次测试中，第4次测试时的颗粒物过滤效率最高； ‎ ② 在第2种口罩的4次测试中，第3次测试时的颗粒物过滤效率最高；‎ ③ 在每次测试中，第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率高；‎ ④ 在第3次和第4次测试中，第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率低．‎ 其中，所有正确结论的序号是________． ‎ 注：本题给出的结论中，有多个符合题目要求．全部选对得5分，不选或有错选得分，其他得3分．‎ 三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。‎ ‎（16）（本小题14分）‎ 已知是公差为的等差数列，其前项和为，且， ．若存在正整数，使得有最小值．‎ ‎（Ⅰ）求的通项公式；‎ ‎（Ⅱ）求的最小值．‎ 从①，②，③这三个条件中选择符合题意的一个条件，补充在上面问题中并作答．‎ 注：如果选择多个条件分别解答，按第一个解答计分．‎ ‎（17）（本小题14分）‎ 如图，在五面体中，面是正方形，，，，且. ‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求直线与平面所成角的正弦值；‎ ‎（Ⅲ）设是的中点，棱上是否存在点，‎ 使得平面？若存在，求线段 的长；若不存在，说明理由．‎ ‎（18）（本小题14分）‎ 近年来，随着网络、人工智能等技术的发展，无人驾驶技术也日趋成熟．为了尽快在实际生活中应用无人驾驶技术，国内各大汽车研发企业都在积极进行无人驾驶汽车的道路安全行驶测试．某机构调查了部分企业参与测试的若干辆无人驾驶汽车，按照每辆车的行驶里程(单位：万公里)将这些汽车分为组：，，，并整理得到如下的频率分布直方图：‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）该机构用分层抽样的方法，从上述组无人驾驶汽车中随机抽取了辆作为样本．从样本中行驶里程不小于万公里的无人驾驶汽车中随机抽取辆，其中有辆汽车行驶里程不小于万公里，求的分布列和数学期望；‎ ‎（Ⅲ）设该机构调查的所有无人驾驶汽车的行驶里程的平均数为．若用分层抽样的方法从上述组无人驾驶汽车中随机抽取辆作为样本，其行驶里程的平均数为；若用简单随机抽样的方法从上述无人驾驶汽车中随机抽取辆作为样本，其行驶里程的平均数为．有同学认为，你认为正确吗？说明理由．‎ ‎（19）（本小题14分） ‎ 已知椭圆：的离心率为，且椭圆经过点．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）已知过点的直线与椭圆交于不同的两点，，与直线交于点，设，，，求证：为定值．‎ ‎（20）（本小题15分）‎ 已知函数．‎ ‎（Ⅰ）若曲线在点处的切线的斜率为．‎ ‎（ⅰ）求的值；‎ ‎（ⅱ）证明：函数在区间内有唯一极值点；‎ ‎（Ⅱ）当时，证明：对任意，．‎ ‎（21）（本小题14分）‎ 设集合，其中，，，是正整数，记．对于，，若存在整数，满足，则称整除，设是满足整除 的数对的个数．‎ ‎（Ⅰ）若，，写出，的值；‎ ‎（Ⅱ）求的最大值；‎ ‎（Ⅲ）设中最小的元素为，求使得取到最大值时的所有集合．‎ 北京市朝阳区高三年级高考练习二 ‎ 数学 参考答案 2020.6‎ 第一部分（选择题 共40分）‎ 一、选择题（共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项）‎ ‎（1）B （2）B （3）D （4）A　 （5）A ‎ ‎（6）C （7）C （8）D （9）C （10）A ‎ 第二部分（非选择题 共110分）‎ 二、填空题（共5小题，每小题5分，共25分）‎ ‎（11） （12） （13）‎ ‎（14）； （15）②④‎ 三、解答题（共6小题，共85分。解答应写出文字说明、演算步骤或证明过程）‎ ‎（16）（本小题14分）‎ 解：（不可以选择③作为补充条件.）‎ 选择①作为补充条件. ‎ ‎ 解答如下：（Ⅰ）因为，，所以．‎ 所以． ……………4分 ‎（Ⅱ）由（Ⅰ）可知． ‎ 所以． ‎ 因为，所以当或时，取得最小值，最小值为． ‎ 故存在正整数或，使得有最小值，最小值为． ……………14分 选择②作为补充条件. ‎ 解答如下：（Ⅰ）因为，，‎ 所以． ……………4分 ‎（Ⅱ）由（Ⅰ）可知． ‎ 所以．所以当时，取得最小值，最小值为．‎ 故存在正整数，使得有最小值，最小值为． ……………14分 ‎（17）（本小题14分）‎ 解：（Ⅰ）因为是正方形，所以．‎ 又因为，平面，‎ 平面，，‎ ‎ 所以平面． ……………4分 ‎（Ⅱ）由（Ⅰ）知，平面,‎ 所以平面平面．‎ 过点作，垂足为，‎ 则平面．‎ 在平面内，过作，‎ 则．‎ 如图建立空间直角坐标系，‎ 因为，，且，所以，．‎ 则，，，，， ‎ ‎ 所以，，．‎ ‎ 设平面的一个法向量为，‎ 则 即 ‎ 令，则，，于是．‎ ‎ 设直线与平面所成角为，‎ 则．‎ ‎ 所以直线与平面所成角的正弦值为． ……………10分 ‎（Ⅲ）棱上存在点，使得平面，此时．理由如下：‎ 因为，平面，平面，‎ 所以平面．‎ 因为平面，平面平面，‎ 所以．‎ 由（Ⅱ）知，， ．‎ 设，则．‎ 由（Ⅱ）知，平面的一个法向量为．‎ 若平面，则，即，解得，即．‎ 经验证，此时平面．‎ 所以棱上存在点，使得平面，此时． ……………14分 ‎（18）（本小题14分）‎ 解：（Ⅰ）由题意知，，所以． ……………3分 ‎（Ⅱ）组无人驾驶汽车的数量比为，若使用分层抽样抽取辆汽车，‎ 则行驶里程在这一组的无人驾驶汽车有辆，‎ 行驶里程在这一组的无人驾驶汽车有辆．‎ 由题意可知，的所有可能取值为，，．‎ ‎， ， ．‎ 所以的分布列为 所以的数学期望． ……………11分 ‎（Ⅲ）这种说法不正确．理由如下：‎ 由于样本具有随机性，故，是随机变量，受抽样结果影响．‎ 因此有可能更接近，也有可能更接近，‎ 所以不恒成立．‎ 所以这种说法不正确． ……………14分 ‎（19）（本小题14分）‎ 解：（Ⅰ）由题意可知得，．‎ 所以椭圆的方程为． ……………5分 ‎（Ⅱ）由题意可知，直线的斜率存在，设直线的方程为．‎ ‎ 由得所以．‎ ‎ 由得.‎ ‎ 整理得.‎ ‎ 由，得．‎ ‎ 设直线与椭圆的交点，，‎ 则，.‎ ‎ 因为，且，，‎ ‎ ，，‎ ‎ 所以 ‎ .‎ ‎ 因为 ‎，‎ ‎ 所以. ……………14分 ‎（20）（本小题15分）‎ 解：（Ⅰ）（ⅰ）因为，所以．‎ ‎ 因为曲线在点处的切线的斜率为，‎ 所以，即，故．‎ 经检验，符合题意． ……………4分 ‎ （ⅱ) 由（ⅰ）可知，．‎ 设，则．‎ ‎ 令，又，得．‎ ‎ 当时，；当时，，‎ ‎ 所以在内单调递增，在内单调递减．‎ ‎ 又，，，‎ ‎ 因此，当时，，即，此时在区间上无极值点；‎ ‎ 当时，有唯一解，即有唯一解，‎ ‎ 且易知当时，，当时，，‎ ‎ 故此时在区间内有唯一极大值点．‎ ‎ 综上可知，函数在区间内有唯一极值点． ……………10分 ‎（Ⅱ） 因为，设，则． ‎ 令，又，得．且当时，；当时，，‎ 所以在内单调递增，在内单调递减．‎ 当时，，，．‎ ‎（1）当，即时，．‎ 此时函数在内单调递增，；‎ ‎（2）当，即时，因为，，‎ 所以，在内恒成立，而在区间内有且只有一个零点，记为，‎ 则函数在内单调递增，在内单调递减．‎ 又因为，，所以此时．‎ 由（1）（2）可知，当时，对任意，总有． ……………15分 ‎（21）（本小题14分）‎ 解：（Ⅰ）；． ……………4分 ‎（Ⅱ）不妨设．‎ 因为，所以，不能整除．‎ 因为最多有，，，，，六种情况，‎ 而，不满足题意，所以．‎ 当时，，所以的最大值为． ……………9分 ‎（Ⅲ）假设．‎ 由（Ⅱ）可知，当取到最大值时，，，，均能整除．‎ 因为，故，‎ 所以．‎ 设，，则，是的因数，‎ 所以是的因数，且是的因数．‎ 因为，所以，‎ 因为是的因数，所以．‎ 因为是的因数，所以是的因数．‎ 因为，所以，所以，或．‎ 故，或．‎ 所以当取到最大值时，，或． ……………14分