2019届二轮复习　集合与常用逻辑用语课件（28张）（全国通用） 28页

第 1 讲　集合与常用逻辑用语 板块二　练透基础送分小考点 [ 考情考向分析 ] 1. 集合是高考必考知识点，经常以不等式解集、函数的定义域、值域为背景考查集合的运算，近几年有时也会出现一些集合的新定义问题 . 2. 高考中考查命题的真假判断或命题的否定，考查充要条件的判断 . 1.(2018· 全国 Ⅰ ) 已知集合 A ＝ { x | x 2 － x － 2>0} ，则 ∁ R A 等于 A.{ x | － 1< x <2} B .{ x | － 1 ≤ x ≤ 2} C.{ x | x < － 1} ∪ { x | x >2} D.{ x | x ≤ － 1} ∪ { x | x ≥ 2} 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 解析 解析　 ∵ x 2 － x － 2>0 ， ∴ ( x － 2)( x ＋ 1)>0 ， ∴ x >2 或 x < － 1 ，即 A ＝ { x | x >2 或 x < － 1}. 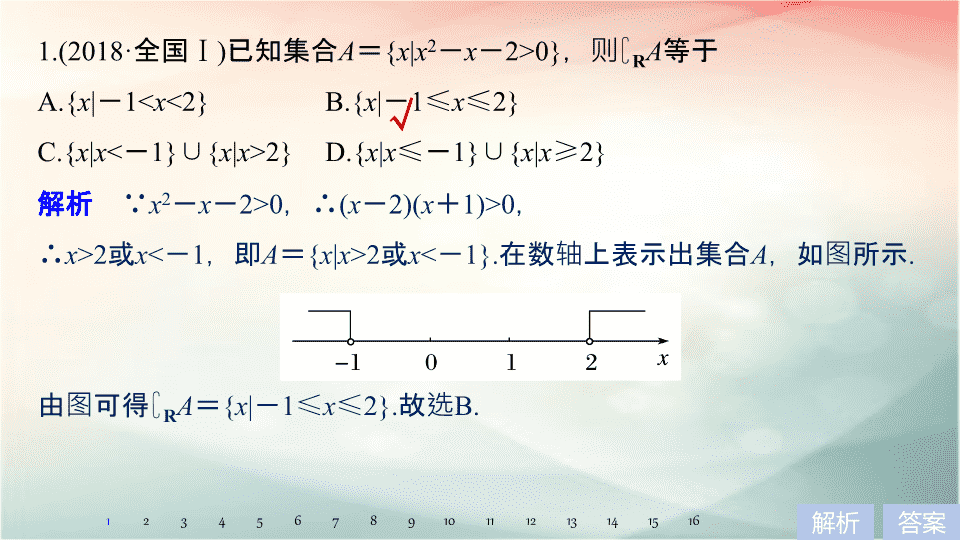在数轴上表示出集合 A ，如图所示 . 由 图可得 ∁ R A ＝ { x | － 1 ≤ x ≤ 2 }. 故 选 B. √ 2.(2018· 安徽省江南十校联考 ) 已知集合 A ＝ { x | y ＝ ln(1 － 2 x )} ， B ＝ { x |e x >1} ，则 A. A ∪ B ＝ { x | x >0} B. A ∩ B ＝ C. A ∩ ∁ R B ＝ D.( ∁ R A ) ∪ B ＝ R 答案 解析 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 3. A ， B ， C 三个学生参加了一次考试， A ， B 的得分均为 70 分， C 的得分为 65 分 . 已知命题 p ：若及格分低于 70 分，则 A ， B ， C 都没有及格 . 在下列四个命题中，为 p 的逆否命题的是 A. 若及格分不低于 70 分，则 A ， B ， C 都及格 B. 若 A ， B ， C 都及格，则及格分不低于 70 分 C. 若 A ， B ， C 至少有一人及格，则及格分不低于 70 分 D. 若 A ， B ， C 至少有一人及格，则及格分高于 70 分 答案 解析 √ 解析　 根据原命题与它的逆否命题之间的关系知，命题 p ：若及格分低于 70 分，则 A ， B ， C 都没有及格， p 的逆否命题是：若 A ， B ， C 至少有 1 人及格，则及格分不低于 70 分 . 故选 C. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 4.(2018· 长春模拟 ) 设命题 p ： ∀ x ∈ (0 ，＋ ∞ ) ， ln x ≤ x － 1 ，则 綈 p 是 A. 綈 p ： ∀ x ∈ (0 ，＋ ∞ ) ， ln x > x － 1 B. 綈 p ： ∀ x ∈ ( － ∞ ， 0] ， ln x > x － 1 C. 綈 p ： ∃ x 0 ∈ (0 ，＋ ∞ ) ， ln x 0 > x 0 － 1 D. 綈 p ： ∃ x 0 ∈ (0 ，＋ ∞ ) ， ln x 0 ≤ x 0 － 1 答案 √ 解析 解析　 因为全称命题的否定是特称 ( 存在性 ) 命题， 所以命题 p ： ∀ x ∈ (0 ，＋ ∞ ) ， ln x ≤ x － 1 的否定 綈 p 为 ∃ x 0 ∈ (0 ，＋ ∞ ) ， ln x 0 > x 0 － 1. 故选 C. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 6. 有关命题的说法正确的是 A. 命题 “ 若 xy ＝ 0 ，则 x ＝ 0 ” 的否命题为： “ 若 xy ＝ 0 ，则 x ≠ 0 ” B. 命题 “ ∃ x 0 ∈ R ，使得 2 x － 1<0 ” 的否定是： “ ∀ x ∈ R ， 2 x 2 － 1<0 ” C. “ 若 x ＋ y ＝ 0 ，则 x ， y 互为相反数 ” 的逆命题为真命题 D. 命题 “ 若 cos x ＝ cos y ，则 x ＝ y ” 的逆否命题为真命题 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 对于 A 选项，命题 “ 若 xy ＝ 0 ，则 x ＝ 0 ” 的否命题为 “ 若 xy ≠ 0 ，则 x ≠ 0 ” ，否命题是条件和结论的双重否定，故 A 错误 ； 对于 B 选项，命题 “ ∃ x 0 ∈ R ，使 2 x － 1<0 ” 的否定是 “ ∀ x ∈ R ,2 x 2 － 1 ≥ 0 ” ，故 B 错误 ； 选项 C 的逆命题为真命题，故 C 正确 ； 选项 D 的原命题是假命题，则逆否命题与之对应也是假命题，故 D 错误，故选 C. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 7.(2018· 天津 ) 设 x ∈ R ，则 “ ” 是 “ x 3 <1 ” 的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 由 x 3 <1 ，得 x <1 ， 当 x ≤ 0 时， 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 8.(2018· 山东枣庄市第三中学调研 ) 若 f ( x ) ＝ sin(2 x ＋ θ ) ，则 “ f ( x ) 的图象 关于 x ＝ 对称 ” 是 “ θ ＝ ” 的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 9 .(2018· 武汉调研 ) 给出下列两个命题 ： p 1 ： ∃ x 0 ∈ R ， 3sin x 0 ＋ 4cos x 0 ＝ 3 ； p 2 ：若 lg a 2 ＋ 2lg b ＝ 0 ，则 a ＋ b ≥ 2 ，那么下列命题为真命题的是 A. p 1 ∧ p 2 B. p 1 ∨ ( 綈 p 2 ) C. p 1 ∨ p 2 D .( 綈 p 1 ) ∧ p 2 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 因为 3sin x ＋ 4cos x ＝ 5sin( x ＋ φ ) ∈ [ － 5 ， 5] ， 对于 p 2 ，由题设有 a 2 b 2 ＝ 1 ， b >0 ，所以 ab ＝ 1 或 ab ＝－ 1 ， 所以 p 1 ∨ ( 綈 p 2 ) 为真命题，故选 B. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 10.(2018· 漳州调研 ) 已知命题 p ：椭圆 25 x 2 ＋ 9 y 2 ＝ 225 与双曲线 x 2 － 3 y 2 ＝ 12 有相同的焦点；命题 q ：函数 f ( x ) ＝ 的 最小值 为 ， 下列命题为真命题的是 A. p ∧ q B .( 綈 p ) ∧ q C. 綈 ( p ∨ q ) D. p ∧ ( 綈 q ) 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 所以 ( 綈 p ) ∧ q 为真命题，故选 B. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 11. 用 C ( A ) 表示非空集合 A 中的元素个数 ， 定义 A * B ＝ 若 A ＝ {1,2} ， B ＝ { x |( x 2 ＋ ax )( x 2 ＋ ax ＋ 2) ＝ 0} ，且 A * B ＝ 1 ，设实数 a 的所有 可能 取值 构成的集合是 S ，则 C ( S ) 等于 A.4 B.3 C.2 D.1 答案 解析 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 　 由 A ＝ {1,2} ，得 C ( A ) ＝ 2 ， 由 A * B ＝ 1 ，得 C ( B ) ＝ 1 或 C ( B ) ＝ 3. 由 ( x 2 ＋ ax )( x 2 ＋ ax ＋ 2) ＝ 0 ， 得 x 2 ＋ ax ＝ 0 或 x 2 ＋ ax ＋ 2 ＝ 0. 当 C ( B ) ＝ 1 时，方程 ( x 2 ＋ ax )( x 2 ＋ ax ＋ 2) ＝ 0 只有实根 x ＝ 0 ，这时 a ＝ 0 ； 当 C ( B ) ＝ 3 时，必有 a ≠ 0 ，这时 x 2 ＋ ax ＝ 0 有两个不相等的实根 x 1 ＝ 0 ， x 2 ＝－ a ，方程 x 2 ＋ ax ＋ 2 ＝ 0 必有两个相等的实根，且异于 x 1 ＝ 0 ， x 2 ＝－ a . 由 Δ ＝ a 2 － 8 ＝ 0 ，得 a ＝ ± 2 ， 可验证均满足题意，故 S ＝ { － 2 ， 0,2 } ，故 C ( S ) ＝ 3. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 12. 已知集合 A ＝ { x | x >2} ，集合 B ＝ { x | x >3} ，以下命题正确的个数是 ① ∃ x 0 ∈ A ， x 0 ∉ B ； ② ∃ x 0 ∈ B ， x 0 ∉ A ； ③ ∀ x ∈ A 都有 x ∈ B ； ④ ∀ x ∈ B 都有 x ∈ A . A.4 B.3 C.2 D.1 答案 解析 √ 解析　 因为 A ＝ { x | x >2} ， B ＝ { x | x >3} ， 所以 B ⊆ A ，即 B 是 A 的子集， ①④ 正确， ②③ 错误，故选 C. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 13. 设全集 U ＝ R ，函数 f ( x ) ＝ lg(| x ＋ 1| ＋ a － 1)( a <1) 的定义域为 A ，集合 B ＝ { x |cos π x ＝ 1} ，若 ( ∁ U A ) ∩ B 恰好有两个元素，则 a 的取值集合为 _________ _ ___. 答案 解析 { a | － 2< a ≤ 0} 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 方法一 　由 | x ＋ 1| ＋ a － 1>0 ，可得 x > － a 或 x < a － 2 ， 故 ∁ U A ＝ [ a － 2 ，－ a ]. 而 B ＝ { x | x ＝ 2 k ， k ∈ Z } ，注意到 [ a － 2 ，－ a ] 关于 x ＝－ 1 对称， 方法二　 由方法一得 ， ∁ U A ＝ [ a － 2 ，－ a ] ， 区间长度为－ a － ( a － 2) ＝ 2 － 2 a ， B ＝ { x | x ＝ 2 k ， k ∈ Z } ， 因为 ( ∁ U A ) ∩ B 恰好有两个元素， 所以 2 ≤ 2 － 2 a <6 ，所以－ 2< a ≤ 0. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 14.(2018· 北京 ) 能说明 “ 若 f ( x )> f (0) 对任意的 x ∈ (0,2] 都成立，则 f ( x ) 在 [0,2] 上是增函数 ” 为假命题的一个函数是 ___________________ _ ____. 解析 答案 f ( x ) ＝ sin x ( 答案不唯一 ) 由正弦函数图象的对称性知，当 x ∈ (0,2] 时， f ( x )> f (0) ＝ sin 0 ＝ 0 ， 故 f ( x ) ＝ sin x 满足条件 f ( x )> f (0) 对任意的 x ∈ (0,2] 都成立，但 f ( x ) 在 [0,2] 上不一直都是增函数 . 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 15. 设命题 p ： |4 x － 3| ≤ 1 ；命题 q ： x 2 － (2 a ＋ 1) x ＋ a ( a ＋ 1) ≤ 0 ，若 綈 p 是 綈 q 的必要不充分条件，则实数 a 的取值范围是 ______________. 解析 答案 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 q ： x 2 － (2 a ＋ 1) x ＋ a ( a ＋ 1) ≤ 0 ， ∴ a ≤ x ≤ a ＋ 1. ∵ 綈 p 是 綈 q 的必要不充分条件， ∴ q 是 p 的必要不充分条件， 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 16. 若 X 是一个集合， τ 是一个以 X 的某些子集为元素的集合，且满足： ① X 属于 τ ， ∅ 属于 τ ； ② τ 中任意多个元素的并集属于 τ ； ③ τ 中任意多个元素的交集属于 τ ，则称 τ 是集合 X 上的一个拓扑 . 已知集合 X ＝ { a ， b ， c } ，对于下面给出的四个集合 τ ： ① τ ＝ { ∅ ， { a } ， { c } ， { a ， b ， c }} ； ② τ ＝ { ∅ ， { b } ， { c } ， { b ， c } ， { a ， b ， c }} ； ③ τ ＝ { ∅ ， { a } ， { a ， b } ， { a ， c }} ； ④ τ ＝ { ∅ ， { a ， c } ， { b ， c } ， { c } ， { a ， b ， c }}. 其中是集合 X 上的一个拓扑的集合 τ 是 ______.( 填序号 ) 解析 答案 ②④ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 ① τ ＝ { ∅ ， { a } ， { c } ， { a ， b ， c }} ，但是 { a } ∪ { c } ＝ { a ， c } ∉ τ ，所以 ① 错； ②④ 都满足集合 X 上的一个拓扑集合 τ 的三个条件 . 所以 ②④ 正确 ； ③ { a ， b } ∪ { a ， c } ＝ { a ， b ， c } ∉ τ ，所以 ③ 错 . 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 本课结束