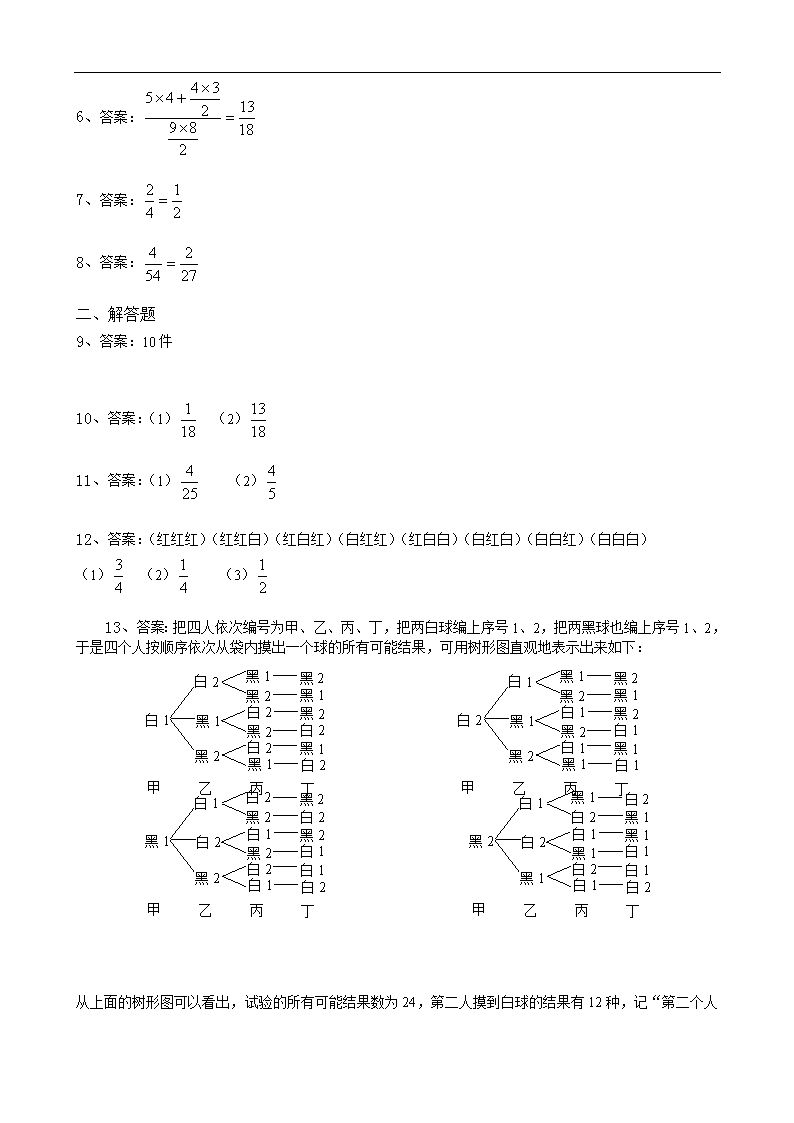高考数学专题复习：《古典概型》同步训练题 4页

‎《古典概型》同步训练题 一、填空题 ‎1、从1,2,3,4,5这5个数中任取两个,则这两个数正好相差1的概率是________。‎ ‎2、一个正方体，它的表面涂满了红色，在它的每个面上切两刀，可得27个小正方体，从中任取一个它恰有一个面涂有红色的概率是 。‎ ‎3、先后抛3枚均匀的硬币,至少出现一次正面的概率为 。‎ ‎4、一个口袋里装有2个白球和2个黑球,这4 个球除颜色外完全相同,从中摸出2个球,则1个是白球,1个是黑球的概率是 。‎ ‎5、同时掷两枚骰子,所得点数之和为5的概率为 ；‎ 点数之和大于9的概率为 。 ‎ ‎6、从标有1,2,3,4,5,6,7,8,9的9张纸片中任取2张,那么这2 张纸片数字之积为偶数的概率为 。 ‎ ‎7、将一枚硬币抛两次,恰好出现一次正面的概率是 。‎ ‎8、从一副扑克牌(54张)中抽一张牌，抽到牌“K”的概率是 。‎ 二、解答题 ‎9、设有一批产品共100件，现从中依次随机取2件进行检验，得出这两件产品均为次品的概率不超过1%，问这批产品中次品最多有多少件？‎ ‎10、连续掷两次骰子，以先后得到的点数为点的坐标，设圆的方程为；‎ ‎（1）求点在圆上的概率； ‎ ‎（2）求点在圆外的概率。‎ ‎11、已知集合，；‎ ‎（1）求为一次函数的概率； ‎ ‎（2）求为二次函数的概率。‎ ‎12、袋中有红、白色球各一个，每次任取一个，有放回地抽三次，写出所有的基本事件，并计算下列事件的概率：‎ ‎（1）三次颜色恰有两次同色； ‎ ‎（2）三次颜色全相同；‎ ‎（3）三次抽取的球中红色球出现的次数多于白色球出现的次数。‎ ‎13、口袋里装有两个白球和两个黑球，这四个球除颜色外完全相同，四个人按顺序依次从中摸出一球，试求“第二个人摸到白球”的概率。‎ 以下是答案 一、填空题 ‎1、答案：‎ ‎2、答案：‎ ‎3、答案：‎ ‎4、答案：‎ ‎5、答案：； ‎ ‎6、答案： ‎ ‎7、答案：‎ ‎8、答案：‎ 二、解答题 ‎9、答案：10件 ‎10、答案：（1） （2）‎ ‎11、答案：（1） （2）‎ ‎12、答案：（红红红）（红红白）（红白红）（白红红）（红白白）（白红白）（白白红）（白白白）‎ ‎（1） （2） （3）‎ ‎13、答案：把四人依次编号为甲、乙、丙、丁，把两白球编上序号1、2，把两黑球也编上序号1、2，于是四个人按顺序依次从袋内摸出一个球的所有可能结果，可用树形图直观地表示出来如下：‎ 黑2‎ 白1‎ 白2‎ 白2‎ 黑1‎ 黑1‎ 黑1‎ 白2‎ 黑1‎ 白1‎ 白1‎ 白2‎ 白2‎ 白1‎ 白1‎ 黑1‎ 甲 乙 丙 丁 白2‎ 白1‎ 黑1‎ 黑2‎ 黑1‎ 黑2‎ 黑2‎ 黑2‎ 黑1‎ 黑1‎ 白1‎ 白1‎ 白1‎ 白1‎ 黑1‎ 黑2‎ 甲 乙 丙 丁 黑1‎ 白1‎ 白2‎ 黑2‎ 白2‎ 黑2‎ 黑2‎ 黑2‎ 白2‎ 白1‎ 白1‎ 白2‎ 白2‎ 白1‎ 白1‎ 黑2‎ 甲 乙 丙 丁 白1‎ 白2‎ 黑1‎ 黑2‎ 黑1‎ 黑2‎ 黑2‎ 黑2‎ 黑1‎ 黑1‎ 白2‎ 白2‎ 白2‎ 白2‎ 黑1‎ 黑2‎ 甲 乙 丙 丁 从上面的树形图可以看出，试验的所有可能结果数为24，第二人摸到白球的结果有12种，记“‎ 第二个人摸到白球”为事件A，则。‎