2019届二轮复习等差数列与等比数列课件（26张）（全国通用） 26页

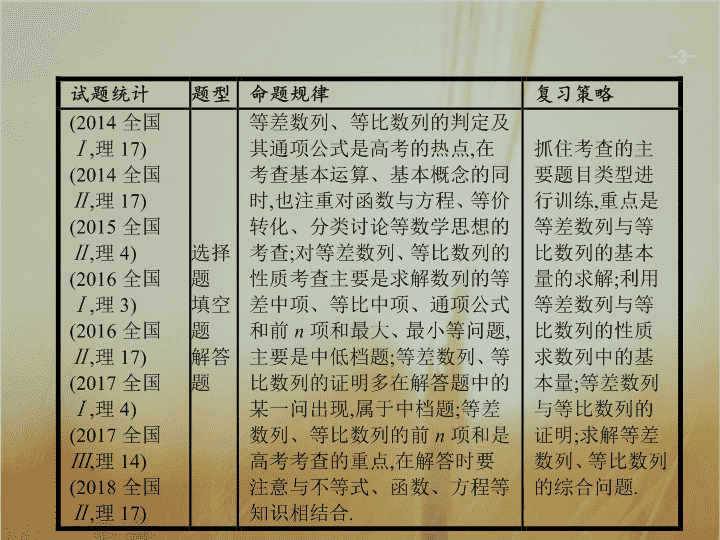
专题四　数列 　等差数列与等比数列 - 3 - - 4 - 命题热点一 命题热点二 命题热点三 命题热点四 等差数列与等比数列的基本量的求解 【思考】 如何求解等差数列与等比数列的基本量? 例 1 记 S n 为等差数列{ a n }的前 n 项和 . 若 a 4 +a 5 = 24, S 6 = 48,则{ a n }的公差为( 　　 ) A . 1 B . 2 C . 4 D . 8 答案 解析 解析 关闭 答案 解析 关闭 - 5 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 等差数列、等比数列的通项公式、求和公式中一共包含 a 1 , n , d ( q ), a n 与 S n 这五个量 . 如果已知其中的三个 , 就可以求其余的两个 . 因为 a 1 , d ( q ) 是两个基本量 , 所以等差数列与等比数列的基本运算问题一般先设出这两个基本量 , 然后根据通项公式、求和公式构建这两者的方程 ( 组 ), 通过解方程 ( 组 ) 求其值 , 这也是方程思想在数列问题中的体现 . - 6 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 1 (1)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( 　　 ) A . 1盏 B . 3盏 C . 5盏 D . 9盏 (2)设等比数列{ a n }满足 a 1 +a 2 =- 1, a 1 -a 3 =- 3,则 a 4 = 　　　　　 .  答案 解析 解析 关闭 答案 解析 关闭 - 7 - 命题热点一 命题热点二 命题热点三 命题热点四 等差数列与等比数列的判定与证明 【思考】 证明数列{ a n }是等差数列或等比数列的基本方法有哪些? 例 2 已知{ a n }是各项均为正数的等差数列,公差为 d. 对任意的 n ∈ N * , b n 是 a n 和 a n+ 1 的等比中项 . 答案 答案 关闭 - 8 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 1 . 证明数列 { a n } 是等差数列的两种基本方法 : (1) 利用定义 , 证明 a n+ 1 -a n ( n ∈ N * ) 为常数 ; (2) 利用等差中项 , 证明 2 a n =a n- 1 +a n+ 1 ( n ≥ 2) . 2 . 证明数列 { a n } 是等比数列的两种基本方法 : - 9 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 2 设 { a n } 和 { b n } 是两个等差数列 , 记 c n = max{ b 1 -a 1 n , b 2 -a 2 n ,…, b n -a n n }( n= 1,2,3,…), 其中 max{ x 1 , x 2 ,…, x s } 表示 x 1 , x 2 ,…, x s 这 s 个数中最大的数 . (1) 若 a n =n , b n = 2 n- 1, 求 c 1 , c 2 , c 3 的值 , 并证明 { c n } 是等差数列 ; (2) 证明 : 或者对任意正数 M , 存在正整数 m , 当 n ≥ m 时 , >M ; 或者存在正整数 m , 使得 c m , c m+ 1 , c m+ 2 ,… 是等差数列 . - 10 - 命题热点一 命题热点二 命题热点三 命题热点四 (1) 解 : c 1 =b 1 -a 1 = 1 - 1 = 0, c 2 = max{ b 1 - 2 a 1 , b 2 - 2 a 2 } = max{1 - 2 × 1,3 - 2 × 2} =- 1, c 3 = max{ b 1 - 3 a 1 , b 2 - 3 a 2 , b 3 - 3 a 3 } = max{1 - 3 × 1,3 - 3 × 2,5 - 3 × 3} =- 2 . 当 n ≥ 3 时 ,( b k+ 1 -na k+ 1 ) - ( b k -na k ) = ( b k+ 1 -b k ) -n ( a k+ 1 -a k ) = 2 -n< 0, 所以 b k -na k 关于 k ∈ N * 单调递减 . 所以 c n = max{ b 1 -a 1 n , b 2 -a 2 n , … , b n -a n n } =b 1 -a 1 n= 1 -n. 所以对任意 n ≥ 1, c n = 1 -n , 于是 c n+ 1 -c n =- 1 . 所以 { c n } 是等差数列 . - 11 - 命题热点一 命题热点二 命题热点三 命题热点四 - 12 - 命题热点一 命题热点二 命题热点三 命题热点四 - 13 - 命题热点一 命题热点二 命题热点三 命题热点四 答案 解析 解析 关闭 答案 解析 关闭 等差数列与等比数列性质的应用 【思考】 常用的等差、等比数列的性质有哪些? - 14 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 等差数列与等比数列的性质多与其下标有关 , 解题需多注意观察 , 发现其联系 , 加以应用 . (1) 等差数列的性质 : ① a n =a m + ( n-m ) d ( n , m ∈ N * ); ② 若 m+n=p+q , 则 a m +a n =a p +a q ( m , n , p , q ∈ N * ); ③ 设等差数列 { a n } 的前 n 项和为 S n , 则 S m , S 2 m -S m , S 3 m -S 2 m , … 也成等差数列 . (2) 等比数列的性质 : ① a n =a m q n-m ( m , n ∈ N * ); ② 若 m+n=p+q , 则 a m · a n =a p · a q ( m , n , p , q ∈ N * ); ③ 若等比数列 { a n } 的公比不为 - 1, 前 n 项和为 S n , 则 S m , S 2 m -S m , S 3 m -S 2 m , … 也成等比数列 . - 15 - 命题热点一 命题热点二 命题热点三 命题热点四 答案 解析 解析 关闭 答案 解析 关闭 - 16 - 命题热点一 命题热点二 命题热点三 命题热点四 等差数列、等比数列的综合问题 【思考】 解决等差数列、等比数列的综合问题的基本思路是怎样的? 例 4 (2018 天津 , 理 18)设{ a n }是等比数列,公比大于0,其前 n 项和为 S n ( n ∈ N * ),{ b n }是等差数列 . 已知 a 1 = 1, a 3 =a 2 + 2, a 4 =b 3 +b 5 , a 5 =b 4 + 2 b 6 . (1)求{ a n }和{ b n }的通项公式; (2)设数列{ S n }的前 n 项和为 T n ( n ∈ N * ), ① 求 T n ; - 17 - 命题热点一 命题热点二 命题热点三 命题热点四 (1) 解 设等比数列 { a n } 的公比为 q. 由 a 1 = 1, a 3 =a 2 + 2, 可得 q 2 -q- 2 = 0 . 因为 q> 0, 可得 q= 2, 故 a n = 2 n- 1 . 设等差数列 { b n } 的公差为 d. 由 a 4 =b 3 +b 5 , 可得 b 1 + 3 d= 4 . 由 a 5 =b 4 + 2 b 6 , 可得 3 b 1 + 13 d= 16, 从而 b 1 = 1, d= 1, 故 b n =n. 所以 , 数列 { a n } 的通项公式为 a n = 2 n- 1 , 数列 { b n } 的通项公式为 b n =n. - 18 - 命题热点一 命题热点二 命题热点三 命题热点四 - 19 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 等差数列和等比数列的综合问题 , 涉及的知识面很宽 , 题目的变化也很多 , 但是只要抓住基本量 a 1 , d ( q ), 充分运用方程、函数、转化等数学思想方法 , 合理运用相关知识 , 就能解决这类问题 . - 20 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练4 等差数列{ a n }的前 n 项和为 S n ,已知 S 10 = 0, S 15 = 25,则 nS n 的最小值为 　　　　　 .   答案 解析 解析 关闭 答案 解析 关闭 - 21 - 规律总结 拓展演练 1 . 等差数列、等比数列的基本运算,一般通过其通项公式与前 n 项和公式构造关于 a 1 与 d 、 a 1 与 q 的方程(组)解决 . 在求解过程中灵活运用等差数列、等比数列的性质,不仅可以快速获解,而且有助于加深对等差数列、等比数列问题的认识 . 2 . 解决等差数列{ a n }前 n 项和问题常用的三个公式 是: ; S n =An 2 +Bn ( A , B 为常数),灵活地选用公式,解决问题更便捷 . 3 . 等差数列和等比数列的中项、前 n 项和都有一些类似的性质,充分利用性质可简化解题过程 . 4 . 证明数列是等差数列或等比数列的基本方法是定义法和中项法 . - 22 - 规律总结 拓展演练 5 . 等差数列、等比数列的通项公式、求和公式有多种形式的变形 . 在求解相关问题时 , 要根据条件灵活选择相关公式 , 同时两种数列可以相互转化 , 如等差数列取指数函数之后即为等比数列 , 正项等比数列取对数函数之后即为等差数列 . 1 . 已知等差数列 { a n } 前 9 项的和为 27, a 10 = 8, 则 a 100 = ( 　　 ) A.100 B.99 C.98 D.97 - 23 - 规律总结 拓展演练 C - 24 - 规律总结 拓展演练 2 . 已知等比数列 { a n } 满足 a 1 = 3, a 1 +a 3 +a 5 = 21, 则 a 3 +a 5 +a 7 = ( 　　 ) A.21 B.42 C.63 D.84 B 3 . (2018 全国 Ⅰ , 理 4) 记 S n 为等差数列 { a n } 的前 n 项和 , 若 3 S 3 =S 2 +S 4 , a 1 = 2, 则 a 5 = ( 　　 ) A .- 12 B .- 10 C . 10 D . 12 B 解析 因为 3 S 3 =S 2 +S 4 , 所以 3 S 3 = ( S 3 -a 3 ) + ( S 3 +a 4 ), 即 S 3 =a 4 -a 3 . 设公差为 d , 则 3 a 1 + 3 d=d , 又由 a 1 = 2, 得 d=- 3, 所以 a 5 =a 1 + 4 d=- 10 . - 25 - 规律总结 拓展演练 4 . 若等差数列{ a n }和等比数列{ b n }满足 a 1 =b 1 =- 1, a 4 =b 4 = 8,则 = 　　　　　 .   1 解析 设等差数列 { a n } 的公差为 d , 等比数列 { b n } 的公比为 q , 由题意知 - 1 + 3 d=-q 3 = 8, - 26 - 规律总结 拓展演练 5 . (2018 全国 Ⅲ , 理 17) 在等比数列 { a n } 中 , a 1 = 1, a 5 = 4 a 3 . (1) 求 { a n } 的通项公式 ; (2) 记 S n 为 { a n } 的前 n 项和 , 若 S m = 63, 求 m.