2018-2019学年黑龙江省双鸭山一中高二下学期开学考试数学（文）试题（Word版） 7页

双鸭山一中 2018--2019 年（下）高二学年开学考试 题 数 学（文科） （考试时间：120 分钟 试卷满分：150 分） 一． 选择题(每小题 5 分，满分 60 分) 1.已知椭圆 x2 a2 ＋y2 2 ＝1 的一个焦点为(2，0)，则椭圆的方程是( ) A.x2 4 ＋y2 2 ＝1 B.x2 3 ＋y2 2 ＝1 C．x2＋y2 2 ＝1 D.x2 6 ＋y2 2 ＝1 2.某单位有职工 750 人，其中青年职工 350 人，中年职工 250 人，老年职工 150 人，为了 了解该单 位职工的健康情况，用分层抽样的方法从中抽取样本. 若样本中的青年职工为 7 人，则样 本容量 为（ ） A.7 B.15 C.25 D.35 3.设实数 yx, 满足约束条件       3 01 01 x yx yx ，错误！未指定书签。则 yxz 23  的最小值 为( ) A.-2 B. 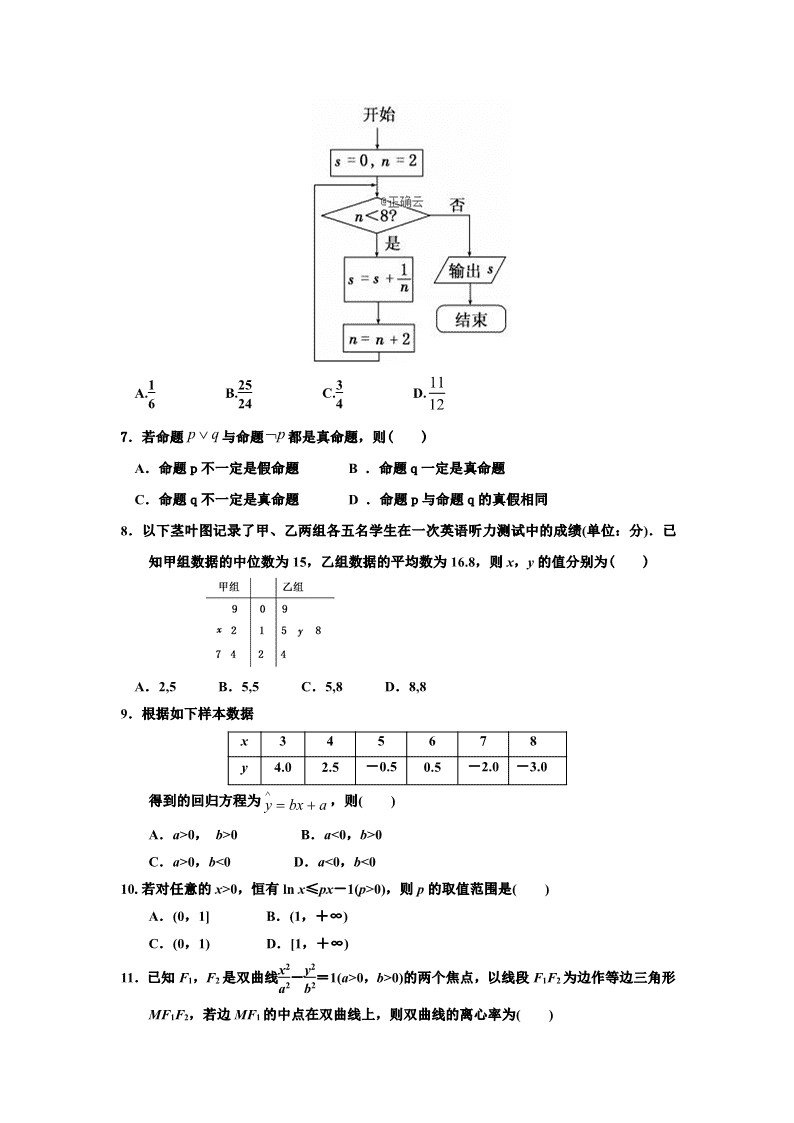1 C.8 D.13 4．设函数 f(x)＝x2 4 －aln x，若 f′(2)＝3，则实数 a 的值为( ) A．4 B．－4 C．2 D．－2 5．下列各进位制数中，最大的数是( ) A．1221(3) B． 11111(2) C．312(4) D．56(8) 6.如图所示，程序框图(算法流程图)的输出结果是( ) A.1 6 B.25 24 C.3 4 D. 12 11 7．若命题 qp  与命题 p 都是真命题，则( ) A．命题 p 不一定是假命题 B ．命题 q 一定是真命题 C．命题 q 不一定是真命题 D ．命题 p 与命题 q 的真假相同 8．以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位：分)．已 知甲组数据的中位数为 15，乙组数据的平均数为 16.8，则 x，y 的值分别为( ) A．2,5 B．5,5 C．5,8 D．8,8 9．根据如下样本数据 x 3 4 5 6 7 8 y 4.0 2.5 －0.5 0.5 －2.0 －3.0 得到的回归方程为 abxy   ，则( ) A．a>0， b>0 B．a<0，b>0 C．a>0，b<0 D．a<0，b<0 10.若对任意的 x>0，恒有 ln x≤px－1(p>0)，则 p 的取值范围是( ) A．(0，1] B．(1，＋∞) C．(0，1) D．[1，＋∞) 11．已知 F1，F2 是双曲线x2 a2 －y2 b2 ＝1(a>0，b>0)的两个焦点，以线段 F1F2 为边作等边三角形 MF1F2，若边 MF1 的中点在双曲线上，则双曲线的离心率为( ) A. 13  B.2 C. 3 D. 12  12．若定义在 R 上的函数 f(x)满足 f(0)＝－1，其导函数 f′(x)满足 f′(x)>k>1，则下列结论中 一定错误的是( ) A．    kf 1 <1 k B．    kf 1 > 1 k－1 C．    1 1 kf < 1 k－1 D．    1 1 kf > k k－1 二．填空题（每题 5 分，满分 20 分） 13.直线 x－y＝2 被圆 x2＋y2＝4 所截得的弦长为________． 14.四边形 ABCD 为长方形，AB＝2，BC＝1，O 为 AB 的中点，在长方形 ABCD 内随机取 一点， 取到的点到 O 的距离大于 1 的概率为________． 15．已知抛物线 xy 22  的焦点是 F，点 P 是抛物线上的动点，又有点 A(3，2)，当|PA|＋ |PF|取最小值时的 P 点坐标为________ 16．如果函数 y＝f(x)的导函数的图象如图所示，给出下列判断中正确的是________ ①函数 y＝f(x)在区间      2 1,3 内单调递增； ②函数 y＝f(x)在区间     3,2 1 内单调递 减； ③函数 y＝f(x)在区间(4,5)内单调递增； ④当 x＝2 时，函数 y＝f(x)有极小值； ⑤当 x＝－1 2 时，函数 y＝f(x)有极大值． 三．解答题（满分 70 分） 17.（10 分）某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进 行试销，得到如下数据： 单价 x（元） 8 8.2 8.4 8.6 8.8 9 销量 y（件） 90 84 83 80 75 68 （Ⅰ）求回归直线方程   axby ，其中 xbyab   ,20 （Ⅱ）预测单价为 10 元时销量为多少件. 18．（12 分）某企业为了解下属某部门对本企业职工的服务情况，随机访问 50 名职工．根 据这 50 名职工对该部门的评分，绘制频率分布直方图(如图所示)，其中样本数据分组 区间为：[40，50)，[50，60)，…，[80，90)，[90，100]． (1)求频率分布直方图中 a 的值； (2)估计该企业的职工对该部门评分不低于 80 的概率； (3)从评分在[40，60)的受访职工中，随机抽取 2 人，求此 2 人的评分都在[40，50)的概 率． 19．（12 分）过点 M(3,2)作圆 O：x2＋y2＋4x－2y＋4＝0 的切线，求切线方程． 20．（12 分）已知函数 f(x)＝x－aln x(a∈R)． (1)当 a＝2 时，求曲线 y＝f(x)在点 A(1，f(1))处的切线方程； (2)求函数 f(x)的极值． 21．（12 分）已知椭圆 E 的中心在坐标原点、对称轴为坐标轴，且抛物线 x2＝－4 2y 的焦 点是它的一个焦点，又点 A(1， 2)在该椭圆上． (1)求椭圆 E 的方程； (2)若斜率为 2的直线 l 与椭圆 E 交于不同的两点 B，C，当△ABC 面积为最大值时， 求直线 l 的方程． 22．（12 分）已知函数 f(x)＝x3－1 2x2＋bx＋c. (1)若 f(x)有极值，求 b 的取值范围； (2)若 f(x)在 x＝1 处取得极值，求证：对[－1，2]内的任意两个值 x1，x2，都有|f(x1)－ f(x2)|≤7 2. 高二开学考试数学（文科）答案 一．选择题 1 2 3 4 5 6 7 8 9 10 11 12 D B A B A D B C C D A C 二．填空题 13. 14. 15. 16.③ 三．解答题 17. (1) （2）50 件 18. （1） （2）0.4 （3） 19.y＝2 或 5x－12y＋9＝0 20. 解：函数f(x)的定义域为(0，＋∞)，f′(x)＝1－a x. (1)当 a＝2 时，f(x)＝x－2ln x，f′(x)＝1－ 2 x(x>0)，因而 f(1)＝1，f′(1)＝－1， 所以曲线 y＝f(x)在点 A(1，f(1))处的切线方程为 y－1＝－(x－1)， 即 x＋y－2＝0. (2)由 f′(x)＝1－ a x＝ x－a x ，x>0 知： ①当 a≤0 时，f′(x)>0，函数 f(x)为(0，＋∞)上的增函数，函数 f(x)无极值； ②当 a>0 时，由 f′(x)＝0，解得 x＝a， 又当 x∈(0，a)时，f′(x)<0；当 x∈(a，＋∞)时，f′(x)>0， 从而函数 f(x)在 x＝a 处取得极小值，且极小值为 f(a)＝a－aln a，无极大值． 综上，当 a≤0 时，函数 f(x)无极值； 当 a>0 时，函数 f(x)在 x＝a 处取得极小值 a－aln a，无极大值． 21.解；(1)由已知抛物线的焦点为(0，－)，故设椭圆方程为 y2 a2＋ x2 a2－2＝1. 将点 A(1，)代入方程，得 2 a2＋ 1 a2－2＝1，整理得 a4－5a2＋4＝0， 解得 a2＝4 或 a2＝1(舍去)，故所求椭圆方程为 y2 4 ＋ x2 2 ＝1. (2)设直线 BC 的方程为 y＝x＋m，设 B(x1，y1)，C(x2，y2)， 代入椭圆方程并化简，得 4x2＋2mx＋m2－4＝0， 由Δ＝8m2－16(m2－4)＝8(8－m2)＞0， 可得 m2＜8 (*) 又 x1＋x2＝－ 2 2m，x1x2＝ m2－4 4 ， 故|BC|＝|x1－x2|＝ 16－2m2 2 . 又点 A 到 BC 的距离为 d＝ |m| 3 . 故 S△ABC＝ 1 2|BC|·d＝ m2（16－2m2） 4 ≤ 1 2· 2m2＋（16－2m2） 2 ＝， 当且仅当 2m2＝16－2m2，即 m＝±2 时取等号(满足(*)式)，S 取得最大值， 此时直线 l 的方程为 y＝x±2. 22.解；(1)f′(x)＝3x2－x＋b，令 f′(x)＝0，由Δ>0 得 1－12b>0，解得 b< 1 12. 即 b 的取值范围为 1 12. (2)∵f(x)在 x＝1 处取得极值，∴f′(1)＝0，∴3－1＋b＝0，得 b＝－2. 令 f′(x)＝0，得 x＝－ 2 3或 x＝1，∴f 2 3＝ 22 27＋c，f(1)＝－ 3 2＋c. 又 f(－1)＝ 1 2＋c，f(2)＝2＋c. ∴f(x)max＝2＋c，f(x)min＝－ 3 2＋c， 故对[－1，2]内的任意两个值 x1，x2， 都有|f(x1)－f(x2)|≤|f(x)min－f(x)max|＝ 3 －（2＋c）＝ 7 2.