2021版高考数学一轮复习核心素养测评五十六圆锥曲线中的定值与定点问题新人教B版 0 10页

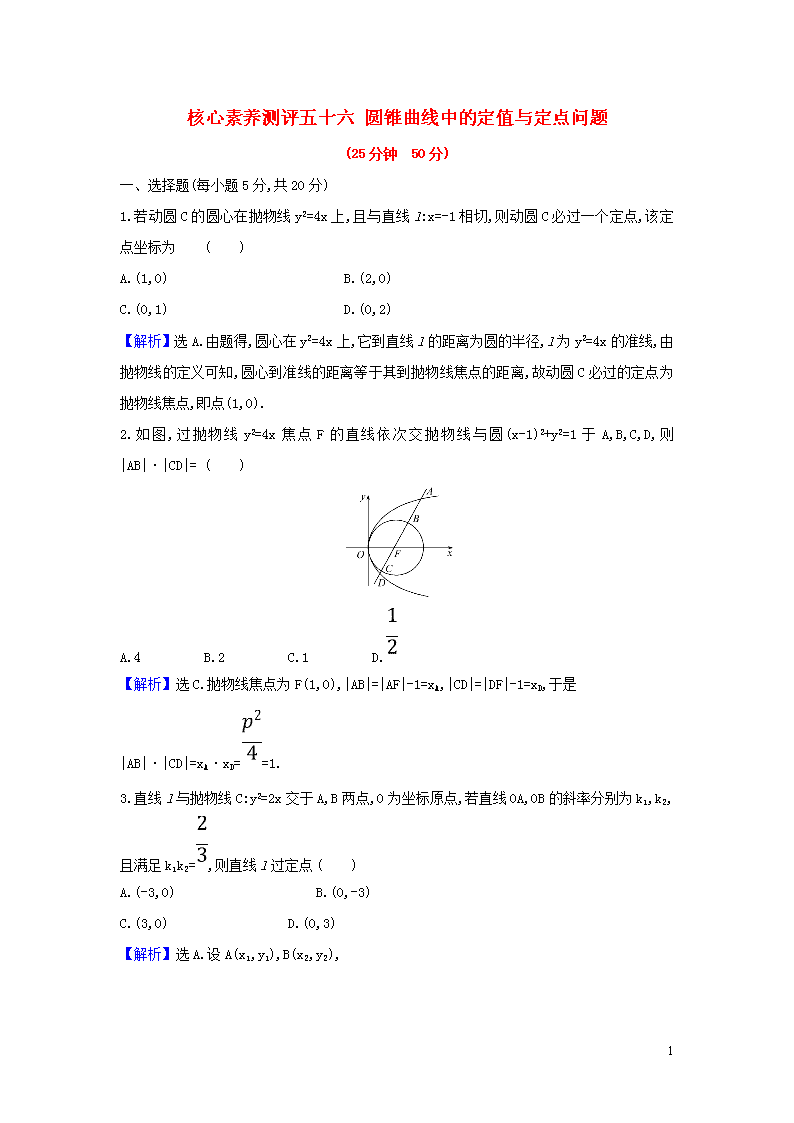
核心素养测评五十六 圆锥曲线中的定值与定点问题 ‎(25分钟　50分)‎ 一、选择题(每小题5分,共20分)‎ ‎1.若动圆C的圆心在抛物线y2=4x上,且与直线l:x=-1相切,则动圆C必过一个定点,该定点坐标为 (　　)‎ A.(1,0) B.(2,0)‎ C.(0,1) D.(0,2) ‎ ‎【解析】选A.由题得,圆心在y2=4x上,它到直线l的距离为圆的半径,l为y2=4x的准线,由抛物线的定义可知,圆心到准线的距离等于其到抛物线焦点的距离,故动圆C必过的定点为抛物线焦点,即点(1,0).‎ ‎2.如图,过抛物线y2=4x焦点F的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则|AB|·|CD|= (　　)‎ A.4 B.2 C.1 D.‎ ‎【解析】选C.抛物线焦点为F(1,0),|AB|=|AF|-1=xA,|CD|=|DF|-1=xD,于是 ‎|AB|·|CD|=xA·xD==1.‎ ‎3.直线l与抛物线C:y2=2x交于A,B两点,O为坐标原点,若直线OA,OB的斜率分别为k1,k2,且满足k1k2=,则直线l过定点 (　　)‎ A.(-3,0) B.(0,-3)‎ C.(3,0) D.(0,3)‎ ‎【解析】选A.设A(x1,y1),B(x2,y2),‎ 10‎ 因为k1k2=,所以·=.‎ 又=2x1,=2x2,所以y1y2=6.‎ 设直线l:x=my+b,代入抛物线C:y2=2x得y2-2my-2b=0,所以y1y2=-2b=6,得b=-3,即直线l的方程为x=my-3,所以直线l过定点(-3,0).‎ ‎4.(多选)如图,已知椭圆C1:+y2=1,过抛物线C2:x2=4y的焦点F的直线交抛物线于M,N两点,连接NO,MO并延长分别交C1于A,B两点,连接AB,△OMN与△OAB的面积分别记为S△O M N,S△OAB.则在下列说法中,正确的是 (　　)‎ A.若记直线NO,MO的斜率分别为k1,k2,则k1k2的大小是定值为-‎ B.△OAB的面积S△OAB是定值1‎ C.线段OA,OB长度的平方和|OA|2+|OB|2是定值5‎ D.设λ=,则λ≥2‎ ‎【解析】选ABCD. 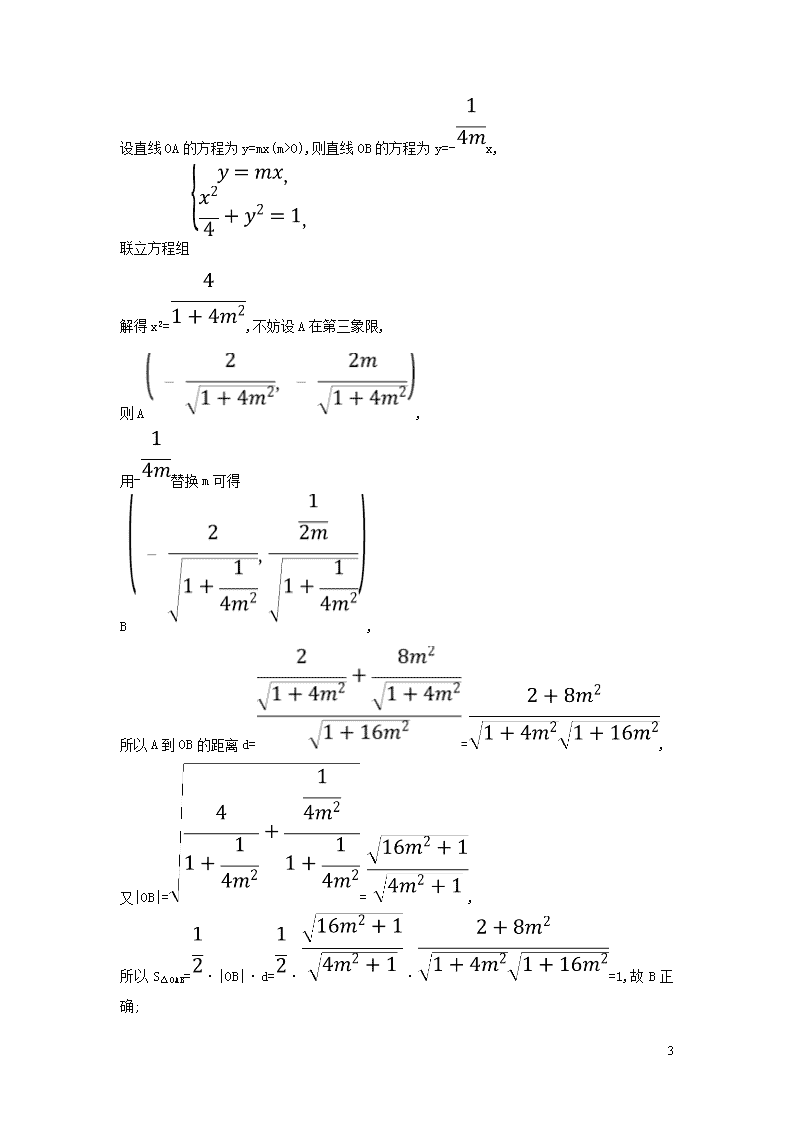F(0,1),设直线MN的方程为y=kx+1,M(x1,y1),N(x2,y2).‎ 联立方程组 消元得:x2-4kx-4=0,所以x1+x2=4k,x1x2=-4,‎ 所以y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1=1,‎ 所以k1k2=·==-,故A正确;‎ 10‎ 设直线OA的方程为y=mx(m>0),则直线OB的方程为y=-x,‎ 联立方程组 解得x2=,不妨设A在第三象限,‎ 则A,‎ 用-替换m可得 B,‎ 所以A到OB的距离d==,‎ 又|OB|==,‎ 所以S△OAB=·|OB|·d=··=1,故B正确;‎ 10‎ 又|OA|2=+=,|OB|2=,‎ 所以|OA|2+|OB|2==5,故C正确;‎ 联立方程组可得x(x-4m)=0,‎ 故N(4m,4m2),所以|ON|=4m,‎ ‎-替换m可得M,‎ 所以M到直线OA的距离h==,‎ 所以S△O M N=·|ON|·h=2m=2m+≥2,当且仅当2m=即m=时取等号.‎ 所以λ==S△OMN≥2,故D正确.‎ 二、填空题(每小题5分,共10分)‎ ‎5.已知曲线P上的点到(2,0)的距离比到直线x=-5的距离小3,直线l1与曲线P交于M(x1,y1),N(x2,y2)两点,点P(x3,y3),Q(x4,y4)在曲线P上,若x1,x2,x3,x4均不相等,且kMP=-kNQ,则kMN+kNP+kPQ+kQM=________.  ‎ ‎【解析】因为曲线P上的点到(2,0)的距离比到直线x=-5的距离小3,所以曲线P上的点到(2,0)的距离与到直线x=-2的距离相等,‎ 故曲线P:y2=8x,则 10‎ kMN===,‎ 同理可得kNP=,kPQ=,‎ kQM=,‎ kMP=,kNQ=,由于kMP=-kNQ,‎ 则=-,可得y1+y2+y3+y4=0,‎ 由此可得=-,即kQM=-kNP,‎ 同理有=-,即kMN=-kPQ,‎ 故kMN+kNP+kPQ+kQM=0.‎ 答案:0‎ ‎6.(2020·西安模拟)已知点A在抛物线C:y2=2px(p>0)的准线上,则抛物线C的方程为________;若点M、N在抛物线C上,且位于x轴的两侧,O是坐标原点,若·=3,动直线MN过定点,定点的坐标是________. ‎ ‎【解析】点A在抛物线C:y2=2px(p>0)的准线上,可得=,解得p=1,所以抛物线C的方程为y2=2x;‎ 设直线MN的方程为ty=x-m.M(x1,y1),N(x2,y2).‎ 联立化为:y2-2ty-2m=0,‎ 所以y1+y2=2t,y1y2=-2m,‎ 10‎ 因为·=3,‎ 所以3=y1y2+x1x2=y1y2+(ty1+m)(ty2+m)=(1+t2)y1y2+mt(y1+y2)+m2,‎ 所以3=-2m(1+t2)+2mt2+m2,‎ 解得m=3或-1(舍去),‎ 所以ty=x-3,‎ 经过定点(3,0).‎ 答案:y2=2x　(3,0)‎ 三、解答题(每小题10分,共20分)‎ ‎7.(2020·北京模拟)已知椭圆C:+y2=1(a>1)的离心率为. ‎ ‎(1)求椭圆C的方程.‎ ‎(2)设直线l过点M(1,0)且与椭圆C相交于A,B两点.过点A作直线x=3的垂线,垂足为D.证明直线BD过x轴上的定点.‎ ‎【解析】(1)由题意可得, 解得a=,b=1,所以椭圆C的方程为+y2=1 .‎ ‎(2)直线BD恒过x轴上的定点(2,0).证明如下:‎ ‎①当直线l斜率不存在时,直线l的方程为x=1,‎ 不妨设A,B,D.‎ 此时,直线BD的方程为:y=(x-2),所以直线BD过定点(2,0).‎ ‎②当直线l的斜率存在时,设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-1),D(3,y1).‎ 由,得:(1+3k2)x2-6k2x+3k2-3=0.‎ 10‎ 所以x1+x2=,x1x2=.…(*)‎ 直线BD的方程为:y-y1=(x-3),只需证明直线BD过点(2,0)即可.‎ 令y=0,得x-3=-,‎ 所以x==‎ ‎=即证=2,‎ 即证2-x1x2=3.‎ 将(*)代入可得2-x1x2=-==3.‎ 所以直线BD过点(2,0),‎ 综上所述,直线BD恒过x轴上的定点(2,0).‎ ‎8.已知椭圆C1:+=1(a>b>0)的离心率为,椭圆C2:+=1(a>b>0)经过点. ‎ ‎(1)求椭圆C1的标准方程.‎ ‎(2)设点M是椭圆C1上的任意一点,射线MO与椭圆C2交于点N,过点M的直线l与椭圆C1有且只有一个公共点,直线l与椭圆C2交于A,B两个相异点,证明:△NAB的面积为定值.‎ ‎【解析】(1)因为C1的离心率为,‎ 10‎ 所以=1-,解得a2=3b2.①‎ 将点代入+=1,‎ 整理得+=1.②‎ 联立①②,得a2=1,b2=,‎ 故椭圆C1的标准方程为x2+=1.‎ ‎(2)①当直线l的斜率不存在时,点M为或,由对称性不妨取M,‎ 由(1)知椭圆C2的方程为+y2=1,‎ 所以有N.‎ 将x=1代入椭圆C2的方程得y=±,‎ 所以S△NAB=·‎ ‎= =+.‎ ‎②当直线l的斜率存在时,设其方程为y=kx+m,‎ 将y=kx+m代入椭圆C1的方程 得x2+6kmx+3m2-1=0,‎ 10‎ 由题意得Δ=-4=0,‎ 整理得3m2=1+3k2.‎ 将y=kx+m代入椭圆C2的方程,‎ 得x2+6kmx+3m2-3=0.‎ 设A,B,‎ 则x1+x2=-,x1x2=,‎ 所以=‎ ‎==.‎ 设M,N,=λ,‎ 则可得x3=-λx0,y3=-λy0.‎ 因为 ,‎ 所以 ,‎ 解得λ=(λ=-舍去),‎ 所以=,‎ 从而=.‎ 又因为点O到直线l的距离为d=,‎ 10‎ 所以点N到直线l的距离为 d=‎ 所以S△NAB=d·‎ ‎=·· ‎ ‎=+.‎ 综上,△NAB的面积为定值+.‎ 10‎