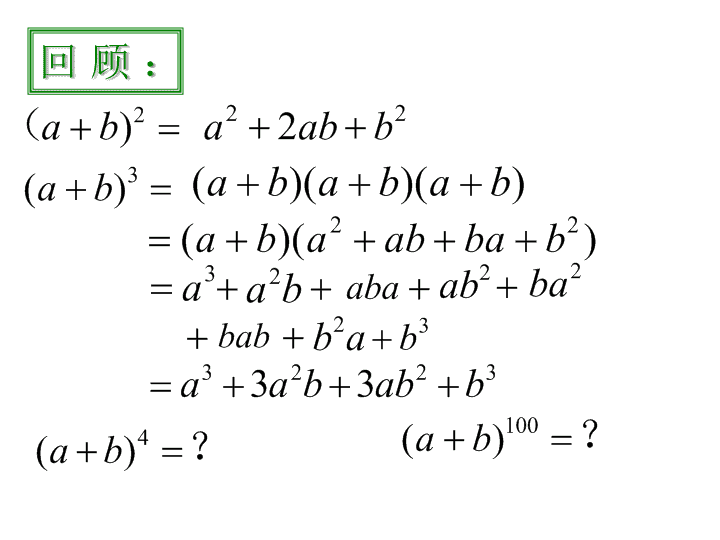高中数学选修2-3教学课件：二项式定理1 16页

二 项 式 定 理 问题 : (1) 今天是星期五，那么 7 天后 (4) 如果是 天后的这一天呢？ 的这一天是星期几呢 ? (2) 如果是 15 天后的这一天呢？ （星期六） （星期五） (3) 如果是 24 天后的这一天呢？ （星期一） 回顾： 观察下面两个公式，从右边的项数、每项的 次数、系数进行研究，你会发现什么规律？ 项数比左边次数多 1 ；每项次数均为 左边指数， a,b 指数 a 降 b 升；系数 尝试二项式定理的发现 : 猜想： (a+b) 4 = (a+b) (a+b) (a+b) (a+b) 展开后，会是什么样呢？你能从项数、次数、系数这几个方面谈一谈吗？ ① 展开式中，每一项是怎样得到的？ ② 既然这样，每一项的次数都应为几次？ （ 4 次） 展开后具有哪些形式的项呢？ (a 4 ， a 3 b ， a 2 b 2 ， ab 3 ， b 4 ) 探索： (a+b) 4 = (a+b) (a+b) (a+b) (a+b) 在上面 4 个括号中： 每个都不取 b ，有 种取法， a 4 的系数 恰有１个取 b ，有 种取法， a 3 b 的系数 ③ 每一项在展开式中出现多少次，也就是展开式中各项 系数为什么？ 恰有２个取 b ，有 种取法， a 2 b 2 的系数 恰有３个取 b ，有 种取法， ab 3 的系数 ４个都取 b ， 有 种取法 , b 4 的系数 因此： 特点： 项数比次数多 1 ；每项次数为左边指数 4 ， a 降 b 升； 系数为 按上述规律，我们能将 (a+b) n 展开吗？ （一）二项式定理： 右边多项式叫 (a+b) n 的二项展开式； 叫二项式系数； 叫二项展开式的通项， 用 T r+1 表示即： T r+1 = 1 、弄清定理结构特征：项数： n+1 次数： n ， a 降 b 升，和为 n 系数： 2 、二项式系数与项的系数不同 二项式系数是组合数，而项的系数是该项的数字因数 3 、①通项公式可用求展开式中任意一项，求时必需 明确 r= ？，一般地，比所说的第几项少 1 ② 通项是针对 (a+b) n 的标准形式而言，而 (b+a) n ， (a-b) n 的通项则分别为 : 注意： 4 、 在定理中，令 a=1 ， b=x ，则 尝试二项式定理的应用： 例 1 ： 尝试二项式定理的应用： 练习： 第三项的系数是 ， 第三项的二项式系数是 。 解 ： 例 2 ：展开 （先化简，再展开） 计算出结果即可 例 3 ：求 (x+a) 12 展开式中倒数第 4 项 分析：倒数第 4 项，是第几项？用通项公式时， r= ？ 解：展开式共 13 项，倒数第 4 项为它的第 10 项 T 9+1 = 例 4 求 展开式中的有理项 解 : 令 原式的有理项为 : 有 常 数 项 吗 ？ 求二项展开式的某一项 , 或者求满足某种条 件的项 , 或者求某种性质的项 , 如含有 x 项 的系数 , 有理项 , 常数项等 , 通常要用到二项 式的通项求解 . 注意 (1) 二项式系数与系数的区别 . (2) 表示第 项 . 3 例题点评 问题探究 : (1) 今天是星期五，那么 7 天后 (4) 如果是 天后的这一天呢？ 的这一天是星期几呢 ? (2) 如果是 15 天后的这一天呢？ （星期五） (3) 如果是 24 天后的这一天呢？ （星期六） （星期一） 问题探究 : 余数是 1 ， 所以是 星期六 (3) 今天是星期五，那么 天后 的这一天是星期几？ 探究： 若将 除以 9 ，则得到的余数是多少？ 所以 余数是 1 ， 思考： 若将 除以 9 ，则得到的余数还是 1 吗？ 1 、二项式定理及结构特征 2 、二项式系数与项系数不同 作用：求任一项；求某一项系数 关键：明确 r 3 、通项公式 T r+1 = 4 、定理特例 小结：