广东省中山大学附中2019-2020学年高二下学期线上期中考试数学试题 4页

‎2019-2020第二学期中大附中高二数学期中线上考试（2020.04.18）‎ 姓名：_____ 班级：_____ 学号：_____ 分数：_____‎ 提醒：（1）时间：15：00-17：00；满分：150分．‎ ‎（2）提交：到截止时间时（17：00），老师会在腾讯课堂和微信答疑群同步提醒停止答题，提交答案（10分钟内提交完成，17：05播放音乐．17：10后未交的0分处理．）‎ ‎（3）提醒：①考试平台：小七学伴；（选择题、非选择题均在此）；‎ ‎②每个题都要标上题号；（即便某一个填空题不会，也要标题号）；‎ ‎③解答题每个题都要能在一张照片拍完；（不管几问）‎ ‎④不接受考完后微信补交，所以提交时要仔细、耐心．‎ 一、单选题（本题共12小题，每小题5分．共60分）‎ ‎1．复数（是虚数单位）在复平面内对应的点在（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．已知复数满足，，则（ ）‎ А． B． C． D．5‎ ‎3．若满足，则（ ）‎ A．0 B．‎1 C． D．‎ ‎4．一个市禁毒宣传讲座要到4个学校开讲，一个学校讲一次，不同的次序种数为（ ）‎ A．4 B． C．24 D．48‎ ‎5．已经知道函数在上，则下列说法不正确的是（ ）‎ A．最大值为9 B．最小值为 C．函数在区间单调递增 D．是它的极大值点 ‎6．若，则（ ）‎ A． B． C． D．‎ ‎7．若离散型随机变量的分布列如下，则的最大值为（ ）‎ ‎0‎ ‎10‎ ‎20‎ A． B． C． D．1‎ ‎8．若的展开式中二项式系数最大的项只有第6项，则展开式的各项系数的绝对值之和为（ ）‎ A． B． C． D．‎ ‎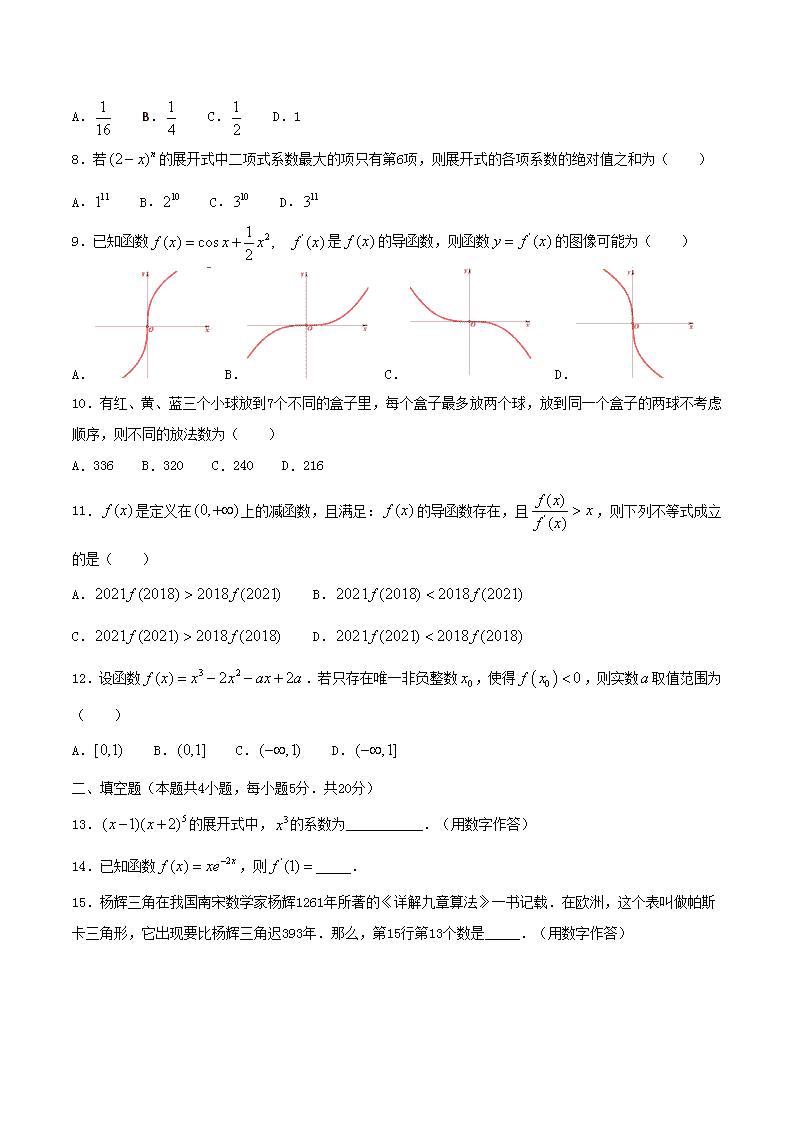9．已知函数是的导函数，则函数的图像可能为（ ）‎ A． B． C． D．‎ ‎10．有红、黄、蓝三个小球放到7个不同的盒子里，每个盒子最多放两个球，放到同一个盒子的两球不考虑顺序，则不同的放法数为（ ）‎ A．336 B．‎320 C．240 D．216‎ ‎11．是定义在上的减函数，且满足：的导函数存在，且，则下列不等式成立的是（ ）‎ A． B．‎ C． D．‎ ‎12．设函数．若只存在唯一非负整数，使得，则实数取值范围为（ ）‎ A． B． C． D．‎ 二、填空题（本题共4小题，每小题5分．共20分）‎ ‎13．的展开式中，的系数为___________．（用数字作答）‎ ‎14．已知函数，则_____．‎ ‎15．杨辉三角在我国南宋数学家杨辉1261年所著的《详解九章算法》一书记载．在欧洲，这个表叫做帕斯卡三角形，它出现要比杨辉三角迟393年．那么，第15行第13个数是_____．（用数字作答）‎ ‎16．若函数在上有两个不同的零点，则实数的取值范围为_____．‎ 三、解答题（本题共6小题，其中第17题10分，其它每题均12分．共70分）‎ ‎17．已知曲线在点处的切线方程为．‎ ‎（1）求的值，以及和的值；‎ ‎（2）求此函数的单调区间．‎ ‎18．盒子内有3个不同的黑球，5个不同的白球．‎ ‎（1）全部取出排成一列，3个黑球两两不相邻的排法有多少种？‎ ‎（2）从中任取6个球，白球的个数不比黑球个数少的取法有多少种？‎ ‎（3）若取一个白球记2分，取一个黑球记1分，从中任取5个球，使总分不少于7分的取法有多少种？‎ ‎19．已知函数．‎ ‎（1）求此函数的极大值，并请直接写出此函数的零点个数；‎ ‎（2）若函数，且此函数在区间内单调递增的，求实数的取值范围．‎ ‎20．某社团现有5名女生，5名男生，其中3名学生来自同一个班，另外7名学生分别来自不同的班级．‎ 现要随机选3名学生参加活动．‎ ‎（1）求“选出的3名学生中，至多有2名来自同一班级”的概率；‎ ‎（2）设选出的3名学生中女生的人数为随机变量，求的分布列．‎ ‎21．某学校科技节需要同学设计一幅矩形纸板宣传画，要求画面的面积为（下图中的阴影部分），画面的上、下各留空白，左、右各留空白．‎ ‎（1）如何设计画面的高与宽的尺寸，才能使整个宣传画所用纸张面积最小？‎ ‎（2）如果按照第一问这样制作整个宣传画，在科技节结束以后，这整个宣传画纸板可再次作为某实验道具，并要求从整个宣传画板的四个角各截取一个相同的小正方形，做成一个长方体形的无盖容器．问截下的小正方形的边长（也就是该容器的高）是多少时，该容器的容积最大？‎ ‎22．已知函数．‎ ‎（1）讨论的单调性；‎ ‎（2）若在区间存在一个，使得成立，求的取值范围．‎