宁夏银川市兴庆区长庆高级中学2019-2020学年高二上学期期末考试数学（理）试卷 含答案 8页

www.ks5u.com 数学试卷（理科）‎ ‎ 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间120分钟。‎ 第Ⅰ卷(选择题　共60分)‎ 一、选择题：(本大题共12个小题，每小题5分，共60分，) ‎ ‎1. 是虚数单位,复数=（ ）‎ A． B． C． D．‎ ‎2.已知函数的导函数是且，则实数的值为（ ）‎ A． B． C． D．4‎ ‎3.用反证法证明命题“已知，，，则中至少有一个不小于0”假设正确是（ ）‎ ‎ A.假设都不大于0 B.假设至多有一个大于0 ‎ ‎ C.假设都大于0 D.假设都小于0‎ ‎4.下面几种推理中是演绎推理的为(　　)‎ A．高二年级有21个班，1班51人，2班53人，三班52人，由此推测各班都超过50人 B．猜想数列，，，…的通项公式为an＝(n∈N＋)‎ C．半径为r的圆的面积S＝πr2，则单位圆的面积S＝π D．由平面三角形的性质，推测空间四面体性质 ‎5.已知函数的导函数为，且满足，则＝(　　)‎ A． ‎-1 B．1 C.-2 D.3‎ ‎6. 等于（ ）‎ A. B. C. 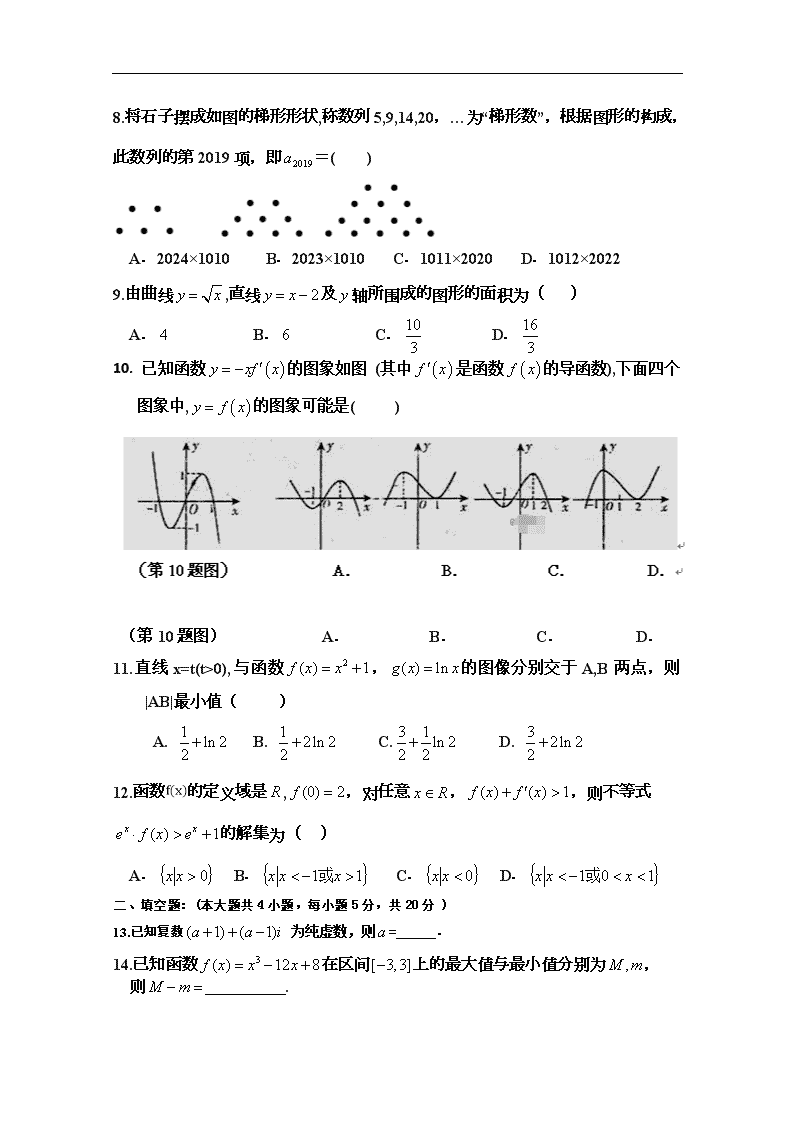D.‎ ‎7.曲线在点处的切线方程为（　　）‎ A． B． C． D．‎ ‎8.将石子摆成如图的梯形形状,称数列5,9,14,20，…为“梯形数”，根据图形的构成，此数列的第2019项，即＝(　　) ‎ A．2024×1010 B．2023×1010 C．1011×2020 D．1012×2022‎ ‎9.由曲线,直线及轴所围成的图形的面积为（ ）‎ A． B． C． D． ‎ ‎10. 已知函数的图象如图 (其中是函数的导函数),下面四个图象中,的图象可能是( )‎ ‎ （第10题图） A． B． C． D．‎ ‎11.直线x=t(t>0),与函数，的图像分别交于A,B两点，则|AB|最小值（ ）‎ A. B. C. D. ‎ ‎12.函数的定义域是,，对任意，，则不等式的解集为（ ）‎ A． B． C． D．‎ 二、填空题: (本大题共4小题，每小题5分，共20分 ) ‎ ‎13.已知复数 为纯虚数，则= ．‎ ‎14.已知函数在区间上的最大值与最小值分别为，‎ 则__________.‎ ‎15.已知，，，，，，经计算得：，，根据以上计算所得规律，可推出 .‎ ‎16. 函数,,若对,,‎ ‎,则实数的最小值是 ．‎ 三、解答题: (本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤)‎ ‎17.(本小题10分)用适当方法证明 ‎（1）求证：.‎ ‎（2）已知求证.‎ ‎18.(本小题12分)已知函数的图象在处的切线方程为．‎ ‎（1）求实数的值. （2）求函数的极值．‎ ‎19.(本小题12分)已知函数在处有极值.‎ ‎（1）求的值和函数的单调区间.‎ ‎（2）求函数在区间上的最值.‎ ‎20.(本小题12分)已知a∈R，函数f(x)＝(－x2＋ax)ex(x∈R)．‎ ‎ (1)当a＝2时，求函数f(x)的单调区间.‎ ‎ (2)若函数f(x)在(－1,1)上单调递增，求a的取值范围．‎ ‎ ‎ ‎21.(本小题12分)已知数列的前项和为，且满足，.‎ ‎（1）写出，，，并推测数列的表达式.‎ ‎（2）用数字归纳法证明（1）中所得的结论.‎ ‎22.(本小题12分)函数，;‎ ‎（1）讨论函数的单调性.‎ ‎（2）若时，函数在上的最大值为1，求的值.‎ 答案 一、 选择题 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ A D D C A D C B D B C A 二、 填空题 ‎13.-1 14.32 15. 16.14‎ 三、 解答题 ‎17.‎ ‎18.（I），‎ ‎，解得；‎ ‎（II）∵∴‎ 由（I）得，令，解得或，‎ 当时，，在上单调递增，‎ 当或时，，在和上单调递减，‎ 所以在处取得极小值，‎ 在处取得极大值 ‎19.（1）‎ 由题意；‎ 所以，定义域为 ‎ 令，单增区间为；‎ 令，单减区间为 ‎（2）由（1）知在区间函数单调递减，在区间函数单调递增，‎ 所以，而，，显然，所以.‎ ‎20.解　当a＝2时，f(x)＝(－x2＋2x)ex，f′(x)＝(－x2＋2)ex.‎ ‎ 当f′(x)>0时，(－x2＋2)ex>0，注意到ex>0，所以－x2＋2>0，解得－0，‎ ‎ 因此－x2＋(a－2)x＋a≥0在(－1,1)上恒成立，‎ ‎ 也就是a≥＝x＋1－在(－1,1)上恒成立．‎ ‎ 设y＝x＋1－，则y′＝1＋>0，即y＝x＋1－在(－1,1)上单调递增，‎ ‎ 则y<1＋1－＝，故a≥.‎ ‎21.【答案】（1），，.（2）见解析 ‎【解析】‎ 分析：（1）利用，代入计算，即可得到的值，猜想；‎ ‎（2）利用数学归纳法进行证明，检验当时等式成立，假设是命题成立，证明当时，命题也成立即可．‎ 详解：（1）将，，分别代入，‎ 可得，，.‎ 猜想.‎ ‎（2）①由（1），得时，命题成立；‎ ‎②假设时，命题成立，即，‎ 那么当时，‎ ‎ ，‎ 且，‎ 所以，‎ 所以，‎ 即当时，命题也成立.‎ 根据①②，得对一切，都成立.‎ ‎22.（1）g(x)的定义域为，‎ ‎①当a=0时， 当 ‎②当，此时 ‎ ‎ ‎③当，此时，‎ ‎④当，此时 ‎⑤当a<0时，此时 ‎ ……………7分 ‎（2）由第（1）知 ‎①当时，‎ 故，则a=-2‎ ‎②当，此时 ‎，矛盾 ‎③当，此时 g(x)最大值可能在x=1或x=e处取得，而g(1)=ln1+a-(2a+1)<0‎ 故，则与矛盾，舍去 综上所述：a=-2 …………….12分