数学（文）卷·2019届河北省承德一中高二上学期第三次月考（2017-11） 8页

河北承德第一中学 2017-2018 学年度第一学期第三次月考 高二数学试题（文科） 时间：120 分钟 总分：150 分 出题人： 一、本试卷分第Ⅰ卷（选择题 60 分）和第Ⅱ卷（非选择题 90 分）两部分，满分 150 分。 二、本次考试内容：①必修 2 第四章圆与方程；②选修 1-1 第一章简易逻辑； ③选修 1-1 第二章圆锥曲线与方程；④必修 3 第一章算法初步。 第Ⅰ卷（选择题 60 分） 一、选择题：(共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只 有一项是符合题目要求的) 1.平面内的点 P 到两定点 F1、F2 距离之和为 m（m 为常数且 m>|F1F2|）的点的轨迹 为（ ） A.线段 B.椭圆 C.双曲线 D.抛物线 2.在流程图中分别表示判断框、输入（出）框、处理框的是（ ） A. B. C. D. 3.下列关于四种命题的真假判断正确的是（ ） A.原命题与其逆否命题的真值相同 B.原命题与其逆命题的真值相同 C.原命题与其否命题的真值相同 D.原命题的逆命题与否命题的真值相反 4.点 A(1，2)与圆 C：(x+1)2+(y-2)2=1 的位置关系是（ ） A.圆内 B.圆外 C.圆上 D.不能确定 5.如图所示的程序框图的运行结果是( ) A．2B．2.5C．3.5D．4 A．若“|x|<1”是“x0 B.a>0,b<0 C.a<0,b<0 D.a<0,b>0 8.用更相减损术求 294 和 84 的最大公约数时，需要做减法的次数为( ) A．2B．3C．4D．5 9.已知命题 p：∀x1、x2∈R，(f(x2)－f(x1))(x2－x1)≥0，则¬p 是( ) A．∃x1、x2∈R，(f(x2)－f(x1))(x2－x1)≤0 B．∀x1、x2∈R，(f(x2)－f(x1))(x2－x1)≤0 C．∀x1、x2∈R，(f(x2)－f(x1))(x2－x1)<0 D．∃x1、x2∈R，(f(x2)－f(x1))(x2－x1)<0 10.用秦九韶算法求多项式 f(x)＝12＋35x－8x2＋79x3＋6x4＋5x5＋3x6 在 x＝－4 的值时，v4 的值为( ) A．－57B．220C．－845D．3 392 11.过双曲线 - =1(a>0,b>0)的右顶点 A 作斜率为-1 的直线,该直线与双曲线的 两条渐近线的交点分别为 B,C.若 BCAB 2 1 ,则双曲线的离心率是 ( ) A. 2 B. 3 C. 5 D. 10 12.设抛物线 C:y2=4x的焦点为 F,直线 l 过点 F 且与 C交于 A,B 两点.若|AF|=3|BF|, 则 l 的方程为 ( ) A.y= 3 (x-1)或 y=- 3 (x-1)B.y= (x-1)或 y=- (x-1) C.y=x-1 或 y=-x+1D.y= (x-1)或 y=- (x-1) 第Ⅱ卷（非选择题 90 分） 二、填空题：(共 4 小题,每小题 5 分,共 20 分.请把正确答案填在题中横线上) 13.536(7)=(9) 14.已知两圆相交于两点 A(1,3)，B(m，－1)，两圆圆心都在直线 x－y ＋c＝0 上，则 m＋c 的值是. 15.某程序框图如图所示，该程序运行后输出 S 的结果是. 16.已知点 P 是抛物线 y2=4x 上的动点,点 P 在 y 轴上的射影是 M,点 A(4,6),则|PA|+|PM|的最小值是 . 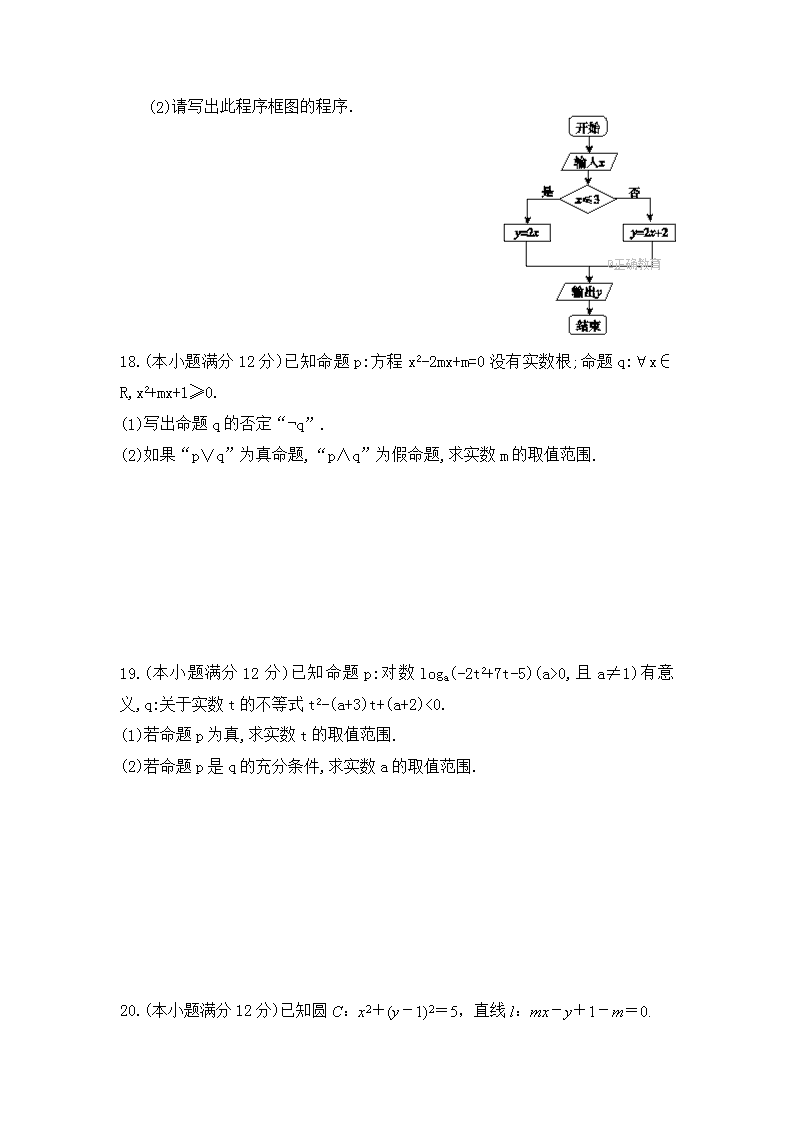三、解答题(共 6 小题,共 70 分.解答时应写出必要的文字说明、证明过程或演算 步骤) 17.(本小题满分 10 分)给出一个算法的程序框图(如图所示)． (1)说明该程序框图的功能； (2)请写出此程序框图的程序． 18.(本小题满分 12 分)已知命题 p:方程 x2-2mx+m=0 没有实数根;命题 q:  x∈ R,x2+mx+1≥0. (1)写出命题 q 的否定“¬q”. (2)如果“p∨q”为真命题,“p∧q”为假命题,求实数 m 的取值范围. 19.(本小题满分12分)已知命题p:对数loga(-2t2+7t-5)(a>0,且a≠1)有意义,q: 关于实数 t 的不等式 t2-(a+3)t+(a+2)<0. (1)若命题 p 为真,求实数 t 的取值范围. (2)若命题 p 是 q 的充分条件,求实数 a 的取值范围. 20.(本小题满分 12 分)已知圆 C：x2＋(y－1)2＝5，直线 l：mx－y＋1－m＝0. (1)求证：对 m∈R，直线 l 与圆 C 总有两个不同的交点； (2)若直线 l 与圆 C 交于 A、B 两点，当|AB|＝ 17时，求 m 的值． 21.(本小题满分 12 分)已知抛物线 y2=-x 与直线 y=k(x+1)相交于 A,B 两点. (1)求证:OA⊥OB. (2)当△OAB 的面积等于 10 时,求 k 的值. 22.(本小题满分 12 分)已知椭圆 C: + =1 过 A(2,0),B(0,1)两点. (1)求椭圆 C 的方程及离心率. (2)设 P 为第三象限内一点且在椭圆 C 上,直线 PA 与 y 轴交于点 M,直线 PB 与 x 轴交于点 N,求证:四边形 ABNM 的面积为定值. 2017-2018 学年度第一学期第三次月考 高二数学试题（文科）参考答案 一、选择题： BCABB CDCDB CA 二、填空题： 13.332 14.3 15. 12 25 16. 153  三、解答题： 17.【解析】（1）该流程图的功能是求函数      3,22 3,2 xx xxy 的函数值； （2）该流程图的程序为： 18.【解析】(1)¬q:x0∈R, +mx0+1<0. (2)若方程 x2-2mx+m=0 没有实数根,则Δ=4m2-4m<0,解得 00,解得 1