【数学】2020届一轮复习人教版（理）第3章第7讲解三角形应用举例学案 11页

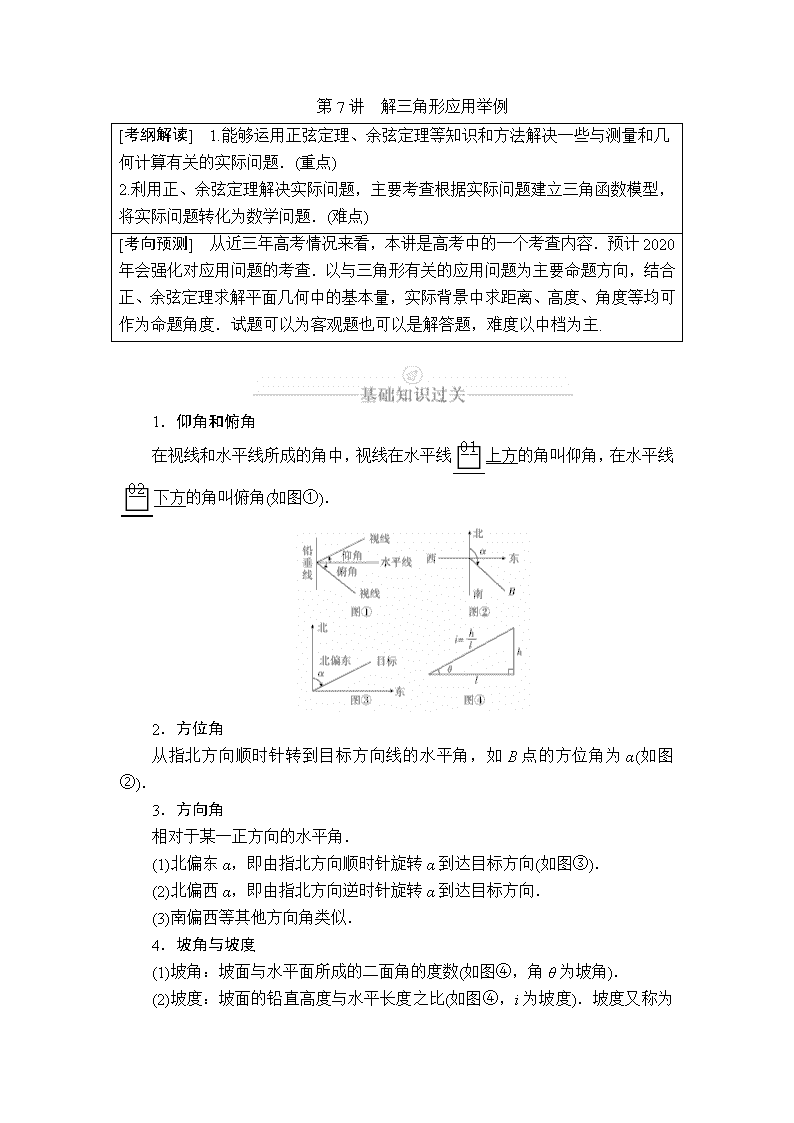
第7讲　解三角形应用举例 ‎[考纲解读]　1.能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题．(重点)‎ ‎2.利用正、余弦定理解决实际问题，主要考查根据实际问题建立三角函数模型，将实际问题转化为数学问题．(难点)‎ ‎[考向预测]　从近三年高考情况来看，本讲是高考中的一个考查内容．预计2020年会强化对应用问题的考查．以与三角形有关的应用问题为主要命题方向，结合正、余弦定理求解平面几何中的基本量，实际背景中求距离、高度、角度等均可作为命题角度．试题可以为客观题也可以是解答题，难度以中档为主.‎ ‎1．仰角和俯角 在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫俯角(如图①)．‎ ‎2．方位角 从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α(如图②)．‎ ‎3．方向角 相对于某一正方向的水平角．‎ ‎(1)北偏东α，即由指北方向顺时针旋转α到达目标方向(如图③)．‎ ‎(2)北偏西α，即由指北方向逆时针旋转α到达目标方向．‎ ‎(3)南偏西等其他方向角类似．‎ ‎4．坡角与坡度 ‎(1)坡角：坡面与水平面所成的二面角的度数(如图④，角θ为坡角)．‎ ‎(2)坡度：坡面的铅直高度与水平长度之比(如图④，i 为坡度)．坡度又称为坡比．‎ ‎1．概念辨析 ‎(1)东北方向就是北偏东45°的方向．(　　)‎ ‎(2)从A处望B处的仰角为α，从B处望A处的俯角为β，则α，β的关系为α＋β＝180°.(　　)‎ ‎(3)方位角与方向角其实质是一样的，均是确定观察点与目标点之间的位置关系．(　　)‎ ‎(4)方位角大小的范围是[0,2π)，方向角大小的范围一般是.(　　)‎ 答案　(1)√　(2)×　(3)√　(4)√‎ ‎　 　　　　　　　　　　　　　　　　　　‎ ‎2．小题热身 ‎(1)已知A，B两地间的距离为10 km，B，C两地间的距离为20 km，现测得∠ABC＝120°，则A，C两地间的距离为(　　)‎ A．10 km B．10 km C．10 km D．10 km 答案　D 解析　由余弦定理可得，AC2＝AB2＋CB2－2AB·CB·cos120°＝102＋202－2×10×20×＝700.‎ ‎∴AC＝10(km)．‎ ‎(2)如图，为测一树的高度，在地面上选取A，B两点，在A，B两点分别测得树顶的仰角为30°，45°，且A，B两点之间的距离为10 m，则树的高度h为(　　)‎ A．(5＋5) m B．(30＋15) m C．(15＋30) m D．(15＋3) m 答案　A 解析　在△PAB中，由正弦定理得 ＝，所以PB＝＝，‎ 所以h＝PBsin45°＝＝＝(5＋5) m.‎ ‎(3)如图，从无人机A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时无人机的高度是46 m，则河流的宽度BC约等于________ m．(用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，≈1.73)‎ 答案　60‎ 解析　由图可知，AB＝，在△ABC中，由正弦定理可知＝，所以BC＝＝≈＝60(m)．‎ ‎(4)在某点B处测得建筑物AE的顶端A的仰角为θ，沿BE方向前进30 m，至点C处测得顶端A的仰角为2θ，再继续前进10 m至D点，测得顶端A的仰角为4θ，则θ的大小为________．‎ 答案　15°‎ 解析　在△ACD中，AC＝BC＝30，AD＝CD＝10，‎ ‎∠ADC＝180°－4θ，‎ 由正弦定理得＝，‎ 所以＝，cos2θ＝，‎ 所以2θ＝30°，θ＝15°.‎ 题型 　测量距离问题 ‎1．一艘船以每小时15 km的速度向东航行，船在A处看到一个灯塔M在北偏东60°方向，行驶4 h后，船到达B处，看到这个灯塔在北偏东15°方向，这时船与灯塔的距离为(　　)‎ A．15 km B．30 km C．45 km D．60 km 答案　B 解析　作出示意图如图所示，依题意有AB＝15×4＝60，∠DAC＝60°，∠CBM＝15°，‎ ‎∴∠MAB＝30°，∠AMB＝45°.‎ 在△AMB中，由正弦定理，得＝，‎ 解得BM＝30.‎ ‎2．如图，A，B两点在河的同侧，且A，B两点均不可到达，要测出A，B的距离，测量者可以在河岸边选定两点C，D，测得CD＝a，同时在C，D两点分别测得∠BCA＝α，∠ACD＝β，∠CDB＝γ，∠BDA＝δ.在△ADC和△BDC中，由正弦定理分别计算出AC和BC，再在△ABC中，应用余弦定理计算出AB.‎ 若测得CD＝ km，∠ADB＝∠CDB＝30°，∠ACD＝60°，∠ACB＝45°，则A，B两点间的距离为________km.‎ 答案　 解析　∵∠ADC＝∠ADB＋∠CDB＝60°，∠ACD＝60°，‎ ‎∴∠DAC＝60°，∴AC＝DC＝(km)．‎ 在△BCD中，∠DBC＝45°，由正弦定理，得 BC＝·sin∠BDC＝·sin30°＝.‎ 在△ABC中，由余弦定理，得 AB2＝AC2＋BC2－2AC·BC·cos45°‎ ‎＝＋－2×××＝.‎ ‎∴AB＝(km)．∴A，B两点间的距离为 km.‎ ‎(1)测量距离问题，无论题型如何变化，即两点的情况如何变化，实质都是要求这两点间的距离，无非就是两点所在三角形及其构成元素的所知情况不同而已，恰当地画出(找出)适合解决问题的三角形是解题的基础，将已知线段长度和角度转化为要解的三角形的边长和角是解题的关键．‎ ‎(2)求距离问题的两个策略 ‎①选定或确定要创建的三角形，首先确定所求量所在的三角形，若其他量已知则直接求解；若有未知量，则把未知量放在另一确定三角形中求解．‎ ‎②确定用正弦定理还是余弦定理，如果都可用，就选择更便于计算的定理．　 　　　　　　　　　　　　　　　　　　‎ ‎(2018·广州模拟)如图，在海岸线上相距2千米的A，C两地分别测得小岛B在A的北偏西α方向，在C的北偏西－α方向，且cosα＝，则B，C之间的距离是(　　)‎ A．30千米 B．30千米 C．12千米 D．12千米 答案　D 解析　由题意得AC＝2，‎ sinA＝sin＝cosα＝，‎ sinB＝sin＝cos2α＝2cos2α－1＝，‎ 在△ABC中，由正弦定理得 BC＝＝＝12，‎ 则C与B的距离是12千米．‎ 题型 　测量高度问题 ‎1．(2018·山西五校联考)飞机的航线和山顶在同一个铅垂平面内，已知飞机的高度为海拔15000 m，速度为1000 km/h，飞行员先看到山顶的俯角为15°，经过108 s后又看到山顶的俯角为75°，则山顶的海拔高度为________m(取＝1.732)．‎ 答案　6340‎ 解析　∵108 s＝0.03 h，‎ ‎∴AB＝1000×0.03＝30 km.‎ ‎∵∠C＝75°－15°＝60°，‎ ‎∴＝，∴BC＝.‎ ‎∴C到AB边的距离为h＝BCsin75°＝20sin15°sin75°＝10sin30°＝5＝5×1.732＝8.66 km.‎ ‎∴山顶的海拔高度为(15－8.66) km＝6340 m.‎ ‎2．(2018·福州质检)如图，小明同学在山顶A处观测到一辆汽车在一条水平的公路上沿直线匀速行驶，小明在A处测得公路上B，C两点的俯角分别为30°，45°，且∠BAC＝135°.若山高AD＝100 m，汽车从B点到C点历时14 s，则这辆汽车的速度约为________m/s(精确到0.1)．‎ 参考数据：≈1.414，≈2.236.‎ 答案　22.6‎ 解析　因为小明在A处测得公路上B，C两点的俯角分别为30°，45°，所以∠BAD＝60°，∠CAD＝45°.‎ 设这辆汽车的速度为v m/s，则BC＝14v.‎ 在Rt△ADB中，AB＝＝＝200.‎ 在Rt△ADC中，AC＝＝＝100.‎ 在△ABC中，由余弦定理，‎ 得BC2＝AC2＋AB2－2AC·AB·cos∠BAC，‎ 所以(14v)2＝(100)2＋2002－2×100×200×cos135°，所以v＝≈22.6，所以这辆汽车的速度约为22.6 m/s.‎ 条件探究　将举例说明2中的条件改为“‎ 如图，一辆汽车在一条水平的公路上向正西行驶，到B处时测得公路北侧一山顶A在西偏北30°的方向上，行驶600 m后到达C处，测得此山顶在西偏北75°的方向上，仰角为30°”，求此山的高度AD.‎ 解　由题意，在△BCD中，∠CBD＝30°，‎ ‎∠BCD＝180°－75°＝105°，故∠BDC＝45°.‎ 又BC＝600 m，故由正弦定理得＝，‎ 解得CD＝300 m.‎ 在Rt△ACD中，AD＝CD·tan30°＝300× ‎＝100(m)．‎ 求解高度问题的注意事项 ‎(1)理解仰角、俯角(它是在铅垂面上所成的角)、方向(位)角(它是在水平面上所成的角)等的定义．‎ ‎(2)在实际问题中，可能会遇到空间与平面(地面)同时研究的问题，这时最好画两个图形，一个空间图形，一个平面图形，这样处理起来既清楚又不容易搞错．‎ ‎(3)注意山或塔垂直于地面或海平面，把空间问题转化为平面问题．　 　　　　　　　　　　　　　　　　　　‎ ‎1．如图，在离地面高400 m的热气球上，观测到山顶C处的仰角为15°，山脚A处的俯角为45°，已知∠BAC＝60°，则山的高度BC为(　　)‎ A．700 m B．640 m C．600 m D．560 m 答案　C 解析　在Rt△AMD中，AM＝＝＝400，在△MAC中，∠AMC＝45°＋15°＝60°，∠MAC＝180°－45°－60°＝75°，∠MCA＝180°－∠AMC－∠MAC＝45°，由正弦定理得AC＝＝＝400.在Rt△ABC中，BC＝ACsin∠BAC＝400×＝600(m)．‎ ‎2．如图所示，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN＝60°，C点的仰角∠CAB＝45°以及∠MAC＝75°；从C点测得∠MCA＝60°.已知山高BC＝100 m，则山高MN＝________ m.‎ 答案　150‎ 解析　在△ABC中，AC＝100，在△MAC中，＝，解得MA＝100，在△MNA中，＝sin60°＝，故MN＝150，即山高MN为150 m.‎ 题型 　测量角度问题 在一次海上联合作战演习中，红方一艘侦察艇发现在北偏东45°方向，相距12 n mile的水面上，有蓝方一艘小艇正以每小时10 n mile的速度沿南偏东75°方向前进，若红方侦察艇以每小时14 n mile的速度沿北偏东45°＋α方向拦截蓝方的小艇．若要在最短的时间内拦截住，求红方侦察艇所需的时间和角α的正弦值．‎ 解　如图，设红方侦察艇经过x小时后在C处拦截住蓝方的小艇，则AC ‎＝14x，BC＝10x，∠ABC＝120°.‎ 根据余弦定理得 ‎(14x)2＝122＋(10x)2－240xcos120°，‎ 解得x＝2.‎ 故AC＝28，BC＝20.‎ 根据正弦定理得＝，‎ 解得sinα＝＝.‎ 所以红方侦察艇所需的时间为2小时，角α的正弦值为.‎ 解决测量角度问题的注意事项 ‎(1)测量角度时，首先应明确方位角及方向角的含义．‎ ‎(2)求角的大小时，先在三角形中求出其正弦或余弦值．‎ ‎(3)在解应用题时，要根据题意正确画出示意图，通过这一步可将实际问题转化为可用数学方法解决的问题，解题中也要注意体会正、余弦定理“联袂”使用的优点．　 　　　　　　　　　　　　　　　　　　‎ 如图所示，位于A处的信息中心获悉：在A处的正东方向相距40海里的B处有一艘渔船遇险，在原地等待营救．信息中心立即把消息告知在A处的南偏西30°、相距20海里的C处的乙船，现乙船朝北偏东θ的方向沿直线CB前往B处救援，则cosθ等于(　　)‎ A. B. C. D. 答案　B 解析　在△ABC中，AB＝40，AC＝20，∠BAC＝120°，由余弦定理得BC2＝AB2＋AC2－2AB·AC·cos120°＝2800，所以BC＝20.由正弦定理得sin∠ACB＝·sin∠BAC＝.由∠BAC＝120°知∠ACB为锐角，故cos∠ACB＝，故cosθ＝cos(∠ACB＋30°)＝cos∠ACB·cos30°－sin∠ACB·sin30°＝.‎