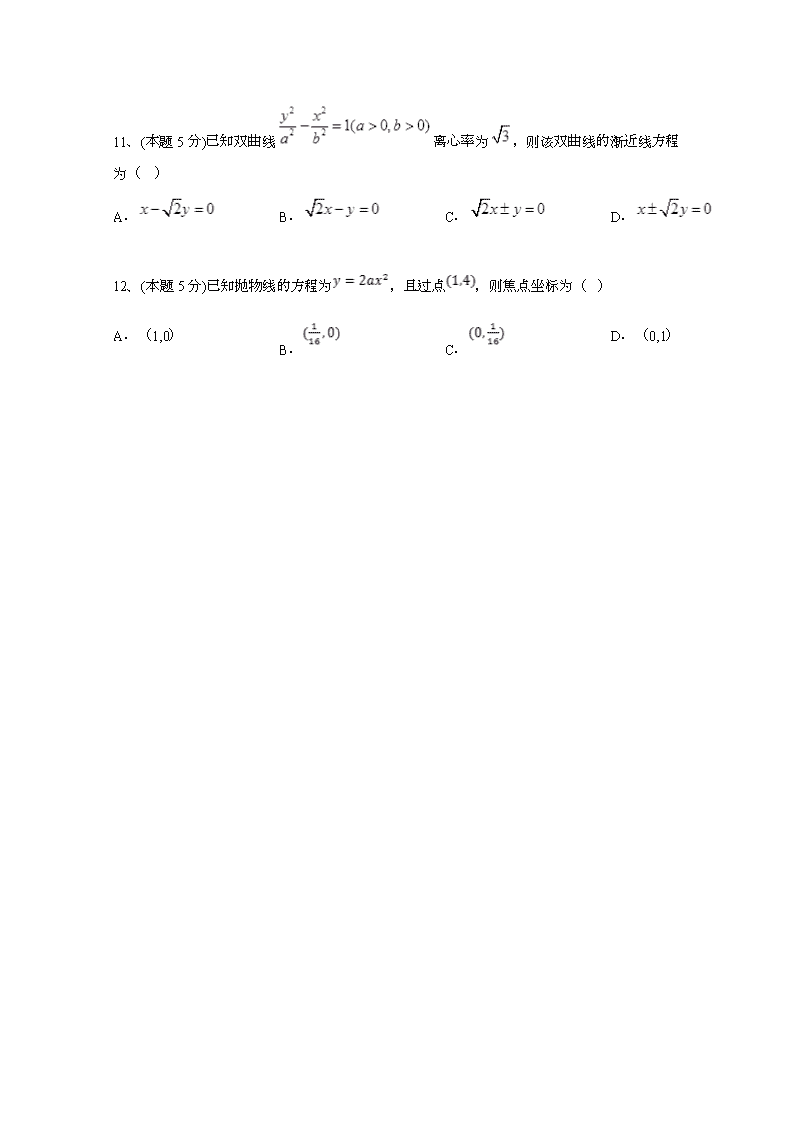2017-2018学年云南省昆明市黄冈实验学校高二下学期期中考试数学（理）试题 Word版 16页

绝密★启用前 昆明黄冈实验学校2017-2018学年下学期期中考试卷 高二年级数学（理科）‎ 注意事项．‎ ‎1．答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡上 第I卷（选择题）‎ 一、选择题（本题共12题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1、(本题5分)函数y＝的导数是                   (　　)‎ A．‎ B．‎ C．‎ D．‎ ‎2、(本题5分)垂直于直线，且与曲线相切的直线方程是（  ）‎ A．‎ B．‎ C．‎ D．‎ ‎3、(本题5分)已知函数，且，则实数的值为（  ）‎ A．‎ B．‎ C．‎ D．‎ ‎4、(本题5分)已知为虚数单位，复数满足，则的共轭复数 (   )‎ A．‎ B．‎ C．‎ D．‎ ‎5、(本题5分)复数（为虚数单位）在复平面内对应的点位于（）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎6、(本题5分)若复数Z满足（为虚数单位），则Z的共轭复数为(   )‎ A．‎ B．‎ C．‎ D．‎ ‎7、(本题5分)已知的导函数，则 A．‎ B．‎ C．‎ D．‎ ‎8、(本题5分)一名老师和四名学生站成一排照相，学生请老师站在正中间，则不同的站法为 A．4种 B．12种 C．24种 D．120种 ‎9、(本题5分)设集合，则（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎10、(本题5分)已知向量，若（）与互相垂直，则的值为 A．‎ B．‎ C．‎ D．‎ ‎11、(本题5分)已知双曲线离心率为，则该双曲线的渐近线方程为（    ）‎ A．‎ B．‎ C．‎ D．‎ ‎12、(本题5分)已知抛物线的方程为，且过点，则焦点坐标为（   ）‎ A．（1,0）‎ B．‎ C．‎ D．（0,1）‎ ‎第II卷（非选择题）‎ 二、填空题（本题共4小题，每小题5分，共20分）‎ ‎13、(本题5分)曲线在点处的切线方程为__________．‎ ‎14、(本题5分)定积分的值等于________．‎ ‎15、(本题5分)已知复数，其中是虚数单位，则复数在复平面上对应的点位 于第______象限．‎ ‎16、(本题5分)已知复数满足，则复数_______．‎ 三、解答题（解答应写上文字说明，证明过程或演算步骤。第17题10分，其余5题各12分，共70分）‎ ‎17、(本题10分)已知集合，. 求，，‎ 18、 ‎(本题12分)已知函数在处有极值. （1）求，的值； （2）判断函数的单调性并求出单调区间.‎ 19、 ‎(本题12分)在锐角中，内角的对边分别是，且. （1）求； （2）若，的面积为3，求的值.‎ ‎20、(本题12分)求椭圆 16x2+25y2=400的长轴和短轴的长，离心率，焦点和顶点坐标．‎ ‎21、(本题12分)（1）设等差数列满足，前3项和，求数列的通项公式； （2）数列是等比数列，，，求其通项公式．‎ ‎22、(本题12分)已知. （1）求函数的定义域； （2）判断函数的奇偶性，并加以说明； （3）求的值.‎ 绝密★启用前 ‎ ‎ 昆明黄冈实验学校高二期中检测试卷答案（理科）‎ ‎ ‎ ‎ ‎ 注意事项．‎ ‎1．答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡上 ‎ ‎ 第I卷（选择题）‎ ‎ ‎ ‎ ‎ 一、选择题（本题共12题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎ ‎ ‎1、(本题5分)函数y＝的导数是 ( )‎ A． B． C． D． ‎ ‎【答案】C【解析】由求导公式可得：，故选C.‎ ‎2、(本题5分)垂直于直线，且与曲线相切的直线方程是（ ）‎ A． B． C． D．‎ ‎ ‎ ‎【答案】A ‎【解析】，设切点为，则，解得，从而切点为，切线方程为，整理得．选A．‎ ‎3、(本题5分)已知函数，且，则实数的值为（ ）‎ A． B． C． D． ‎ ‎ ‎ ‎【答案】A ‎【解析】由题意可得，，选A.‎ ‎4、(本题5分)已知为虚数单位，复数满足，则的共轭复数 ( )‎ A． B． C． D． ‎ ‎ ‎ ‎【答案】A ‎【解析】由，得，故选A.‎ ‎5、(本题5分)复数（为虚数单位）在复平面内对应的点位于（）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎ ‎ ‎ ‎【答案】D ‎【解析】 对应的点为 故选D ‎6、(本题5分)若复数Z满足（为虚数单位），则Z的共轭复数为( )‎ A． B． C． D． ‎ ‎ ‎ ‎【答案】A ‎【解析】 =,,选A.‎ ‎7、(本题5分)已知的导函数，则 A． B． C． D． ‎ ‎ ‎ ‎【答案】A ‎【解析】，选A.‎ ‎8、(本题5分)一名老师和四名学生站成一排照相，学生请老师站在正中间，则不同的站法为 A．4种 B．12种 C．24种 D．120种 ‎ ‎ ‎ ‎【答案】C ‎【解析】一名老师和四名学生站成一排照相，老师站在正中间，则不同的站法为种，选C.‎ ‎9、(本题5分)设集合，则（ ）‎ A． B． C． D． []‎ ‎ ‎ ‎【答案】D ‎【解析】集合或，则，故选D.‎ ‎10、(本题5分)已知向量，若（）与互相垂直，则的值为 A． B． C． D． ‎ ‎ ‎ ‎【答案】D ‎【解析】，因为（）与互相垂直，则，选D.‎ ‎11、(本题5分)已知双曲线离心率为，则该双曲线的渐近线方程为（ ）‎ A． B． C． D． ‎ ‎ ‎ ‎【答案】D ‎【解析】，则，双曲线的渐近线方程为，选D.‎ ‎12、(本题5分)已知抛物线的方程为，且过点，则焦点坐标为（ ）‎ A．（1,0） B． C． D．（0,1） ‎ ‎ ‎ ‎【答案】C ‎【解析】根据抛物线标准方程得到 ， ，焦点坐标为 ，代入可得焦点坐标为 ，将点代入抛物线方程得到a=2,故最终得到焦点坐标为. 故答案选C.‎ 第II卷（非选择题）‎ ‎ ‎ ‎ ‎ 二、填空题（本题共4小题，每小题5分，共20分）‎ ‎ ‎ ‎13、(本题5分)曲线在点处的切线方程为__________．‎ ‎ ‎ ‎【答案】‎ ‎【解析】曲线在点处的斜率为： 根据点斜式写出直线方程为：. 故答案为：.‎ ‎14、(本题5分)定积分的值等于________．‎ ‎ ‎ ‎【答案】0‎ ‎【解析】，故答案为.‎ ‎15、(本题5分)已知复数，其中是虚数单位，则复数在复平面上对应的点位 于第______象限．‎ ‎ ‎ ‎【答案】一 ‎【解析】复数，复数在复平面上对应的点位于第一象限， 故答案为一．‎ ‎16、(本题5分)已知复数满足，则复数_______．‎ ‎ ‎ ‎【答案】‎ ‎【解析】，，故答案为.‎ ‎ ‎ 三、解答题（解答应写上文字说明，证明过程或演算步骤。第17题10分，其余5题各12分，共70分）‎ ‎ ‎ ‎17、(本题10分)已知集合，. 求，，‎ ‎ ‎ ‎【答案】； ；‎ ‎【解析】试题分析：对于连续区间上的集合交、并、补运算，我们常借助于数轴，特别要注意实心点，空心点的标注，也就是注意端点问题。 试题解析：； ‎ ‎18、(本题12分)已知函数在处有极值. （1）求，的值； （2）判断函数的单调性并求出单调区间.‎ ‎ ‎ ‎【答案】(1) a＝，b＝－1 (2)函数的单调减区间是（0,1），单调增区间是（1，＋∞）‎ ‎【解析】试题分析：（1）因为在处有极值，故，从而.（2）求得，则当时，‎ ‎，因此增区间为；当 时，有，因此减区间为. 解析：（1）∵ ，又在处有极值，∴ 即解得. （2）由（1）可知，其定义域是，，由，得；由，得. 所以函数的单调减区间是，单调增区间是． ‎ ‎19、(本题12分)在锐角中，内角的对边分别是，且. （1）求； （2）若，的面积为3，求的值.‎ ‎ ‎ ‎【答案】（1）；（2）15.‎ ‎【解析】试题分析：（1）由条件利用二倍角公式求得，可得A的值． （2）由条件利用△ABC的面积为3求得bc=12，再利用余弦定理求得b-c的值． 试题解析： （1）因为， 所以，即. 又因为为锐角三角形，所以，所以 ‎. （2）因为，所以. 又因为，所以，所以. 故 .‎ ‎20、(本题12分)求椭圆 16x2+25y2=400的长轴和短轴的长，离心率，焦点和顶点坐标．‎ ‎ ‎ ‎【答案】详见解析 ‎【解析】试题分析：有关椭圆的简单几何性质问题，首先把椭圆方程化为标准方程，先得出，求出，根据，求出，然后写出长轴，短轴，计算离心率，根据焦点的位置写出焦点的坐标，最后在写出四个顶点的坐标.一要注意焦点在那个轴上，二要注意和和的区别. 试题解析： 由题知 得a=5，b=4，c=3， 所以长轴长2a=10，短轴长：2b=8 离心率：e=，焦点F1（3，0）F2（﹣3，0 ）， 顶点坐标 （5，0）、（﹣5，0）、（0，4）、（0，﹣4）．‎ ‎21、(本题12分)（1）设等差数列满足，前3项和，求数列的通项公式； （2）数列是等比数列，，，求其通项公式．‎ ‎ ‎ ‎【答案】（1）; （2）;‎ ‎【解析】试题分析：（1）根据等差数列的前 项和公式结合已知条件求可得 ，再根据等差数列的通项公式可得；（2）根据等比数列的通项公式结合已知条件可得，求得或；再根据等比数列的通项公式得. 试题解析： （1） （2） 或 ‎ ‎22、(本题12分)已知. （1）求函数的定义域； （2）判断函数的奇偶性，并加以说明； （3）求的值.‎ ‎ ‎ ‎【答案】(1) (2) 偶函数 (3) ‎ ‎【解析】试题分析：（1）根据定义域的要求解出定义域即可；（2）奇偶性的证明首先定义域对称，再求解，得，所以为偶函数；（3）按照对数计算公式求解 ‎。 试题解析： （1）由得 所以函数的域为 （2）因为函数的域为 又 所以函数为偶函数 （3） ‎ ‎ ‎