【数学】2018届一轮复习人教A版导数与函数的单调性学案 8页

第 2 讲　导数与函数的单调性 最新考纲　了解函数的单调性与导数的关系；能利用导数研究函数的单调性，会求函数的单 调区间(其中多项式函数不超过三次). 知 识 梳 理 1.函数的单调性与导数的关系 已知函数 f(x)在某个区间内可导， (1)如果 f′(x)＞0，那么函数 y＝f(x)在这个区间内单调递增； (2)如果 f′(x)＜0，那么函数 y＝f(x)在这个区间内单调递减. 2.利用导数求函数单调区间的基本步骤是： (1)确定函数 f(x)的定义域； (2)求导数 f′(x)； (3)由 f′(x)＞0(或＜0)解出相应的 x 的取值范围.当 f′(x)＞0 时，f(x)在相应的区间内是 单调递增函数；当 f′(x)＜0 时，f(x)在相应的区间内是单调递减函数. 一般需要通过列表，写出函数的单调区间. 3.已知单调性求解参数范围的步骤为： (1)对含参数的函数 f(x)求导，得到 f′(x)； (2)若函数 f(x)在[a，b]上单调递增，则 f′(x)≥0 恒成立；若函数 f(x)在[a，b]上单调递 减，则 f′(x)≤0 恒成立，得到关于参数的不等式，解出参数范围； (3)验证参数范围中取等号时，是否恒有 f′(x)＝0.若 f′(x)＝0 恒成立，则函数 f(x)在(a， b)上为常数函数，舍去此参数值. 诊 断 自 测 1.判断正误(在括号内打“√”或“×”) (1)若函数 f(x)在(a，b)内单调递增，那么一定有 f′(x)>0.(　　) (2)如果函数 f(x)在某个区间内恒有 f′(x)＝0，则 f(x)在此区间内没有单调性.(　　) (3)f′(x)>0 是 f(x)为增函数的充要条件.(　　) 解析　(1)f(x)在(a，b)内单调递增，则有 f′(x)≥0. (2)f′(x)>0 是 f(x)为增函数的充分不必要条件. 答案　(1)×　(2)√　(3)× 2.函数 f(x)＝ex－x 的单调递增区间是(　　) A.(－∞，1] B.[1，＋∞) C.(－∞，0] D.(0，＋∞) 解析　令 f′(x)＝ex－1>0 得 x>0，所以 f(x)的递增区间为(0，＋∞). 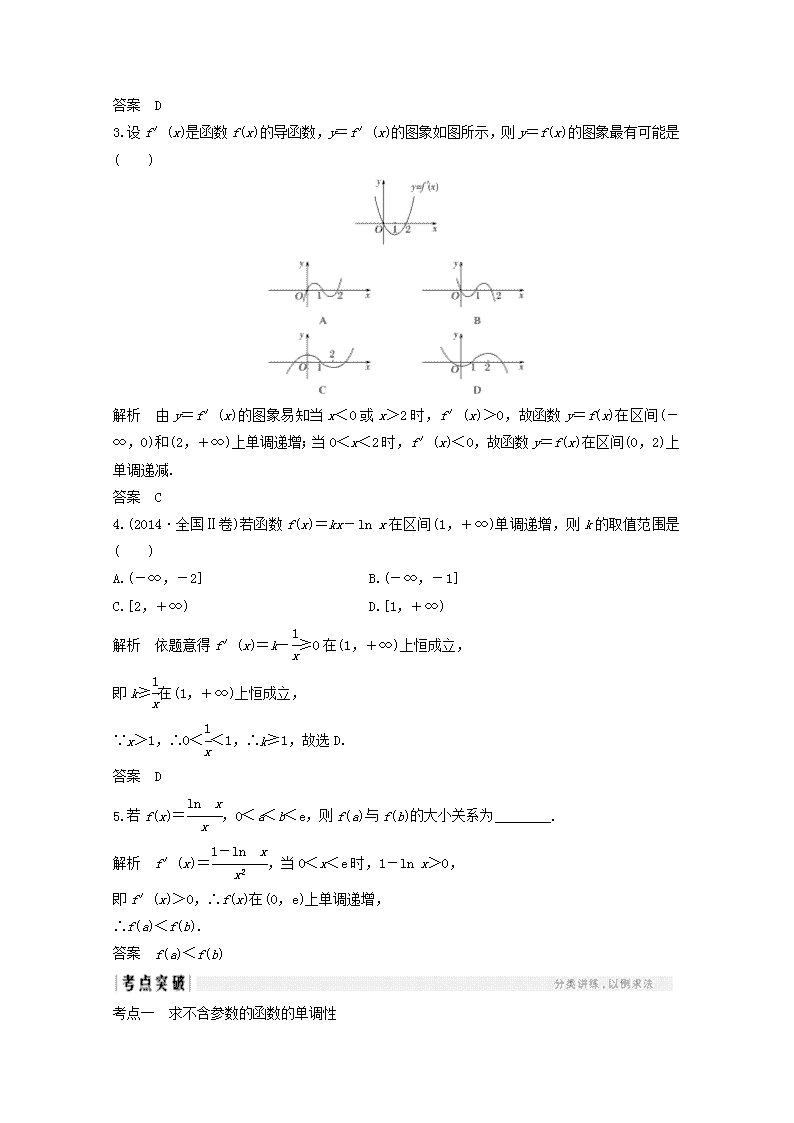答案　D 3.设 f′(x)是函数 f(x)的导函数，y＝f′(x)的图象如图所示，则 y＝f(x)的图象最有可能是 (　　) 解析　由 y＝f′(x)的图象易知当 x＜0 或 x＞2 时，f′(x)＞0，故函数 y＝f(x)在区间(－ ∞，0)和(2，＋∞)上单调递增；当 0＜x＜2 时，f′(x)＜0，故函数 y＝f(x)在区间(0，2)上 单调递减. 答案　C 4.(2014·全国Ⅱ卷)若函数 f(x)＝kx－ln x 在区间(1，＋∞)单调递增，则 k 的取值范围是 (　　) A.(－∞，－2] B.(－∞，－1] C.[2，＋∞) D.[1，＋∞) 解析　依题意得 f′(x)＝k－ 1 x≥0 在(1，＋∞)上恒成立， 即 k≥ 1 x在(1，＋∞)上恒成立， ∵x＞1，∴0＜ 1 x＜1，∴k≥1，故选 D. 答案　D 5.若 f(x)＝ ln x x ，0＜a＜b＜e，则 f(a)与 f(b)的大小关系为________. 解析　f′(x)＝ 1－ln x x2 ，当 0＜x＜e 时，1－ln x＞0， 即 f′(x)＞0，∴f(x)在(0，e)上单调递增， ∴f(a)＜f(b). 答案　f(a)＜f(b) 考点一　求不含参数的函数的单调性 【例 1】 已知函数 f(x)＝ax3＋x2(a∈R)在 x＝－ 4 3处取得极值. (1)确定 a 的值； (2)若 g(x)＝f(x)ex，讨论 g(x)的单调性. 解　(1)对 f(x)求导得 f′(x)＝3ax2＋2x， 因为 f(x)在 x＝－ 4 3处取得极值，所以 f′(－ 4 3 )＝0， 所以 3a· 16 9 ＋2·(－ 4 3 )＝ 16a 3 － 8 3＝0，解得 a＝ 1 2. (2)由(1)得 g(x)＝(1 2x3＋x2)ex， 故 g′(x)＝(3 2x2＋2x)ex＋(1 2x3＋x2)ex ＝(1 2x3＋ 5 2x2＋2x)ex ＝ 1 2x(x＋1)(x＋4)ex. 令 g′(x)＝0， 解得 x＝0，x＝－1 或 x＝－4. 当 x<－4 时，g′(x)<0，故 g(x)为减函数； 当－40，故 g(x)为增函数； 当－10 时，g′(x)>0，故 g(x)为增函数. 综上知，g(x)在(－∞，－4)和(－1，0)内为减函数，在(－4，－1)和(0，＋∞)内为增函数. 规律方法　确定函数单调区间的步骤： (1)确定函数 f(x)的定义域； (2)求 f′(x)； (3)解不等式 f′(x)>0，解集在定义域内的部分为单调递增区间； (4)解不等式 f′(x)<0，解集在定义域内的部分为单调递减区间. 【训练 1】 函数 y＝ 1 2x2－ln x 的单调递减区间为(　　) A.(－1，1] B.(0，1] C.[1，＋∞) D.(0，＋∞) 解析　y＝ 1 2x2－ln x，y′＝x－ 1 x＝ x2－1 x ＝ （x－1）（x＋1） x (x>0).令 y′≤0，得 00，此时 f′(x)<0，函数 f(x)单调递减； 当 x∈(1，＋∞)时，g(x)<0， 此时 f′(x)>0，函数 f(x)单调递增； (ⅱ)当 a≠0 时，由 g(x)＝0， 即 ax2－x＋1－a＝0， 解得 x1＝1，x2＝ 1 a－1. ①当 a＝ 1 2时，x1＝x2，g(x)≥0 恒成立，此时 f′(x)≤0，等号只在 x＝1 时取得，所以函数 f(x) 在(0，＋∞)上单调递减； ②当 01>0， x∈(0，1)时，g(x)>0，此时 f′(x)<0，函数 f(x)单调递减； x∈(1， 1 a－1)时，g(x)<0， 此时 f′(x)>0，函数 f(x)单调递增； x∈(1 a－1，＋∞)时，g(x)>0， 此时 f′(x)<0，函数 f(x)单调递减. ③当 a<0 时，由于 1 a－1<0， 当 x∈(0，1)时，g(x)>0， 此时 f′(x)<0，f(x)单调递减； x∈(1，＋∞)时，g(x)<0，此时 f′(x)>0，函数 f(x)单调递增. 综上所述： 当 a≤0 时，函数 f(x)在(0，1)上单调递减，在(1，＋∞)上单调递增； 当 a＝ 1 2时，函数 f(x)在(0，＋∞)上单调递减； 当 0 1 x2－ 2 x有解. 设 G(x)＝ 1 x2－ 2 x，所以只要 a>G(x)min 即可. 而 G(x)＝(1 x－1 ) 2 －1，所以 G(x)min＝－1. 所以 a>－1. (2)由 h(x)在[1，4]上单调递减得， 当 x∈[1，4]时，h′(x)＝ 1 x－ax－2≤0 恒成立，③ 即 a≥ 1 x2－ 2 x恒成立.设 G(x)＝ 1 x2－ 2 x， 所以 a≥G(x)max，而 G(x)＝(1 x－1 ) 2 －1， 因为 x∈[1，4]，所以 1 x∈[1 4，1 ]， 所以 G(x)max＝－ 7 16(此时 x＝4)，所以 a≥－ 7 16. 规律方法　利用单调性求参数的两类热点问题的处理方法 (1)函数 f(x)在区间 D 上存在递增(减)区间. 方法一：转化为“f′(x)>0(<0)在区间 D 上有解”； 方法二：转化为“存在区间 D 的一个子区间使 f′(x)>0(<0)成立”. (2)函数 f(x)在区间 D 上递增(减). 方法一：转化为“f′(x)≥0(≤0)在区间 D 上恒成立”问题； 方法二：转化为“区间 D 是函数 f(x)的单调递增(减)区间的子集”. 易错警示　对于①：处理函数单调性问题时，应先求函数的定义域； 对于②：h(x)在(0，＋∞)上存在递减区间，应等价于 h′(x)<0 在(0，＋∞)上有解，易误认 为“等价于 h′(x)≤0 在(0，＋∞)上有解”，多带一个“＝”之所以不正确，是因为“h′(x) ≤0 在(0，＋∞)上有解即为 h′(x)<0 在(0，＋∞)上有解，或 h′(x)＝0 在(0，＋∞)上有 解”，后者显然不正确； 对于③：h(x)在[1，4]上单调递减，应等价于 h′(x)≤0 在[1，4]上恒成立，易误认为“等 价于 h′(x)<0 在[1，4]上恒成立”. 【训练 3】 (1)函数 f(x)＝ 1 3x3－ a 2x2＋2x＋1 的递减区间为(－2，－1)，则实数 a 的值为 ________. (2)(2017·舟山模拟)若 f(x)＝－ 1 2x2＋bln(x＋2)在[－1，＋∞)上是减函数，则实数 b 的取 值范围是________. 解析　(1)f′(x)＝x2－ax＋2，由已知得－2，－1 是 f′(x)的两个零点， 所以有{f′（－2）＝4＋2a＋2＝0， f′（－1）＝1＋a＋2＝0， 解得 a＝－3. (2)由已知得 f′(x)＝－x＋ b x＋2≤0 在[－1，＋∞)上恒成立， ∴b≤(x＋1)2－1 在[－1，＋∞)上恒成立，∴b≤－1. 答案　(1)－3　(2)(－∞，－1] [思想方法] 1.分类讨论思想.解含有参数的单调性问题时，应注意合理分类讨论，分类要做到不重不漏. 2.转化思想.求函数单调性问题转化为解导函数的不等式问题；函数存在单调区间问题转化为 导函数的不等式有解问题，即能成立问题；函数在区间上单调问题转化为导函数的不等式在 区间上恒成立问题. [易错防范] 1.解函数单调性有关问题时务必先求定义域，不能忽视定义域. 2.讨论含参数函数的单调性时易漏某些分类，如本节训练 2 中，易漏 a＝0，a＝ 1 2的情况. 3.函数 f(x)在区间 D 上递增(减)⇔f′(x)≥0(≤0)在区间 D 上恒成立，此处易漏“＝”. 4.函数 f(x)在区间 D 上存在递增(减)区间⇔f′(x)>0(<0)在 D 上有解，此处易误多加“＝”.