广东省湛江市普通高中毕业班2018届高考数学一轮复习模拟试题 10 8页

全*品*高*考*网， 用后离不了！一轮复习数学模拟试题10‎ 满分150分.时间120分钟.‎ 一.填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.‎ ‎1. 不等式的解为 . ‎ ‎（第4题图）‎ ‎2. 函数的最小正周期 . ‎ ‎3. 若集合，集合,,,,，则 . ‎ ‎4.如图，正方体中，直线与平面 所成的角的大小为 （结果用反三角函数值表示）. ‎ ‎5. 若函数的图像经过点，则 .‎ ‎6. 若等差数列的前项和为，，，则数列的通项公式 为 . ‎ ‎7. 在一个袋内装有同样大小、质地的五个球，编号分别为1、2、3、4、5，若从袋中任意 ‎（第9题图）‎ 取两个，则编号的和是奇数的概率为 （结果用最简分数表示）. ‎ ‎8. 在的二项展开式中，常数项等于 .‎ ‎9. 若函数（,）的部分图像如右 图，则 . ‎ ‎10. 在中，若,，则 . ‎ ‎11. 若函数满足，且，则 _.‎ ‎12. 若、，是椭圆上的动点，则 ‎（第13题图）‎ 的最小值为 . ‎ ‎13. 三棱锥中，、、、分别为 ‎、、、的中点，则截面 将三棱锥分成两部分的体积之比为 . ‎ ‎14. 已知函数，设，‎ 若，则的取值范围是 .‎ 二．选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案 ‎15. 已知函数()，则“”是“函数在上是增函数”的…………………………………………………………………………………………（ ）‎ ‎（A）充分非必要条件. （B）必要非充分条件.‎ ‎（C）充要条件. （D）非充分非必要条件. ‎ ‎16. 【理科】双曲线（）的焦点坐标为……………………（ ）‎ ‎（A）. （B）.‎ ‎（C）. （D）. ‎ ‎17. 已知,,若，则的值不可能是…………………（ ）‎ ‎（A）. （B）. （C）. （D）. ‎ ‎18. 如图,四边形是正方形，延长至，使得.若动点从点出发，沿正方形的边按逆时针方向运动一周回到点，其中，下列判断 P ‎（第18题图）‎ 正确的是…………………………………………………………………………………（ ）‎ ‎（A）满足的点必为的中点.‎ ‎（B）满足的点有且只有一个.‎ ‎（C）的最大值为3.‎ ‎（D）的最小值不存在. 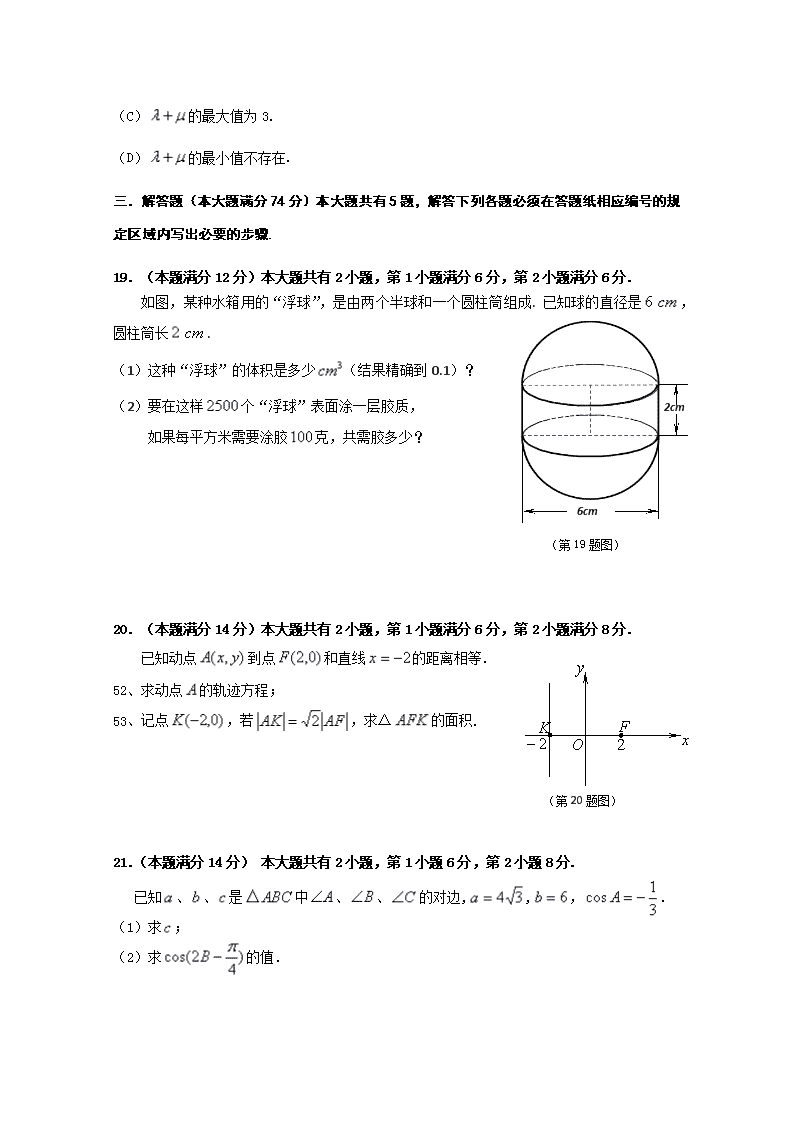‎ 三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.‎ ‎19. （本题满分12分）本大题共有2小题，第1小题满分6分，第2小题满分6分.‎ ‎（第19题图）‎ ‎2cm ‎6cm 如图，某种水箱用的“浮球”，是由两个半球和一个圆柱筒组成. 已知球的直径是，圆柱筒长.‎ ‎（1）这种“浮球”的体积是多少（结果精确到0.1）？‎ ‎（2）要在这样个“浮球”表面涂一层胶质，‎ 如果每平方米需要涂胶克，共需胶多少？‎ ‎20. （本题满分14分）本大题共有2小题，第1小题满分6分，第2小题满分8分.‎ ‎（第20题图）‎ 已知动点到点和直线的距离相等.‎ 52、 求动点的轨迹方程；‎ 53、 记点，若，求△的面积.‎ ‎21.（本题满分14分） 本大题共有2小题，第1小题6分，第2小题8分.‎ 已知、、是中、、的对边,,，．‎ ‎（1）求；‎ ‎（2）求的值．‎ ‎22. （本题满分16分） 本大题共有3小题，第1小题满分5分，第2小题满分5分 ，第3小题满分6分.‎ 在平面直角坐标系中，点满足，且；点满足，且，其中．‎ ‎（1）求的坐标，并证明点在直线上；‎ ‎（2）记四边形的面积为，求的表达式；‎ ‎（3）对于（2）中的，是否存在最小的正整数，使得对任意都有成立？若存在，求的值；若不存在，请说明理由．‎ ‎23.（本题满分18分） 本大题共有3小题，第1小题满分4分，第2小题满分6分 ，第3小题满分8分.‎ 设函数和都是定义在集合上的函数,对于任意的，都有 成立，称函数与在上互为“函数”.‎ ‎（1）函数与在上互为“函数”，求集合；‎ ‎（2）若函数(与在集合上互为 “函数”,‎ 求证：；‎ ‎（3）函数与在集合且，上互为“‎ 函数”，当时,，且在上是偶函数,求函数 在集合上的解析式.‎ 参考答案 一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.‎ ‎1. 2. 3. 4. 5. 6.（） 7. 8.180 9. 10.3 11. 12.1 13. 14.‎ 二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.‎ ‎15.‎ ‎16.‎ ‎17.‎ ‎18.‎ B B D C 三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.‎ ‎19.【解】（1），，…………2分 ‎ ，…………2分 ‎ …………2分 ‎（2）…………2分 ‎ …………2分 ‎ 1个“浮球”的表面积 ‎ 2500个“浮球”的表面积的和 ‎ ‎ 所用胶的质量为（克）…………2分 ‎ 答：这种浮球的体积约为；供需胶克. ‎ ‎20.【解】‎ ‎（1）由题意可知，动点的轨迹为抛物线，其焦点为，准线为 设方程为，其中，即……2分 所以动点的轨迹方程为……2分 ‎（2）过作，垂足为,根据抛物线定义，可得……2分 ‎ 由于，所以是等腰直角三角形 ‎………2分 ‎ 其中…………2分 所以…………2分 ‎21.【解】（1）在中，由余弦定理得，…………2分 ‎ …………2分 即，，解得…………2分 ‎ （2）由得为钝角，所以…………2分 在中， 由正弦定理，得 则…………2分 由于为锐角，则……2分 所以……2分 ‎22【解】（1）由已知条件得，,,所以…2分 ‎，则 设，则，‎ 所以；………2分 即满足方程，所以点在直线上. ……1分 ‎（证明在直线上也可以用数学归纳法证明.）‎ ‎（2）由（1）得 ‎ ………1分 ‎ 设，则，‎ ‎，所以 ‎， 逐差累和得，，‎ 所以………2分 设直线与轴的交点，则 ‎，……2分 ‎（3）由（2），‎ ‎ …2分 于是，， ………2分 数列中项的最大值为，则,即最小的正整数的值为，所以，存在最小的自然数，对一切都有成立.……2分 ‎23.【解】（1）由得 ‎ ‎ 化简得，，或………2分 解得或，，即集合……2分 ‎(若学生写出的答案是集合的非空子集，扣1分，以示区别。)‎ ‎（2）证明：由题意得，（且）………2分 ‎ 变形得，，由于且 ‎ ………2分 因为，所以，即………2分 ‎（3）当，则，由于函数在上是偶函数 则 所以当时， ……………2分 由于与函数在集合上“ 互为函数”‎ 所以当，恒成立,‎ 对于任意的()恒成立,‎ 即……………2分 所以,‎ 即 所以,‎ 当（）时,‎ ‎……………2分 所以当时，‎ ‎………2分