人教版高中数学选修1-1课件：10_《充要条件》(1) 15页

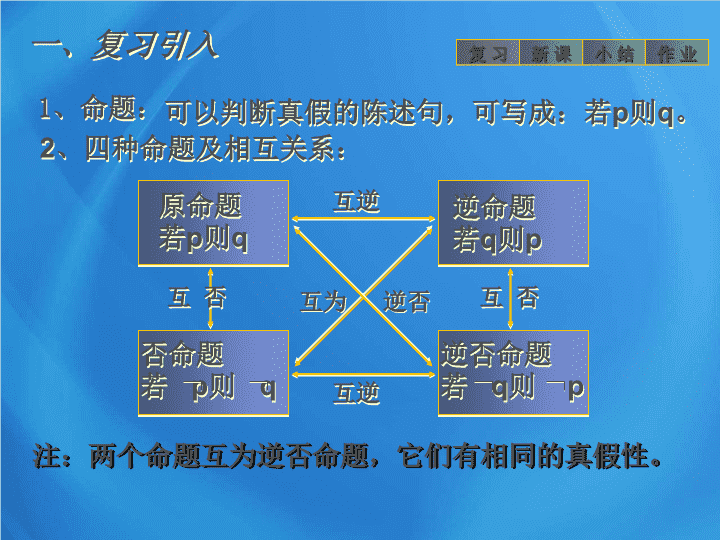
充分条件与 必要条件 高中选修 《 数学 1-1》 （新教材） 复 习 小 结 作 业 新 课 1 、命题： 可以判断真假的陈述句，可写成：若 p 则 q 。 2 、四种命题及相互关系： 一、复习引入 逆命题若 q 则 p 原命题若 p 则 q 否命题若 p 则 q 逆否命题若 q 则 p 互逆 互逆 互 否 互 否 互为 逆否 小 结 作 业 复 习 新 课 注 ： 两个命题互为逆否命题，它们有相同的真假性。 一、复习引入 小 结 作 业 复 习 新 课 3 、例 : 判断下列命题的真假。  （ 1 ）若 x>a 2 +b 2 ，则 x>2ab 。 （ 2 ）若 ab=0, 则 a=0 。 （ 2 ）因为若 ab=0 则应该有 a=0 或 b=0 。 所以并不能得到 a 一定为 0 。 真命题 假命题 解 （ 1 ）因为若 x>a 2 +b 2 ，而 a 2 +b 2 2ab ，所以可以 得到 x>2ab 。 一、复习引入 小 结 作 业 复 习 新 课 4 、例， 将（ 1 ）改写成“若 p ，则 q” 的形式  并判断下列命题的真假及其逆命题的真假。  （ 1 ）有两角相等的三角形是等腰三角形。 （ 2 ）若 a 2 >b 2 ，则 a>b 。 解 （ 1 ）原命题：若一个三角形有两个角相等，则这个 三角形是等腰三角形。 （ 2 ）原命题：若 a 2 >b 2 ，则 a>b 。 逆命题：若一个三角形是等腰三角形，则这个 三 角形有两个角相等。 逆命题：若 a>b ，则 a 2 >b 2 。 真命题 真命题 假命题 假命题 一、复习引入 在真命题（ 1 ）中， p 是 q 成立所 必须具备 的前提。 在假命题（ 2 ）中， p 不是 q 成立所 必须具备 的前提。 在真命题（ 1 ）中， p 足以导致 q ，也就是说条件 p 充分 了。在假命题（ 2 ）中条件 p 不 充分 。 （ 1 ）有两角相等的三角形是等腰三角形。（ 2 ）若 a 2 >b 2 ，则 a>b 。 5 、在原命题中研究条件对结论的制约程度 6 、在逆命题中研究结论对条件的依赖程度 小 结 作 业 复 习 新 课 1 、如果命题“若 p 则 q” 为真，则记作 p q （或 q p ）。 二、新课 小 结 作 业 新 课 复 习 练习 1 用符号 与 填空。 （ 1 ） x 2 =y 2 x=y ；（ 2 ）内错角相等 两直线平行；（ 3 ）整数 a 能被 6 整除 a 的个位数字为偶数；（ 4 ） ac=bc a=b 2 、如果命题“若 p 则 q” 为假，则记作 p q 。 二、新课 定义 2 ：如果已知 q p ，则说 p 是 q 的必要条件。 1 、定义 1 ：如果已知 p q ，则说 p 是 q 的充分条件。 ① p q ，相当于 P Q ，即 P Q 或 P 、 Q ② q p ，相当于 Q P ，即 Q P 或 P 、 Q ③ p q ，相当于 P=Q ，即 P 、 Q 有它就行 缺它不行 同一事物 2 、从集合角度理解： 定义 3 ：如果既有 p q ，又有 q p ，就记作 则说 p 是 q 的充要条件。 p q ， 复 习 小 结 作 业 新 课 二、新课 例 1 ，下列“若 p ，则 q” 形式的命题中，哪些命题  中的 p 是 q 的充分条件？  （ 1 ）若 x=1 ，则 x 2 –4x+3=0 ； （ 2 ）若 f （ x ） =x ，则 f （ x ）为增函数； （ 3 ）若 x 为无理数，则 x 2 为无理数 解 ：命题（ 1 ）（ 2 ）是真命题，命题（ 3 ）是假命题，所以命题（ 1 ）（ 2 ）中的 p 是 q 的充分条件 复 习 小 结 作 业 新 课 如果已知 p q ，则说 p 是 q 的充分  条件， q 是 p 的必要条件。 3 、简化定义： 二、新课 练习 2 下列“若 p ，则 q” 形式的命题中，哪些命题中的 p 是 q 的充分条件？ 复 习 小 结 作 业 新 课 (1) 若两个三角形全等，则这两个三角形相似； (2) 若 x > 5 ，则 x > 10 。 解 ：命题 （ 1 ）是真命题，命题（ 2 ）是假命题 所以命题（ 1 ）中的 p 是 q 的充分条件。 二、新课 复 习 小 结 作 业 新 课 ① 认清条件和结论。 ② 考察 p q 和 q p 的真假。 ① 可先简化命题。 ③ 将命题转化为等价的逆否命题后再判断。 ② 否定一个命题只要举出一个反例即可。 4 、判别步骤： 5 、判别技巧： 判别充分条件与必要条件 二、新课 例 2 下列“若 p ，则 q” 形式的命题中，哪些命题中的 q 是 p 的必要条件？ 复 习 小 结 作 业 新 课 (1) 若 x=y ，则 x 2 =y 2 。 (2) 若两个三角形全等，则这两个三角形的面积相等。 (3) 若 a>b ，则 ac>bc 。 解 ：命题 （ 1 ）（ 2 ）是真命题，命题（ 3 ）是假命题， 所以命题（ 1 ）（ 2 ）中的 q 是 p 的必要条件。 二、新课 练习 3 下列“若 p ，则 q” 形式的命题中，哪些命题中的 p 是 q 的必要条件？ 复 习 小 结 作 业 新 课 (1) 若 a+5 是无理数，则 a 是无理数。 (2) 若（ x-a ）（ x-b ） =0 ，则 x=a 。 解 ：命题 （ 1 ）（ 2 ）的逆命题都是真命题， 所以命题（ 1 ）（ 2 ）中的 p 是 q 的必要条件。 分析 ：注意这里考虑的是命题 中的 p 是 q 的必要条件。 所以应该分析下列命题的逆命题的真假性。 二、新课 复 习 小 结 作 业 新 课 答： 命题 （ 1 ）为真命题： 练习 4 ，判断下列命题的真假： （ 1 ） x=2 是 x 2 –4x+4=0 的必要条件； （ 2 ）圆心到直线的距离等于半径是这条  直线为圆的切线的必要条件； （ 3 ） sin =sin 是 = 的充分条件； （ 4 ） ab 0 是 a 0 的充分条件。 = = 命题（ 2 ）为真命题； 命题（ 3 ）为假命题； 命题（ 4 ）为真命题。 三、小结 如果已知 p q ，则说 p 是 q 的充分  条件， q 是 p 的必要条件。 ① 认清条件和结论。 ② 考察 p q 和 q p 的真假。 ① 可先简化命题。 ③ 将命题转化为等价的逆否命题后再判断。 ② 否定一个命题只要举出一个反例即可。 1 、定义： 2 、判别步骤： 3 、判别技巧： 新 课 复 习 作 业 小 结 四、作业 1 、课本 P15 ， 3 （ 1 ）、（ 3 ）、（ 5 ）。 新 课 复 习 小 结 作 业