2019届二轮复习第6讲　三角函数图象与性质学案（全国通用） 17页

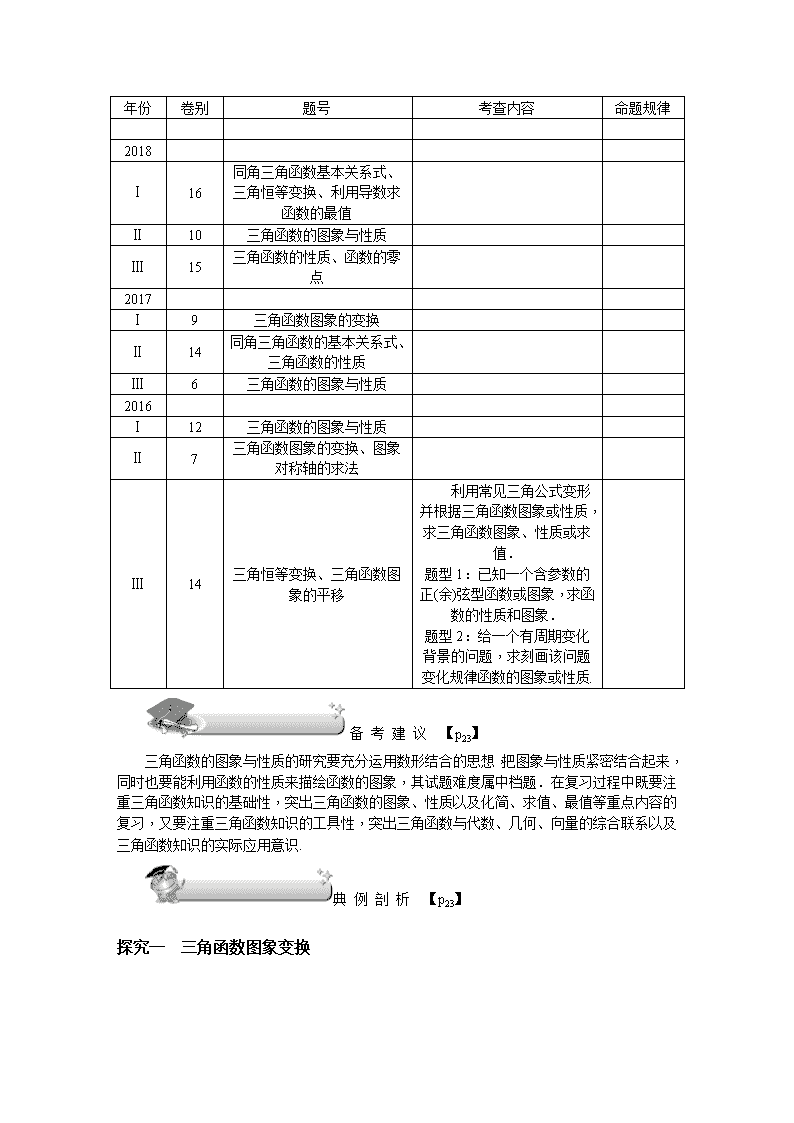
‎(这是边文，请据需要手工删加)‎ 名师导学·高考二轮总复习·理科数学 ‎(这是边文，请据需要手工删加)‎ ‎　专题三　三角函数图象与性质 ‎(这是边文，请据需要手工删加)‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　专　　题　　　三 三角函数图象与性质 第6讲　三角函数图象与性质 　【p23】‎ 　【p23】‎ 年份 卷别 题号 考查内容 命题规律 ‎2018‎ Ⅰ ‎16‎ 同角三角函数基本关系式、三角恒等变换、利用导数求函数的最值 Ⅱ ‎10‎ 三角函数的图象与性质 Ⅲ ‎15‎ 三角函数的性质、函数的零点 ‎2017‎ Ⅰ ‎9‎ 三角函数图象的变换 Ⅱ ‎14‎ 同角三角函数的基本关系式、三角函数的性质 Ⅲ ‎6‎ 三角函数的图象与性质 ‎2016‎ Ⅰ ‎12‎ 三角函数的图象与性质 Ⅱ ‎7‎ 三角函数图象的变换、图象对称轴的求法 Ⅲ ‎14‎ 三角恒等变换、三角函数图象的平移 ‎　　利用常见三角公式变形并根据三角函数图象或性质，求三角函数图象、性质或求值．‎ 题型1：已知一个含参数的正(余)弦型函数或图象，求函数的性质和图象．‎ 题型2：给一个有周期变化背景的问题，求刻画该问题变化规律函数的图象或性质.‎ 备 考 建 议　【p23】‎ 三角函数的图象与性质的研究要充分运用数形结合的思想，把图象与性质紧密结合起来，同时也要能利用函数的性质来描绘函数的图象，其试题难度属中档题．在复习过程中既要注重三角函数知识的基础性，突出三角函数的图象、性质以及化简、求值、最值等重点内容的复习，又要注重三角函数知识的工具性，突出三角函数与代数、几何、向量的综合联系以及三角函数知识的实际应用意识. ‎ 典 例 剖 析　【p23】‎ 探究一　三角函数图象变换 ‎　　　　　　　　　　　　　　　　　　‎ 例1已知曲线C1：y＝cos x，C2：y＝‎ cos，则下面结论正确的是(　　)‎ A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2‎ B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2‎ C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2‎ D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2‎ ‎【解析】选C.‎ 把C1各点的横坐标缩短到原来的倍，纵坐标不变，得到函数y＝cos 2x的图象，再把得到的曲线向右平移个单位长度后，得到y＝cos＝cos的图象，故选C.‎ ‎【点评】对于三角函数图象的平移变换问题，其平移变换规则是“左加、右减”，并且在变换过程中只变换其自变量x，如果x的系数不是1，则需把x的系数提取后再确定平移的单位和方向．另外，当两个函数的名称不同时，首先要将函数名称统一，其次要把ωx＋φ变成ω，最后确定平移的单位并根据的符号确定平移的方向．‎ 探究二　由三角函数图象求解析式 例2 已知奇函数f(x)＝Acos(A>0，ω>0，0<φ<π)的导函数的部分图象如图所示，E是最高点，且△MNE是边长为1的正三角形，那么f＝(　　)‎ A．－ B．－ C. D．－ ‎【解析】选D.‎ 由奇函数f(0)＝0⇒φ＝，△MNE是边长为1的正三角形，可得＝1⇒T＝2⇒ω＝π，E 是最高点且yE＝，f′(x)＝－Aωcos ωx得A＝，所以f(x)＝cos⇒f＝－.‎ ‎【点评】已知函数图象求y＝Asin(ωx＋φ)(A＞0，ω＞0)的解析式时，常用的方法是待定系数法．由图中的最高点、最低点或特殊点求A；由函数的周期确定ω；确定φ常根据“五点法”中的五个点求解，其中一般把第一个零点作为突破口，可以从图象的升降找准第一个零点的位置．‎ 探究三　讨论三角函数的单调性 例3 已知ω＞0，函数f(x)＝sin在区间上单调递减，则ω的取值范围是(　　)‎ A. B. C. D．(0，2]‎ ‎【解析】选A.‎ 解法一：(淘汰法)取ω＝，f(x)＝sin，‎ 其减区间为(k∈Z)．‎ 由⊆(k∈Z)排除B、C，‎ 取ω＝2.同理排除D，故选A.‎ 解法二：由题设x∈时，‎ f′(x)＝ωcos≤0，‎ 即cos≤0恒成立．‎ 又x∈时，‎ ωx＋∈，‎ 则⊆(k∈Z)．‎ 当k＝0时，由 求得≤ω≤，故选A.‎ ‎【点评】分析研究函数的周期性或单调性，应将题设三角函数解析式恒等变形为y＝‎ Asin(ωx＋φ)(ω＞0)型(或y＝Acos(ωx＋φ)，y＝Atan(ωx＋φ)型)，然后再应用相关方法求解．‎ 例4 设函数f(x)＝sin(ωx＋φ)，x∈R，其中ω>0，|φ|<.若f＝1，f＝0，且f(x)的最小正周期大于2π.‎ ‎(1)求函数f(x)的解析表达式；‎ ‎(2)讨论f(x)在区间内的单调性．‎ ‎【解析】(1)由f(x)的最小正周期大于2π，得>，‎ 又f＝1，f＝0得＝＋＝，‎ ‎∴T＝3π，则＝3π，ω＝.‎ ‎∴f(x)＝sin(ωx＋φ)＝sin，‎ 由f＝1，即sin＝1，‎ 得sin＝1.‎ ‎∴＋φ＝＋2kπ，k∈Z.取k＝0，得φ＝<，满足题意．‎ ‎∴ω＝，φ＝.∴函数解析式为f(x)＝sin.‎ ‎(2)当x∈时，x＋∈，‎ ‎∴由－≤x＋≤，得－≤x≤；‎ 由≤x＋≤，得≤x≤，‎ ‎∴ 当x∈时，f(x)的单调递增区间为；单调递减区间为.‎ ‎【点评】研究函数y＝Asin(ωx＋φ)的性质的“两种”意识 ‎(1)转化意识：利用三角恒等变换把待求函数化成y＝Asin(ωx＋φ)＋B的形式．‎ ‎(2)团体意识：类比研究y＝sin x的性质，只需将y＝Asin(ωx＋φ)中的“ωx＋φ”看成y＝sin x中的“x”代入求解便可．‎ 提醒：在求y＝Asin(ωx＋φ)的单调区间时，要特别注意A和ω的符号，必要时通过诱导公式先将ω的符号化为正的．‎ 探究四　求三角函数在闭区间上的最值 ‎(或值域)‎ 例5 已知函数f(x)＝4sin2－2cos 2x－1，且给定条件p：“≤x≤”．‎ ‎(1)求f(x)的最大值及最小值；‎ ‎(2)若又给条件q：“|f(x)－m|＜‎2”‎且p是q的充分条件，求实数m的取值范围．‎ ‎【解析】(1)∵f(x)＝2－2cos 2x－1＝2sin 2x－2cos 2x＋1‎ ‎＝4sin＋1.‎ 又∵≤x≤，∴≤2x－≤，‎ ‎∴3≤4sin＋1≤5.‎ ‎∴f(x)max＝5，f(x)min＝3.‎ ‎(2)∵|f(x)－m|＜2，‎ ‎∴m－2＜f(x)＜m＋2.‎ 又p是q的充分条件，‎ ‎∵ ‎∴3＜m＜5.‎ 例6 已知函数f(x)＝cos＋sin2x－cos2x.设函数g(x)＝[f(x)]2＋f(x)，求g(x)的值域．‎ ‎【解析】f(x)＝cos 2x＋sin 2x－cos 2x＝sin.‎ 故g(x)＝[f(x)]2＋f(x)‎ ‎＝sin2＋sin ‎＝－.‎ 当sin＝－时，‎ g(x)取得最小值－，‎ 当sin＝1时，g(x)取得最大值2，‎ 所以g(x)的值域为.‎ ‎【点评】求三角函数最值的两种思路：(1)将问题化为y＝Asin(ωx＋φ)＋B的形式，结合三角函数的性质或图象求解；(2)将问题化为关于sin x或cos x的二次函数的形式，借助二次函数的性质或图象求解．‎ 规 律 总 结　【p25】‎ ‎1．三角函数的图象与性质的应用问题中用到数形结合思想的常见题型：‎ ‎(1)确定函数的性质；确定某些三角函数的最值(值域)、周期性等性质时，常根据条件作出函数的图象数形结合求解．‎ ‎(2)由图象特点求解析式；求解时根据所给图象由最值点求A，由周期求ω，由特殊点求φ，实现“以形助数”．‎ ‎(3)三角函数零点(或三角方程解)的问题；求解此类问题时，常作出符合要求的图象，‎ 由数形结合法求解．‎ ‎(4)变换法作图；结合函数解析式特征，通过平移变换、伸缩变换、对称变换作出图象，实现“以数辅形”．‎ ‎2．求函数y＝Asin(ωx＋φ)(或y＝Acos(ωx＋φ)或y＝Atan(ωx＋φ))的单调区间的步骤：‎ ‎(1)将ω化为正．‎ ‎(2)将ωx＋φ看成一个整体，由三角函数的单调性求解．‎ ‎3．已知函数y＝Asin(ωx＋φ)＋B(A＞0，ω＞0)的图象求解析式的步骤：‎ ‎(1)A＝，B＝.‎ ‎(2)由函数的周期T求ω.‎ ‎(3)利用与“五点法”中相对应的特殊点求φ.‎ ‎4．三角函数图象与性质解题中失分误区：‎ ‎(1)忽视定义域和名称；求解三角函数的单调区间、最值(值域)以及作图象等问题时，要注意函数的定义域和名称．‎ ‎(2)忽视平移单位；要重视图象变换顺序，在图象变换过程中，注意分清是先相位变换，还是先周期变换．变换只是相对于其中的自变量x而言的，如果x的系数不是1，就要把这个系数提取后再确定变换的单位长度和方向．‎ ‎(3)忽视A，ω的符号，忽视注明k∈Z；在求y＝Asin(ωx＋φ)的单调区间时，要特别注意A和ω的符号，若ω＜0，需先通过诱导公式将x的系数化为正的．‎ 高 考 回 眸　【p25】‎ ‎　　　　　　　　　　　　　　　　　　‎ 考题1[2018·全国卷Ⅰ]已知函数f(x)＝2sin x＋sin 2x，则f(x)的最小值是________．‎ ‎【解析】－ f′(x)＝2cos x＋2cos 2x＝2(2cos x－1)(cos x＋1)，‎ 当cos x<时，f′(x)<0，f(x)单调递减；‎ 当cos x>时，f′(x)>0，f(x)单调递增；‎ 所以当cos x＝时，f(x)有最小值．‎ 又f(x)＝2sin x＋sin 2x＝2sin x(1＋cos x)，‎ 所以当sin x＝－时，f(x)有最小值．‎ 即f(x)min＝2××＝－.‎ ‎【命题立意】本题主要考查了三角函数的最值，导数的应用，考查了考生的转化化归能力、运算求解能力，考查的核心素养是数学运算．‎ 考题2[2018·全国卷Ⅱ]若f(x)＝cos x－sin x在[－a，a]是减函数，则a的最大值是(　　)‎ A. B. C. D．π ‎【解析】选A.‎ f(x)＝cos x－sin x＝－sin，‎ 当x∈，即x－∈时，函数f(x)单调递减，‎ 因为f(x)在[－a，a]是减函数，所以[－a，a]⊆，故a的最大值为，选A.‎ ‎【命题立意】本题考查了三角函数的单调性，三角恒等变换，意在考查考生的逻辑思维能力、等价转换能力、运算求解能力．考查的数学核心素养是逻辑推理、数学运算．‎ 考题3[2018·全国卷Ⅲ]函数f(x)＝‎ cos在[0，π]上的零点的个数为________．‎ ‎【解析】3‎ 由题意可知，当3x＋＝kπ＋(k∈Z)时，‎ f(x)＝cos＝0.‎ 因为x∈[0，π]，‎ 所以3x＋∈，‎ 故当3x＋取值为，，时，‎ f(x)＝cos＝0，‎ 即函数f(x)＝cos在[0，π]上的零点的个数为3.‎ ‎【命题立意】本题考查了三角函数的图象与性质，考查了数形结合思想和考生的运算求解能力．考查的数学核心素养是数学运算．‎ 考点限时训练　【p119】‎ A组　基础演练 ‎1．在区间 范围内，函数y＝tan x与函数y＝sin x的图象交点的个数为(　　)‎ A．1 B．‎2 C．3 D．4‎ ‎【解析】选A.‎ 在同一坐标系中，作出y＝sin x与y＝tan x在内的图象，很难做到精确，容易误认为3个交点．联想到不等式“sin xf(π)，则φ等于(　　)‎ A. B. C. D. ‎【解析】选C.‎ 由f(x)≤可知是函数f(x)的对称轴，所以2×＋φ＝＋kπ，所以φ＝＋kπ，由f>f(π)，得sin(π＋φ)>sin(2π＋φ)，即－sin φ>sin φ，所以sin φ<0，又0<φ<2π，所以π<φ<2π，所以当k＝1时，φ＝.‎ ‎*4.已知ω>0，函数f(x)＝sin在上单调递减，则ω的取值范围是(　　)‎ A. B. C. D. ‎【解析】选B.‎ 由2kπ＋≤ωx＋≤2kπ＋，即2kπ＋≤ωx≤2kπ＋，由0)的图象向右平移个单位长度，所得图象经过点，则ω的最小值是________．‎ ‎【解析】2‎ 函数f(x)的图象向右平移个单位长度得到函数g(x)＝f＝sin＝sin的图象，‎ 因为此时函数图象过点，‎ 所以sin ω＝0，‎ 即ω＝＝kπ(k∈Z)，‎ 所以ω＝2k(k∈Z)，‎ 又ω>0，所以ω的最小值为2.‎ ‎*14.已知函数f(x)＝Acos(ωx＋φ)的部分图象如图所示，与x轴交于A、B两点，与y轴交于P点，其一条对称轴与x轴交于C点，且PA＝PC＝2，PB＝BC，则ω＝________．‎ ‎【解析】 函数周期为，故AB＝T＝，PB＝BC＝＝，AC＝，OA＝OC＝，OB＝OC－BC＝，由于OB＝PB，所以∠OPB＝∠PCB＝∠BPC＝，∠OBP＝，所以＝OC＝PCcos＝3，故ω＝.‎ ‎15．已知函数f(x)＝2sinsin＋sin 2ωx＋a(ω>0)的图象与直线y＝m(m>0)相切，并且切点横坐标依次成公差为π的等差数列，且f(x)的最大值为1.‎ ‎(1)若x∈[0，π]，求函数f(x)的单调递增区间；‎ ‎(2)将f(x)的图象向左平移个单位，得到函数g(x)的图象，若函数y＝g(x)－m在上有零点，求实数m的取值范围．‎ ‎【解析】(1)∵f(x)＝sin＋sin 2ωx＋a ‎＝cos 2ωx＋sin 2ωx＋a＝2sin＋a，‎ 由题意得ω＝1，‎ ‎∴2＋a＝1，所以a＝－1，‎ 所以f(x)＝2sin－1，‎ 由－＋2kπ≤2x＋≤＋2kπ，‎ 解得－＋kπ≤x≤＋kπ，‎ 所以函数f(x)在区间[0，π]上的单调递增区间是和.‎ ‎(2)∵将f(x)的图象向左平移个单位，得到函数g(x)的图象，‎ ‎∴g(x)＝f＝2sin－1‎ ‎＝2sin－1，‎ ‎∵x∈，∴2x＋∈，‎ ‎∴当2x＋＝时，sin＝，g(x)取最大值－1；‎ 当2x＋＝时，sin＝－1，g(x)取最小值－3.‎ 若函数y＝g(x)－m在x∈上有零点，‎ 则－3≤m≤－1.‎ ‎16．某同学用“五点法”画函数f(x)＝Asin(ωx＋φ)＋B在某一个周期内的图象时，列表并填入的部分数据如下表：‎ x x1‎ x2‎ x3‎ ωx＋φ ‎0‎ π ‎2π Asin(ωx＋φ)＋B ‎0‎ ‎0‎ ‎－ ‎0‎ ‎(1)请求出上表中的x1，x2，x3的值，并写出函数f(x)的解析式；‎ ‎(2)将f(x)的图象向右平移个单位得到函数g(x)的图象，若函数g(x)在区间[0，m](30.‎ ‎(1)若y＝f(x)在上单调递增，求ω的取值范围；‎ ‎(2)令ω＝2，将函数y＝f(x)的图象向左平移个单位，再向上平移1个单位，得到函数y＝g(x)的图象，区间[a，b](a，b∈R且a0，根据题意有 ‎ ⇒0<ω≤.‎ ‎(2)f(x)＝2sin 2x，‎ g(x)＝2sin＋1＝2sin＋1.‎ g(x)＝0⇒x＝kπ－或x＝kπ－π，k∈Z，‎ 即g(x)的零点相离间隔依次为和，‎ 故若y＝g(x)在[a，b]上至少含有30个零点，则b－a的最小值为14×＋15×＝.‎ 另一种解法：若b－a最小，则a和b都是零点，此时在区间[a，π＋a]，[a，2π＋a]，…，[a，mπ＋a](m∈N*)上分别恰有3，5，…，‎2m＋1个零点，‎ 所以在区间[a，14π＋a]上恰有29个零点，从而在区间(14π＋a，b]上至少有一个零点，‎ b－a－14π≥，‎ 另一方面，在区间上恰有30个零点，‎ 因此b－a的最小值为14π＋＝.‎