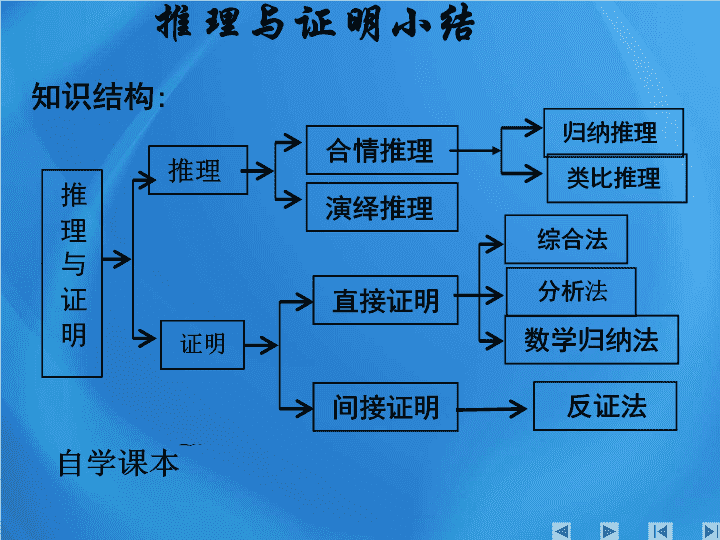
- 601.50 KB
- 2021-06-15 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
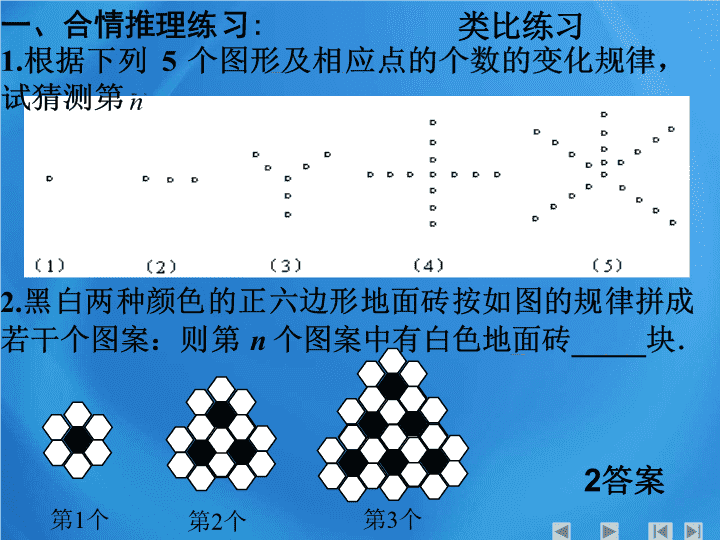
第
1
个
第
2
个
第
3
个
2
答案
类比练习
第
1
个
第
2
个
第
3
个
第
4
个
类比练习
与猜测吻合
!ye!
4.
用数学归纳法证明
:
能被
8
整除
.
综合法
:
巧用
“
1
”
的代换
分析法
:
充分用好条件,不断变形转化!
反证法
4.
用数学归纳法证明
:
能被
8
整除
.
证
:(1)
当
n
=1
时
,5+2+1=8,
命题显然成立
.
(2)
假设当
n
=
k
时
,
A
k
能被
8
整除
,
即
是
8
的倍数
.
那么
:
因为
A
k
是
8
的倍数
,3
k
-
1
+1
是偶数即
4(3
k
-
1
+1)
也是
8
的倍数
,
所以
A
k
+1
也是
8
的倍数
,
即当
n
=
k
+1
时
,
命题成立
.
由
(1)
、
(2)
知对一切正整数
n
,
A
n
能被
8
整除
.