【推荐】专题06 圆锥曲线与方程（导学案）-2017-2018学年上学期期末复习备考高二数学（文）黄金讲练x 12页

一、学习目标：‎ ‎ 1.了解圆锥曲线的实际背景，了解圆锥曲线在刻画现实世界和解决实际问题中的作用.‎ ‎ 2.掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质.‎ ‎ 3.了解双曲线的定义、几何图形和标准方程，知道它的简单几何性质.‎ ‎ 4.了解圆锥曲线的简单应用.‎ ‎ 5.理解数形结合的思想.‎ 二、知识梳理 ‎1、平面内与两个定点，的距离之和等于常数（大于）的点的轨迹称为椭圆．‎ 即：。‎ 这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距．‎ ‎2、椭圆的几何性质：‎ 焦点的位置 焦点在轴上 焦点在轴上 图形 标准方程 范围 且 且 顶点 ‎、‎ ‎、‎ ‎、‎ ‎、‎ 轴长 短轴的长 长轴的长 焦点 ‎、‎ ‎、‎ 焦距 对称性 关于轴、轴、原点对称 离心率 ‎3、平面内与两个定点，的距离之差的绝对值等于常数（小于）的点的轨迹称为双曲线．即：。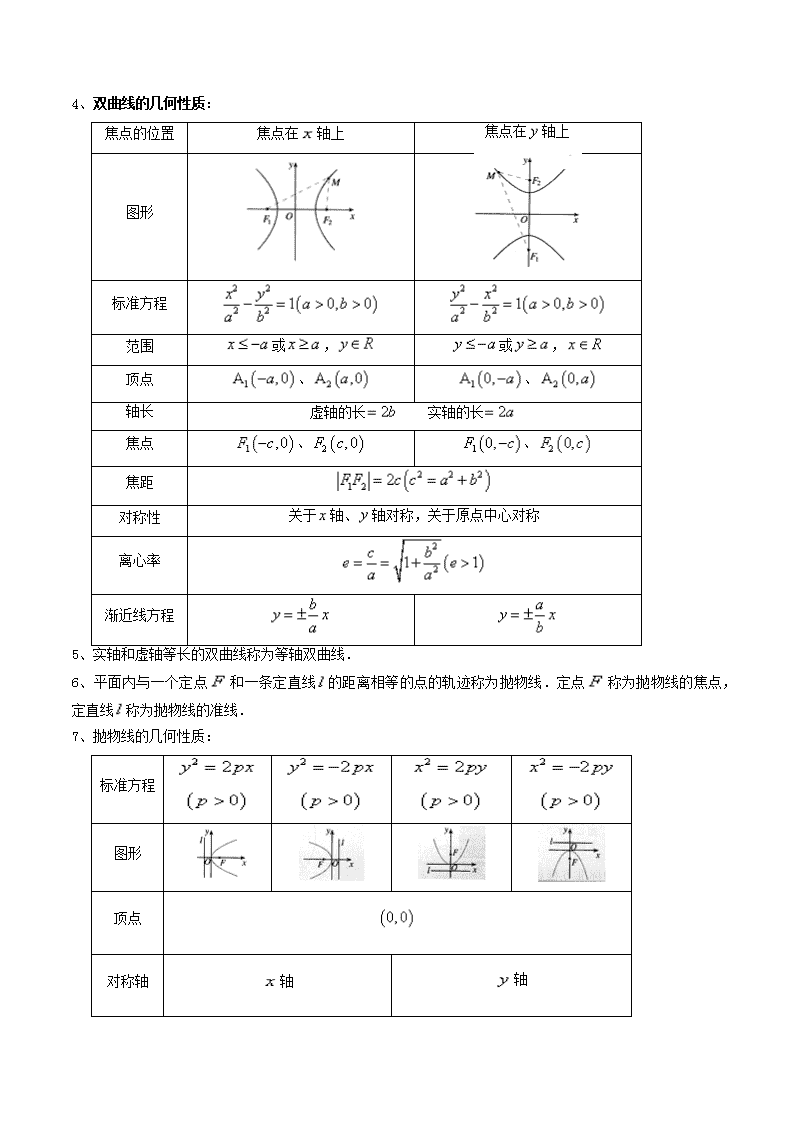‎ 这两个定点称为双曲线的焦点，两焦点的距离称为双曲线的焦距．‎ ‎4、双曲线的几何性质：‎ 焦点的位置 焦点在轴上 焦点在轴上 图形 标准方程 范围 或，‎ 或，‎ 顶点 ‎、‎ ‎、‎ 轴长 虚轴的长 实轴的长 焦点 ‎、‎ ‎、‎ 焦距 对称性 关于轴、轴对称，关于原点中心对称 离心率 渐近线方程 ‎5、实轴和虚轴等长的双曲线称为等轴双曲线．‎ ‎6、平面内与一个定点和一条定直线的距离相等的点的轨迹称为抛物线．定点称为抛物线的焦点，定直线称为抛物线的准线．‎ ‎7、抛物线的几何性质：‎ 标准方程 图形 顶点 对称轴 轴 轴 焦点 准线方程 离心率 范围 ‎8、过抛物线的焦点作垂直于对称轴且交抛物线于、两点的线段，称为抛物线的“通径”，即．‎ 三、典型例题 例1.已知动点M的坐标满足方程5＝|3x＋4y－12|，则动点M的轨迹是(　　)‎ A．椭圆　　　　 B．双曲线 C．抛物线 D．以上都不对 ‎【方法规律】求点的轨迹方程，应结合圆锥曲线的定义。‎ 变式练习1巳知椭圆的中心在坐标原点，长轴在轴上，离心率为，且上一点到的两个焦点的距离之和为12，则椭圆的方程为 ．‎ ‎【答案】 ‎ ‎【解析】，，，，则所求椭圆方程为.‎ 例2.F1，F2是椭圆C1：＋y2＝1与双曲线C2的公共焦点，A，B分别是C1，C2在第二、四象限的公共点．若四边形AF1BF2为矩形，则C2的离心率是(　　)‎ A.　　　　　　B. C. D. ‎【方法规律】求圆锥曲线的离心率，就是从条件中寻找a,b,c之间的关系，再结合，求e＝。‎ 变式练习2.平面直角坐标系中，为椭圆 的四个顶点，为其右焦点，直线与直线相交于点T，线段与椭圆的交点恰为线段的中点，则该椭圆的离心率为 .【答案】‎ ‎【解析】 考查椭圆的基本性质，如顶点、焦点坐标，离心率的计算等。以及直线的方程 直线的方程为：； ‎ 直线的方程为：。二者联立解得：，w.w.w..c.o.m ‎ 则在椭圆上，‎ ‎，w.w.w..c.o.m ‎ 解得：‎ 例3.已知椭圆＋＝1(a>b>0)经过点(0，)，离心率为，左、右焦点分别为F1(－c，0)，F2(c，0)．‎ ‎(1)求椭圆的方程；‎ ‎(2)若直线l：y＝－x＋m与椭圆交于A，B两点，与以F1F2为直径的圆交于C，D两点，且满足＝，求直线l的方程.‎ ‎【分析】(1)利用定义解题．(2)利用勾股定理和弦长公式来解．‎ 由＝，得＝1，解得m＝±，满足(*)．‎ ‎∴直线l的方程为y＝－x＋或y＝－x－.‎ 变式练习3:已知椭圆E：＋＝1(a＞b＞0)，其焦点为F1，F2，离心率为，直线l：x＋2y－2＝0与x轴，y轴分别交于点A，B. ‎ ‎(1)若点A是椭圆E的一个顶点，求椭圆的方程；‎ ‎(2)若线段AB上存在点P满足|PF1|＋|PF2|＝2a，求a的取值范围．‎ ‎【方法规律】直线与圆锥曲线的位置关系主要有：‎ ‎(1)有关直线与圆锥曲线公共点的个数问题，应注意数形结合；‎ ‎(2)有关弦长问题，应注意运用弦长公式及根与系数的关系；‎ ‎(3)有关垂直问题，应注意运用斜率关系及根与系数的关系，尽量设而不求，简化运算．‎ 例4.已知椭圆C经过点A，两个焦点为(－1，0)，(1，0)．‎ ‎(1)求椭圆C的方程；‎ ‎(2)E，F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值．‎ ‎【解析】(1)由题意，c＝1，设椭圆的方程为＋＝1.‎ ‎【方法规律】求曲线方程的常用方法有：‎ ‎(1)直接法：建立适当的坐标系，设动点为(x，y)，根据几何条件直接寻求x，y之间的关系式．‎ ‎(2)代入法：利用所求曲线上的动点与某一已知曲线上的动点的关系，把所求动点转换为已知动点．具体地说，就是用所求动点的坐标x，y来表示已知动点的坐标并代入已知动点满足的曲线的方程，由此即可求得所求动点坐标x，y之间的关系式．‎ ‎(3)定义法：如果所给几何条件正好符合圆、椭圆、双曲线、抛物线等曲线的定义，则可直接利用这些已知曲线的方程写出动点的轨迹方程．‎ 变式练习4.以知椭圆的两个焦点分别为，过点的直线与椭圆相交与两点，且 ‎（1）求椭圆的离心率；‎ ‎（2）求直线AB的斜率；‎ ‎ （3）设点C与点A关于坐标原点对称，直线上有一点在的外接圆上，‎ 求的值 ‎（1）解：由//且，得，从而 ‎.‎ 直线的方程为，于是点H（m，n）的坐标满足方程组 ‎ ， 由解得故 当时，同理可得. ‎ 三、 课堂练习 ‎1.设P是椭圆＋＝1上的点．若F1，F2是椭圆的两个焦点，则|PF1|＋|PF2|等于(　　)‎ A．4 B．5 C．8 D．10‎ ‎【答案】　D ‎【解析】由题可知a＝5，P为椭圆上一点，∴|PF1|＋|PF2|＝2a＝10.故选D。‎ ‎2.在抛物线上,横坐标为4的点到焦点的距离为5,则的值为( )‎ A. B.1 C. D.4‎ ‎【答案】　A ‎ ‎【解析】 抛物线的标准方程为,由抛物线的定义知,解得。故选A.‎ ‎3.若直线经过抛物线的焦点,则实数=__________．‎ ‎【答案】　-1‎ ‎【解析】直线经过抛物线的焦点,则 ‎4.过抛物线的焦点引一直线,已知直线被抛物线截得的弦被焦点分成2:1,求这条直线的方程.．‎ ‎【答案】见解析 四、课后练习 ‎1.双曲线3mx2－my2＝3的一个焦点是(0,2)，则m的值是(　　)‎ A ．－1 B．1 C．－ D. ‎【答案】　A ‎【解析】把方程化为标准形式－＋＝1，‎ ‎∴a2＝－，b2＝－.∴c2＝－－＝4，解得m＝－1.故选A。‎ ‎2.已知双曲线－＝1(a>0，b>0)的一条渐近线方程是y＝x，它的一个焦点在抛物线y2＝24x的准线上，则双曲线的方程为(　　)‎ A.－＝1 B.－＝1 C.－＝1 D.－＝1‎ ‎【答案】　B ‎【解析】本题主要考查双曲线与抛物线的几何性质与标准方程，属于容易题．‎ 依题意知⇒a2＝9，b2＝27，‎ 所以双曲线的方程为－＝1.故选B。‎ ‎3.过抛物线的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则等于(　 )‎ A.2　　　　　B.4　　　　　 C.6　　　　　　D.8‎ ‎【答案】　D ‎【解析】易知线段AB的中点到准线的距离为4,设A,B两点到准线的距离分别为由抛物线的定义知。故选D。‎ ‎4.一个动圆的圆心在抛物线上,且动圆恒与直线相切,则动圆必过定点(　 )‎ A. B. C. D.‎ ‎【答案】C ‎5.若双曲线－＝1(b>0)的渐近线方程为y＝±x，则b等于________．‎ ‎【答案】　1‎ ‎【解析】由题意知＝，解得b＝1.‎ ‎6.设F1和F2是双曲线－y2＝1的两个焦点，点P在双曲线上，且满足∠F1PF2＝90°，则△F1PF2的面积为________．‎ ‎【答案】　1‎ ‎【解析】由题设知 ‎②－①2得|PF1|·|PF2|＝2.∴△F1PF2的面积S＝|PF1|·|PF2|＝1.‎ ‎7.求与椭圆4x2＋9y2＝36有相同的焦距，且离心率为的椭圆的标准方程．‎ ‎【答案】＋＝1，或＋＝1.‎ ‎8.如图,直线与抛物线交于两点,与轴相交于点,且.‎ ‎(1)求证:点的坐标为;‎ ‎(2)求证:;‎ ‎(3)求的面积的最小值.‎ ‎【答案】(3) 1‎ ‎【解析】解:(1) 设点的坐标为, 直线方程为, 代入得 ‎ ① 是此方程的两根,‎ ‎∴,即点的坐标为(1, 0). ‎