- 403.00 KB
- 2021-06-15 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2.3.2
离散型随机变量的方差(二)
高二数学 选修
2-3
知识回顾
★
求离散型随机变量的期望、方差通常有哪些步骤?
★
在解决上述问题中经常要用到哪些性质、公式?
求分布列→求期望→求方差
★
分布列性质
1
、设随机变量
X
的分布列为
P(x=k)=1/4,k=1,2,3,4,
则
EX=
。
2
、若
X
是离散型随机变量,则
E(X-EX)
的值是
。
A.EX B.2EX C.0 D.(EX)
3
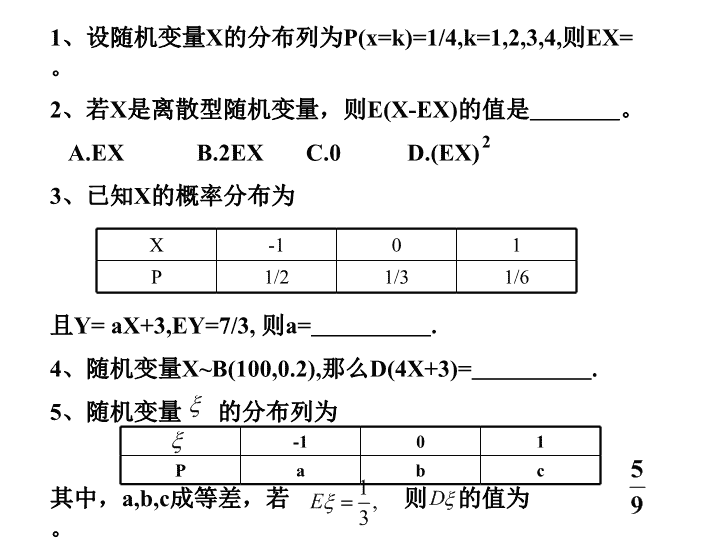
、已知
X
的概率分布为
且
Y= aX+3,EY=7/3,
则
a=
.
4
、随机变量
X~B(100,0.2),
那么
D(4X+3)=
.
5
、随机变量 的分布列为
其中,
a,b,c
成等差,若 则 的值为
。
2
X
-1
0
1
P
1/2
1/3
1/6
-1
0
1
P
a
b
c
6.
根据统计,一年中一个家庭万元以上的财产被盗的概率为
0.01
,保险公司开办一年期万元以上家庭财产保险,参加者需交保险费
100
元,若在一年以内,万元以上财产被盗,保险公司赔偿
a
元(
a>100
),问
a
如何确定,可使保险公司期望获利?
7
、每人交保险费
1000
元,出险概率为
3%
,若保险公司的赔偿金为
a
(
a
>
1000
)元,为使保险公司收益的期望值不低于
a
的百分之七,则保险公司应将最大赔偿金定为多少元?
8
、设
X
是一个离散型随机变量 ,其概率分布为
求
: (
1
)
q
的值;(
2
)
EX
,
DX
。
X
-1
0
1
P
1/2
1-2q
9.
(
07
全国)某商场经销某商品,根据以往资料统计,顾客采用的分起付款期数 的分布列为:
1
2
3
4
5
P
0.4
0.2
0.2
0.1
0.1
商场经销一件该商品,采用
1
期付款,其利润为
200
元,分
2
期或
3
期付款,其利润为
250
元,分
4
期或
5
期付款,其利润为
300
元, 表示经销一件该商品的利润。
(
1
)求事件
A
:”购买该商品的
3
位顾客中,至少有一位采用
1
期付款” 的概率
P(A)
;
(
2
)求 的分布列及期望
E
。
析
:
审清题意是解决该题的关键
.
1.
抓住蝇子一个个有顺序地飞出
,
易联想到把
8
只蝇子看作
8
个元素有序排列
.
●●☆●●●☆●
,由于
ξ=0“
表示☆ ●●●●●☆●”,最后一只必为
果蝇,所以有
ξ=1“
表示 ● ☆ ●●●☆●●”
P
(
ξ=0
)
=
,同理有
P
(
ξ=1
)
=
ξ=2“
表示 ● ● ☆ ●●☆●●”有
P
(
ξ=2
)
=
ξ=3“
表示 ● ● ● ☆ ●☆●●”有
P
(
ξ=3
)
=
ξ=4“
表示 ● ● ●●☆● ☆ ●”有
P
(
ξ=4
)
=
ξ=5“
表示 ● ● ●●● ☆ ☆ ●”有
P
(
ξ=5
)
=
ξ=6“
表示 ● ● ●●●● ☆ ☆”有
P
(
ξ=6
)
=
0
1
2
3
4
5
6
11
、(
07
,重庆)某单位有三辆汽车参加某种事故保险,单位年初向保险公司交纳
900
元的保险金,对在一年内发生此种事故的每辆汽车,单位可获
9000
元的赔偿(假设每辆车最多只赔偿一次)。设这三辆车在一年内发生此种事故的概率分别为
1/9
、
1/10
、
1/11
,且各车是否发生事故相互独立,求一年内该单位在此保险中:
(
1
)获赔的概率;
(
2
)或赔金额 的分布列与期望。
12
、若随机事件
A
在一次试验中发生的概率为
p(0