广东省梅州市2020届高三上学期第一次质量检测 数学（理） 10页

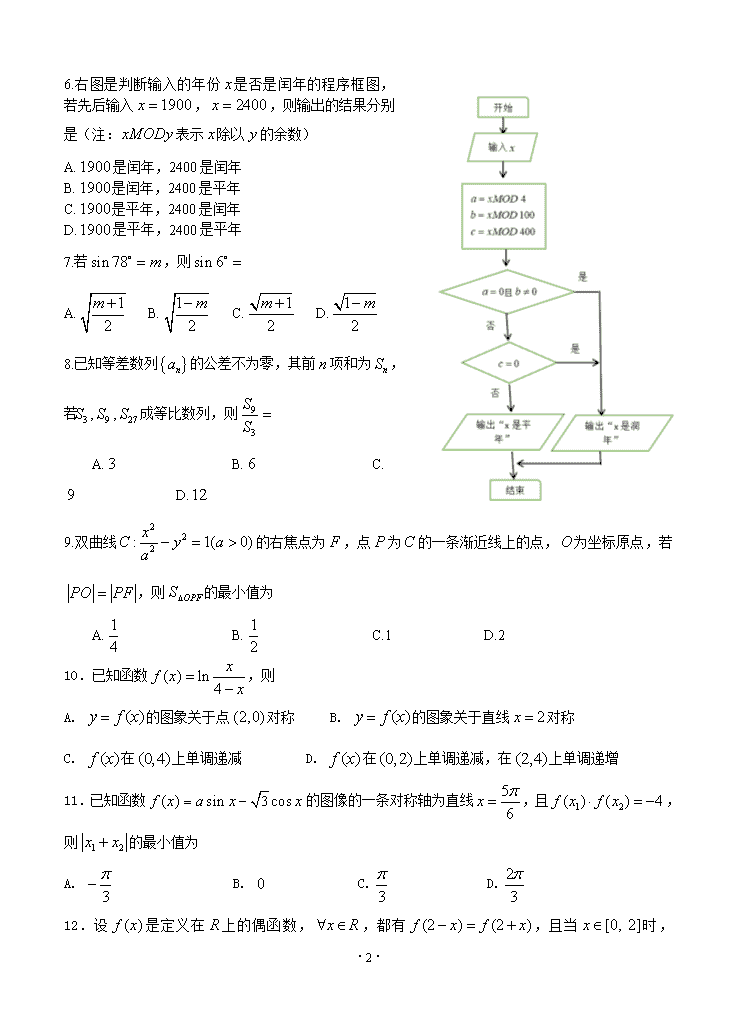
梅州市2020届高三上学期第一次质量检测 理科数学 ‎ 总分：150分 完成时间：120分钟 2019.10‎ 班级 姓名 座号 成绩 ‎ 一．选择题（60分）‎ ‎1.已知集合，，则 ‎ A. B. C. D.‎ ‎2.已知，是关于的方程的一个根，则 A. B. C. D.‎ ‎3.已知，，，则，，的大小关系为 A. B. C. D.‎ ‎4.函数的图象大致为 A. B.‎ C. D.‎ ‎5.右图来自古希腊数学家希波克拉底所研究的几何图形，此图由一个半圆和一个四分之一圆构成，两个阴影部分分别标记为和.在此图内任取一点，此点取自区域的概率记为，取自区域的概率记为，则 A. B. ‎ C. D.与的大小关系与半径长度有关 ‎·10·‎ ‎6.右图是判断输入的年份是否是闰年的程序框图，若先后输入，，则输出的结果分别是（注：表示除以的余数）‎ A.是闰年，2400是闰年 B.是闰年，2400是平年 C.是平年，2400是闰年 ‎ D.是平年，2400是平年 ‎7.若，则 A. B. C. D.‎ ‎8.已知等差数列的公差不为零，其前项和为，若,,成等比数列，则 A. B. C. D.‎ ‎9.双曲线的右焦点为，点为的一条渐近线上的点，为坐标原点，若，则的最小值为 A. B. C.1 D.2‎ ‎10．已知函数，则 A. 的图象关于点对称 B. 的图象关于直线对称 C. 在上单调递减 D. 在上单调递减，在上单调递增 ‎ ‎11．已知函数的图像的一条对称轴为直线，且，则的最小值为 A. B. C. D. ‎ ‎12．设是定义在上的偶函数，，都有，且当时，‎ ‎·10·‎ ‎，函数在区间内恰有三个不同零点，则实数的取值范围是 A． B. ‎ C. D. ‎ 二、填空题（共20分）‎ ‎13.若满足约束条件，则的最大值为______.‎ ‎14.已知是夹角为60°的两个单位向量，，则_____.‎ ‎15.已知函数，若在上恰有3个极值点，则的取值范围是______.‎ ‎16.在三棱锥中，点到底面的距离为，则三棱锥的外接球的表面积为________.‎ 三．（解答题，共70分）‎ ‎17.（12分）的内角所对的边分别为，已知的面积为.‎ ‎（1）证明：‎ ‎（2）若求 ‎18.（12分）某音乐院校举行“校园之星”评选活动，评委由本校全体学生组成，对两位选手，随机调查了20个学生的评分，得到下面的茎叶图：‎ ‎·10·‎ ‎（1）通过茎叶图比较两位选手所得分数的平均值及分散程度（不要求计算出具体值，得出结论即可）；‎ ‎（2）校方将会根据评分记过对参赛选手进行三向分流：‎ 记事件“A获得的分流等级高于B”，根据所给数据，以事件发生的频率作为相应事件发生的概率，求事件C发生的概率.‎ ‎19.（12分）如图，在四棱锥中，底面是矩形，侧棱底面，，点是的中点.‎ （1） 求证：平面；‎ （2） 若直线与平面所成角为，求二面角的大小.‎ ‎20.（12分）已知为抛物线的焦点，直线与相交于两点.‎ ‎（1）若，求的值；‎ ‎（2）点，若，求直线的方程.‎ ‎21.（12分）‎ 已知函数，，为的导数，且.‎ 证明：‎ ‎·10·‎ ‎（1）在内有唯一零点；‎ ‎（2）.‎ ‎（参考数据：，，，，.）‎ ‎（二）选考题：共10分.请考生在第（22），（23）题中任选一题作答，如果多做，则按所做的第一题计分.‎ ‎22.[选修：坐标系与参数方程]（10分）‎ 在极坐标系中，圆.以极点为原点，极轴为轴正半轴建立直角坐标系，直线经过点且倾斜角为.‎ ‎（1）求圆的直角坐标方程和直线的参数方程；‎ ‎（2）已知直线与圆交与，，满足为的中点，求.‎ ‎23.[选修：不等式选讲]（10分）‎ 设函数.‎ ‎（1）画出的图像；‎ ‎（2）若，求的最小值.‎ ‎·10·‎ ‎ ‎ ‎2019-2020学年第一学期高三第一次质检 理科数学参考答案2019.10‎ 一．选择题：CADDC CBCBA DC 二．填空题：‎ ‎（13）0 （14） （15）(，] （16）6p 三．解答题：‎ ‎17．解：（1）由S＝bcsinA＝b2tanA得3csinA＝btanA．‎ ‎ 因为tanA＝，所以3csinA＝，‎ 又因为0＜A＜π，所以 sinA≠0， 因此b＝3ccosA． …4分 ‎（2）因为tanA＝2，所以cosA＝，‎ 由（1）得2bccosA＝，c＝． …8分 由余弦定理得8＝b2＋c2－2bccosA， 所以8＝b2＋－＝，从而b2＝9． 故S＝b2tanA＝3． …12分 ‎ ‎18．解：（1）通过茎叶图可以看出，A选手所得分数的平均值高于B选手所得分数的平均值；A选手所得分数比较集中，B选手所得分数比较分散． …4分 ‎（2）记CA1表示事件：“A选手直接晋级”，CA2表示事件：“A选手复赛待选”；‎ CB1表示事件：“B选手复赛待选”，CB2表示事件：“B选手淘汰出局”．‎ 则CA1与CB1独立，CA2与CB2独立，CA1与CA2互斥，C＝(CA1CB1)∪(CA1CB2)∪(CA2CB2)．‎ P(C)＝P(CA1CB1)＋P (CA1CB2)＋P(CA2CB2) ＝P(CA1)P(CB1)＋P(CA1)P(CB2)＋P(CA2)P(CB2)．‎ 由所给数据得CA1，CA2，CB1，CB2发生的频率分别为，，，，故 A B C E D P O y z x P(CA1)＝，P(CA2)＝，P(CB1)＝，P(CB2)＝，‎ P(C)＝×＋×＋×＝． …12分 ‎19．解：‎ ‎（1）连接AC交BD于O，连接OE．‎ 由题意可知，PE＝EC，AO＝OC，‎ ‎·10·‎ ‎∴PA∥EO，又PAË平面BED，EOÌ平面BED，‎ ‎∴PA∥平面BED． …4分 ‎（2）以D为坐标原点，DA，DC，DP所在直线分别为x轴，y轴，z轴，建立空间直角坐标系D－xyz，设PD＝CD＝1，AD＝a，‎ 则A(a，0，0)，B(a，1，0)，C(0，1，0)，P(0，0，1)，＝(a，1，0)， ＝(a，1，－1)，＝(0，1，－1)‎ 设平面PBC的法向量n＝(x，y，z)，‎ 由得取n＝(0，1，1)． …7分 直线BD与平面PBC所成的角为30°，得 ‎|cosá，nñ|＝＝＝，解得a＝1． …9分 同理可得平面PBD的法向量m＝(－1，1，0)， …10分 cosán，mñ＝＝＝，‎ ‎∵二面角C−PB−D为锐二面角，‎ ‎∴二面角C−PB−D的大小为60°． …12分 ‎20．解：‎ ‎（1）由已知可得F(0，1)，设A(x1，)，B(x2，)，‎ y＝kx＋2与x2＝4y联立得，x2－4kx－8＝0，‎ x1＋x2＝4k， ①‎ x1x2＝－8． ② …2分 ‎|FA|＋|FB|＝＋1＋＋1 ＝＋2． …4分 当k＝1时，由①②得|FA|＋|FB|＝10 …5分 ‎（2）由题意可知，＝(x1，－1)，＝(x2，－1)，＝(－3，－3). ‎ ‎∠CFA＝∠CFB等价cosá，ñ＝cosá，ñ， …8分 又|‎ ‎·10·‎ FA|＝＋1，|FB|＝＋1则 ‎ ＝，整理得4＋2(x1＋x2)－x1x2＝0，‎ 解得k＝－， …11分 所以，直线l的方程为3x＋2y－4＝0． …12分21．解：‎ ‎（1）g(x)＝f¢(x)＝xcosx＋sinx，‎ 所以x∈(0，]时，g(x)＞0，即g(x)在(0，]内没有零点． …2分 x∈(，π)时，g¢(x)＝2cosx－xsinx， 因为cosx＜0，xsinx＞0，从而g¢(x)＜0， 所以g(x)在(，π)上单调递减， 又g(2)＝(2＋tan2)cos2＞0，g()＝－＋＜0， 所以g(x)在(2，)内有唯一零点t． …6分 ‎（2）由（1）得，‎ x∈(0，t)时，g(x)＞0，所以f¢(x)＞0，即f(x)单调递增； x∈(t，π)时，g(x)＜0，所以f¢(x)＜0，即f(x)单调递减，‎ 即f(x)的最大值为f(t)＝tsint． 由f¢(t)＝tcost＋sint＝0得t＝－tant， 所以f(t)＝－tant·sint， 因此f(t)－2＝ ‎＝ ＝． …9分 因为t∈(2，)，所以cost∈(－，cos2)，‎ 从而(cos2－1)2－2＝(－1.4161)2－()2＞0， 即 ‎·10·‎ ＜0， 所以f(t)－2＜0， 故f(x)＜2． …12分 ‎22．解：‎ ‎（1）由圆C：ρ＝4cosθ可得ρ2＝4ρcosθ，‎ 因为ρ2＝x2＋y2，x＝ρcosθ， 所以x2＋y2＝4x，即(x－2)2＋y2＝4．‎ 直线l：（t为参数，0≤α＜π）． …5分 ‎（2）设A，B对应的参数分别为tA，tB，‎ 将直线l的方程代入C并整理，得t2－6t(sinα＋cosα)＋32＝0， 所以tA＋tB＝6(sinα＋cosα)，tA·tB＝32． 又A为MB的中点，所以tB＝2tA， 因此tA＝2(sinα＋cosα)＝4sin(α＋)，tB＝8sin(α＋)， …8分 所以tA·tB＝32sin2(α＋)＝32，即sin2(α＋)＝1． 因为0≤α＜π，所以≤α＋＜， 从而α＋＝，即α＝． …10分 ‎23．解：‎ ‎（1）f(x)＝ …3分 y＝f(x)的图象如图所示： ‎ ‎·10·‎ x y O ‎1‎ ‎1‎ ‎ …5分 ‎（2）一方面，由f(x)≤m|x|＋n得f(0)≤n，解得n≥2．‎ 因为f(x)≥|(2x－1)＋(x＋1)|＝3|x|，所以m|x|＋n≥3|x|．（※）‎ 若m≥3，（※）式明显成立；若m＜3，则当|x|＞时，（※）式不成立． …8分 另一方面，由图可知，当m≥3，且n≥2时，f(x)≤m|x|＋n．‎ 故当且仅当m≥3，且n≥2时，f(x)≤m|x|＋n．‎ 因此m＋n的最小值为5． …10分 ‎·10·‎