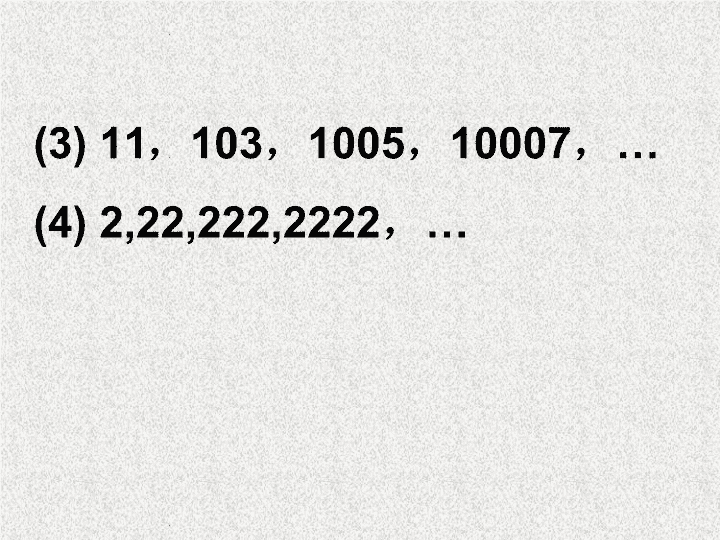2020届二轮复习数列基础概念课件（全国通用） 15页

数列（ 1 ） 1 、写出数列的一个通项公式，使它的前 4 项满足下列各数 ⑴1,3 ， 7,15… 通项： 项与序号的关系一看（符号、式）二验 一、由数列求通项 (3) 11 ， 103 ， 1005 ， 10007 ， … (4) 2,22,222,2222 ， … 1 ：数列｛ a n ｝中 a 1 =2 ，则 a 4 = 　 基础的“代”，综合的“化” 二、由数列递推公式求通项 2 ：在数列 {an} 中， a 1 =3,a n+1 =a n 2 , 则 a n 等于 ____ 3 ：已知 a 1 =1, a n ＝ 1 ＋ 4 ：数列 {a n } 中，已知 a 1 =1, a n >0 (n+1)a n+1 2 -a n 2 +na n+1 .a n =0, 则 a n 等于（ ） 则 a 5 =________________ 6 、数列 {a n } 中， a 1 =1, 对于所有的 n≥2, 都有 a 1 a 2 a 3 …a n =n 2 , 则 a 3 +a 5 = A 61/16 B 25/9 C25/16 D31/15 5 ：在数列 {a n } 中，已知 a 1 =1,a 2 =5, a n+2 =a n+1 -a n , 则 a 1994 等于（ ） A - 4 B - 5 C 4 D 5 三、由数列的和求通项公式 1: 若数列｛ a n ｝的前 n 项的公式为 S n ＝ log 3 （ n ＋ 1 ），则 a 5 等于 A.log 5 6 B.log 3 6/5 C.log 3 6 .log 3 5 2: 数列｛ a n ｝的前 n 项和 S n ＝ n 2 － 7n － 8 （ 1 ）求｛ a n ｝的通项公式 ⑵求｛｜ a n | ｝的前 n 项和 T n 3: 设正数数列｛ a n ｝前 n 项和为 S n ，且存在正数 t ，使得对所有自然数 n ，有 则通过归纳猜想可得到 S n =____ 四、项的性质 函数观（定义域） 1. 数列 {-2n 2 +29n+3} 中的最大项 A 107 B 108 C 108+1/8 D 109 2 、已知｛ a n ｝是递增数列，且对任意 n∈N* 都有 a n =n 2 ＋ λn 恒正，则实数 λ 的取值范围是 A.(-7/2 ， ＋∞） B. （ 0 ，＋∞） C. （－ 2 ，＋∞） D. （－ 3 ，＋∞） A.10 B.11 C.10 或 11 D.12 五、项的单调性 2 、 f (x) ＝ log 2 x － log x 4 (0 ＜ x ＜ 1) ，又知数列｛ a n ｝的通项 a n 满足 f (2a n ) ＝ 2n （ n∈N* ） 1 ）试求数列｛ a n ｝的通项表达式 2 ）判断数列｛ a n ｝的增减性 六、综合： 1 、已知数列｛ a n ｝的前 n 项和为 S n ，满足条件 lgS n ＋（ n － 1 ） lgb ＝ lg （ b n+1 ＋ n － 2 ） , 其中 b ＞ 0 ，且 b≠1 （ 1 ）求数列｛ a n ｝的通项公式 （ 2 ）若对 n∈N*, n≥4 时， 恒有 a n ＋ 1 ＞ a n ，试求 b 的取值范围