2019-2020学年江西省宜春市高一上学期期末考试数学试卷 10页

江西省宜春市2019-2020学年高一上学期期末考试数学试卷 一、选择题：本题共 12 小题，每题 5 分，共 60 分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．已知集合 A = {x y = log (x + 1)}， B = ìx Î N 2 + x £ 0ü ，则 A Ç B = （ ）‎ ‎ ‎ î þ ‎2 í x - 3 ý A． {0,1, 2} B． (-1, 3)‎ C．{2, 3} D．{1, 2} 2. 用一个平面去截四棱锥，不可能得到（ ）‎ A．棱锥 B．棱柱 C．棱台 D．四面体 3. 已知圆心(2, -3) ，一条直径的两个端点恰好在两坐标轴上，则这个圆的方程是（ ）‎ A． x2 + y2 - 4x + 6 y + 8 = 0 B． x2 + y2 - 4x + 6 y - 8 = 0‎ C． x2 + y2 - 4x - 6 y = 0 D． x2 + y2 - 4x + 6 y = 0‎ ‎4．若 f (x -1) 的定义域为[1, 2]，则 f (x + 2) 的定义域为（ ） ‎ A． [0,1] ‎‎ B．[-2, -1] C．[2, 3] D．无法确定 ‎ 5. 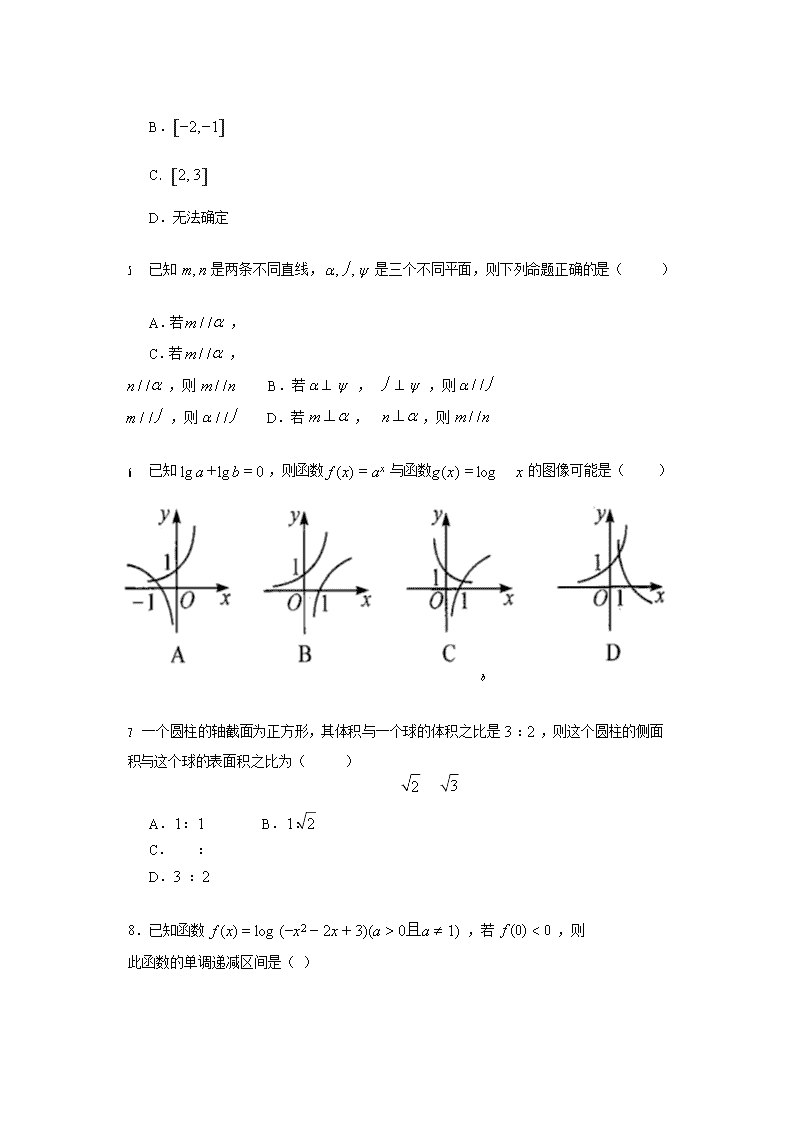已知m, n 是两条不同直线，a , þ , y 是三个不同平面，则下列命题正确的是（ ）‎ A．若 m / /a ，‎ C．若 m / /a ，‎ n / /a ，则m / /n B．若a ^ y ， þ ^ y ，则a / /þ m / /þ ，则a / /þ D．若m ^ a ， n ^ a ，则m / /n 6. 已知lg a + lg b = 0 ，则函数 f (x) = ax 与函数 g(x) = log x 的图像可能是（ ）‎ b ‎2‎ ‎3‎ 7. 一个圆柱的轴截面为正方形，其体积与一个球的体积之比是3 ： 2 ，则这个圆柱的侧面积与这个球的表面积之比为（ ）‎ ‎2‎ A．1：1 B．1：‎ C． ：‎ D． 3 ： 2‎ ‎8．已知函数 f (x) = log (-x2 - 2x + 3)(a > 0且a ¹ 1) ，若 f (0) < 0 ，则 ‎ 此函数的单调递减区间是（ ） ‎ A． (-¥, -1] B．[-1, +¥ ) C． [-1,1) D． (-3, -1] ‎9．若 x, y 满足 x2 + y2 - 2x + 4 y - 20 = 0 ，则 x2 + y2 的最小值是（ ）‎ ‎5‎ A． - 5‎ B． 5 - C． 30 - 10‎ D．无法确定 ‎ ‎5‎ ‎5‎ 10. 下列四个说法中，正确的说法有（ ）个 ‎ ‎①设r > 0 ，则圆(x - 1)2 + (y + 3)2 = r 2 与 x 2 + y 2 = 16 不可能外切； ‎ ‎②集合 A = {x |1 < x < 4}, B={x | x < a} ，若 A † B = B ,则a 的取值范围是[4，+¥) ； ‎ ‎③过点M (-3,5) 且在两坐标轴上的截距互为相反数的直线方程为 x - y +8 = 0 ； ‎ ‎5‎ ‎④直线 x + 2 y + 3 = 0 与直线2x + 4 y +1 = 0 的距离是 . ‎ ‎2‎ A．1 B． 2 C． 3 D． 4 11．如图，网格纸上正方形小格的边长为1，图中粗线画出 的是某几何体的三视图，则该几何体的体积为（ ） ‎ ‎2 4‎ A. B．‎ ‎3 3‎ ‎8‎ C． 3 D． 4‎ 主视图 俯视图 侧视图 ‎12．函数 f (x) 的定义域为 D，若满足：① f (x) 在 D 内是单调函数；②存在[m, n] Í D 使 f (x)‎ ê ú 在[m, n] 上的值域为é m , n ù ，那么就称 y = f (x) 为“成功函数”，若函数 ë 2 2 û f (x) = log (ax + t) ，（ a > 0且a ¹ 1 ）是“成功函数”，则t 的取值范围是（ ）‎ A．‎ ‎1 1‎ ‎[ , )‎ ‎4 2‎ ‎1‎ B．‎ ‎(0, )‎ ‎4‎ ‎1 1‎ C．‎ ‎( , )‎ ‎4 2‎ ‎1‎ D．‎ ‎(0, ]‎ ‎4‎ 二、选择题：本题共 4 小题，每题 5 分，共 20 分。‎ ‎13．若直线ax + 2 y + 6 = 0 与直线 x + a(a +1) y + a2 -1 = 0 垂直，则实数a = ．‎ 14. 若函数 f (x) = lg(ax2 - 2x + 2) 的值域为 R ，则实数a 的取值范围为 ．‎ 15. 四棱锥 P - ABCD 中，底面 ABCD 是边长为 2 的正方形， PA ^ 底面 ABCD ，异面直 线 AC 与 PD 所成的角的余弦值为 10 ，则该四棱锥外接球的表面 积为 ．‎ ‎5‎ ‎16．已知 f (x) = 3x -1 +1 ，若关于 x 的方程[ f (x)]2 - (2 + a) f (x) + 2a = 0 有三个实根，则 实数a 的取值范围为 ．‎ 三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。‎ ‎17．（10 分）已知集合 A = {x |‎ ‎3‎ ‎6 - x ³ 1}， B = {x | x 2 - 11x + 18 < 0} .‎ （1） 求CR ( A Ç B) ， (CR A) Ç B ；‎ （2） 已知C = {x a < x < 2a + 1}，若C Í B ，求实数a 的取值集合．‎ ‎18.（12 分）已知圆C : (x - a)2 + ( y - 2)2 = 4(a > 0) 及直线l : x - y + 3 = 0 ，当直线l 被圆C ‎2‎ 截得的弦长为2 时.‎ （1） 求a 的值；‎ （2） 求过点(3, 5) 并与圆C 相切的切线方程．‎ ‎19.（12 分）如图，在三棱柱 ABC - A1B1C1 中， DABC 是等边三角形， AA1 ^ 平面 ABC ， AA1 = 3AB ， E 是CC1 的中点， F 是 AB 的中点.‎ （1） 求证： CF // 平面 AEB1 ；‎ （2） 求证：平面 AEB1 ^ 平面 AA1B1B ；‎ （3） 若 AA1 = 3 ，求三棱锥 E - AB1B 的体积.‎ ‎20.（12 分）如图，在三棱锥 P - ABC 中， D, E 分别为 AB, PB 的中点，且 ED ^ AB ，‎ PA ^ AC ， PC ^ BC .‎ （1） 求证： BC ^ 平面 PAC ；‎ （2） 若 PA = 2BC 且 AB = EA ，三棱锥 P - ABC 的体积为1，求点 B 到平面 DCE 的距离.‎ ‎21．（12 分）已知幂函数 f (x) = (m2 - 2m +1) xm2 -4m+2 在(0, +¥) 上单调递增；‎ （1） 求m 的值并写出 f (x) 的解析式；‎ （2） 试判断是否存在 a > 0 ，使得函数 g(x) = (2a -1)x - af (x) +1 在[-1, 2] 上的值域为 é-4, 17 ù ？若存在，求出实数 a 的值；若不存在，请说明理由．‎ ê 8 úû ‎22.（12 分）已知函数 f (x) = 1- （1） 求a 的值；‎ （2） 求函数 f (x) 的值域；‎ ‎‎ ‎4‎ ‎2ax + a ‎(a > 0且a ¹ 1) 是定义在(-¥, +¥) 上的奇函数.‎ （1） 当 x Î(0,1] 时， t × f ( x) ³ 2x - 2 恒成立，求实数t 的取值范围． ‎ 数学试卷答案 ‎1-12 ABDBD BADCC CB ‎13、 14、 15、 16、‎ ‎17．解：（1）由题意得，，‎ ‎，又 ‎………………………………5分 ‎（2）当时，得，所以 当时，，所以，综上所述：．………………………………10分 ‎18．解：（1）依题意可得圆心，半径，‎ 则圆心到直线的距离，‎ 由勾股定理可知，代入化简得，‎ 解得或，又，所以；……………………………6分 ‎（2）由（1）知圆，圆心坐标为，圆的半径 由到圆心的距离为，得到在圆外，‎ ‎∴①当切线方程的斜率存在时，设方程为 由圆心到切线的距离，‎ 化简得：，可解得，∴切线方程为；……………………………10分 ‎②当过斜率不存在直线方程为与圆相切．‎ 由①②可知切线方程为或．……………………12分 ‎19．解：（1）取的中点为，连接，因为分别为的中点，‎ 所以，且，‎ 所以且，则四边形为平行四边形，所以，‎ 又面，面，所以面；………………………………4分 ‎（2）因为平面，面，所以，‎ 又为正三角形，为的中点，所以，‎ 又，所以面，又，‎ 所以面，‎ 又面，所以平面平面.…………………………8分 ‎（3）由，得，，又，‎ ‎，即到平面的距离为，得 ‎，故三棱锥的体积为.………………………………6分 ‎20．解：（1）因为为中点，为中点，则，‎ ‎，，又，‎ 又，面，面，‎ 所以面，∵面，∴，‎ 因为，且，面，面，‎ 所以面.………………………………5分 ‎（2）设，设点到平面的距离为.‎ 因为且，所以.‎ 因为，分别为，的中点，所以 因为，所以，，‎ 三棱锥的体积为，得………………………………8分 由（1）知，面，且，所以面 因为，所以，而， ，‎ 且，所以，故 所以，故点到平面的距离为………………………………12分 ‎21．解：（1）是幂函数，，解得：或 而在上递增，故，‎ 故………………………………4分 ‎（2）由（1），‎ 因为，所以图像开口向下，对称轴为，‎ 当，即时，由，得出无解………………………………8分 当，即时，由，解得或（舍去）‎ 经检验当时，，符合题意。‎ 所以存在，使得函数在上的值域为．………………………………12分 ‎22．解：（1）是定义在上的奇函数，即恒成立，‎ ‎，即，解得……………………4分 ‎（2），，由知，‎ ‎，即的值域为………………………………8分 ‎（3）不等式即为，‎ 即：‎ 设，，‎ 时，恒成立 ‎，解得 故的取值范围是………………………………12分