湖北省闻一多中学2011年高中二年级数学必修（Ⅲ）综合测试 7页

闻一多中学2011年高中二年级数学必修3综合测试题（一）‎ 一、选择题 ‎1．在用样本频率估计总体分布的过程中，下列说法正确的是 Ａ．总体容量越大，估计越精确 Ｂ．总体容量越小，估计越精确 Ｃ．样本容量越大，估计越精确 Ｄ．样本容量越小，估计越精确 ‎2．刻画数据的离散程度的度量，下列说法正确的是 ‎（1） 应充分利用所得的数据，以便提供更确切的信息；‎ （2） 可以用多个数值来刻画数据的离散程度；‎ （3） 对于不同的数据集,其离散程度大时，该数值应越小。‎ ‎ A ．(1)和(3) B．(2)和(3) C． (1)和(2) D．都正确 ‎３．数据5，7，7，8，10，11的标准差是 A．8 B．‎4 C．2 D．1‎ ‎４．某公司现有职员160人，中级管理人员30人，高级管理人员10人，要从其中抽取20个人进行身体健康检查，如果采用分层抽样的方法，则职员、中级管理人员和高级管理人员各应该抽取多少人 A．8，15，7 B．16，2，2‎ C．16，3，1 D．12，3，5‎ ‎5．阅读右面的流程图，若输入的a、b、c分别 是21、32、75，则输出的a、b、c分别是：‎ A．75、21、32 B．21、32、75‎ C．32、21、75 D．75、32、21‎ if A ‎ then B else C ‎6．已知两组样本数据的平均数为h，的平均数为k, 则把两组数据合并成一组以后，这组样本的平均数为 A． B． C． D．‎ ‎7．条件语句的一般形式如右所示，其中B表示的是 A．条件 B．条件语句 ‎ ‎ C．满足条件时执行的内容 D．不满足条件时执行的内容 ‎8．从一批产品中取出三件，设A=“三件产品全不是次品”，B=“三件产品全是次品”，C=“三件产品不全是次品”，则下列结论正确的是 A．A与C互斥 B．B与C互斥 C．任两个均互斥 D．任两个均不互斥 ‎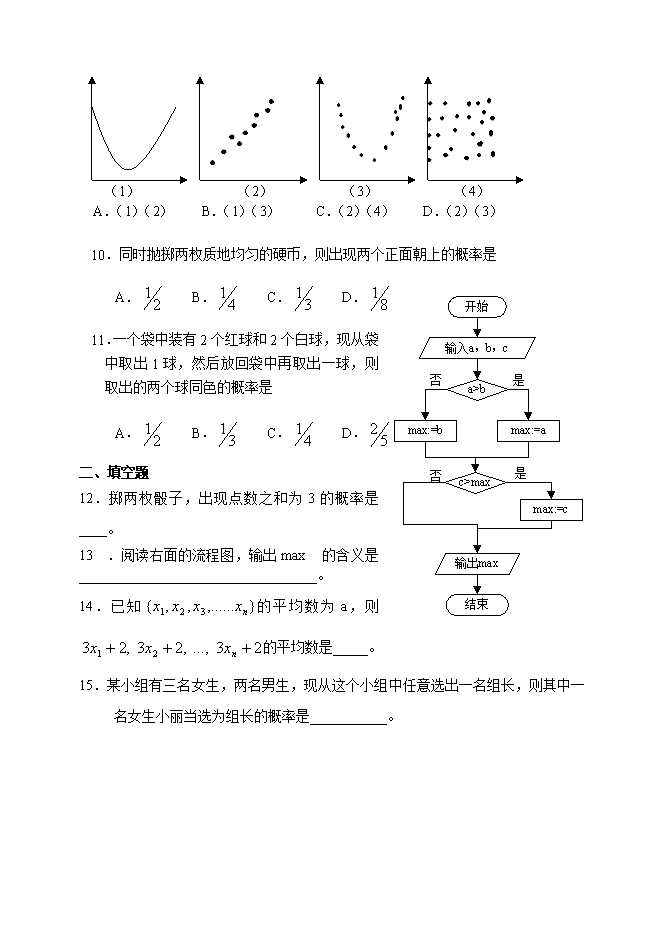9．在下列各图中，每个图的两个变量具有相关关系的图是 ‎ ‎ ‎ （1） （2） （3） （4）‎ A．（1）（2） B．（1）（3） 　 C．（2）（4） D．（2）（3）‎ ‎10．同时抛掷两枚质地均匀的硬币，则出现两个正面朝上的概率是 ‎ A． B． C． D．‎ ‎11．一个袋中装有2个红球和2个白球，现从袋中取出1球，然后放回袋中再取出一球，则取出的两个球同色的概率是 ‎ A． B． C． D．‎ 二、填空题 ‎12．掷两枚骰子，出现点数之和为3的概率是____。‎ ‎13．阅读右面的流程图，输出max的含义是__________________________________。‎ ‎14．已知的平均数为a，则的平均数是_____。‎ ‎15．某小组有三名女生，两名男生，现从这个小组中任意选出一名组长，则其中一名女生小丽当选为组长的概率是___________。‎ 三、解答题 ‎16．有一个容量为100的样本，数据的分组及各组的频数如下：（1）列出样本的频率分布表；（2）画出频率分布直方图和频率折线图。‎ ‎17．设计算法流程图，要求输入自变量的值，输出函数的值，并用复合if语句描述算法。‎ ‎18．已知，设计算法流程图，输出。‎ ‎19．甲盒中有一个红色球，两个白色球，这3个球除颜色外完全相同，有放回地连续抽取2个，每次从中任意地取出1个球，用列表的方法列出所有可能结果，计算下列事件的概率。‎ ‎（1）取出的2个球都是白球； （2）取出的2个球中至少有1个白球。‎ 闻一多中学2011年高中二年级数学必修（Ⅲ）综合测试题（一）参考答案：‎ 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ 答案 C C C C A B C B D B A 二、填空题 ‎12．掷两枚骰子，出现点数之和为3的概率是1/18。‎ ‎13．阅读右面的流程图，输出max的含义是a、b、c中的最大值。‎ ‎14．已知的平均数为a，则的平均数是‎3a+2。‎ ‎15．某小组有三名女生，两名男生，现从这个小组中任意选出一名组长，则其中一名女生小丽当选为组长的概率是1/5。‎ 三、解答题 ‎（1）样本的频率分布表；‎ 分组 频数 频率 ‎6‎ ‎0.06‎ ‎0.02‎ ‎16‎ ‎0.16‎ ‎0.053‎ ‎18‎ ‎0.18‎ ‎0.06‎ ‎22‎ ‎0.22‎ ‎0.073‎ ‎20‎ ‎0.20‎ ‎0.067‎ ‎10‎ ‎0.10‎ ‎0.033‎ ‎8‎ ‎0.08‎ ‎0.027‎ ‎ 频率/组距 ‎ 0.073‎ ‎ ‎ ‎ 0.020‎ ‎ ‎ ‎ 12.5 15.5 18.5 21.5 24.5 27.5 30.5 33.5 ‎ 频率折线图略.‎ ‎17． 18.‎ 输入；‎ if x < 0， 19.解略(1) (2) ‎ then f(x):= π/2∙x+3；‎ else if x = 0， ‎ then f(x):=0；‎ ‎ else f(x):= π/2∙x-5. 输出f(x).‎