高中数学好题速递400题（201—250） 27页

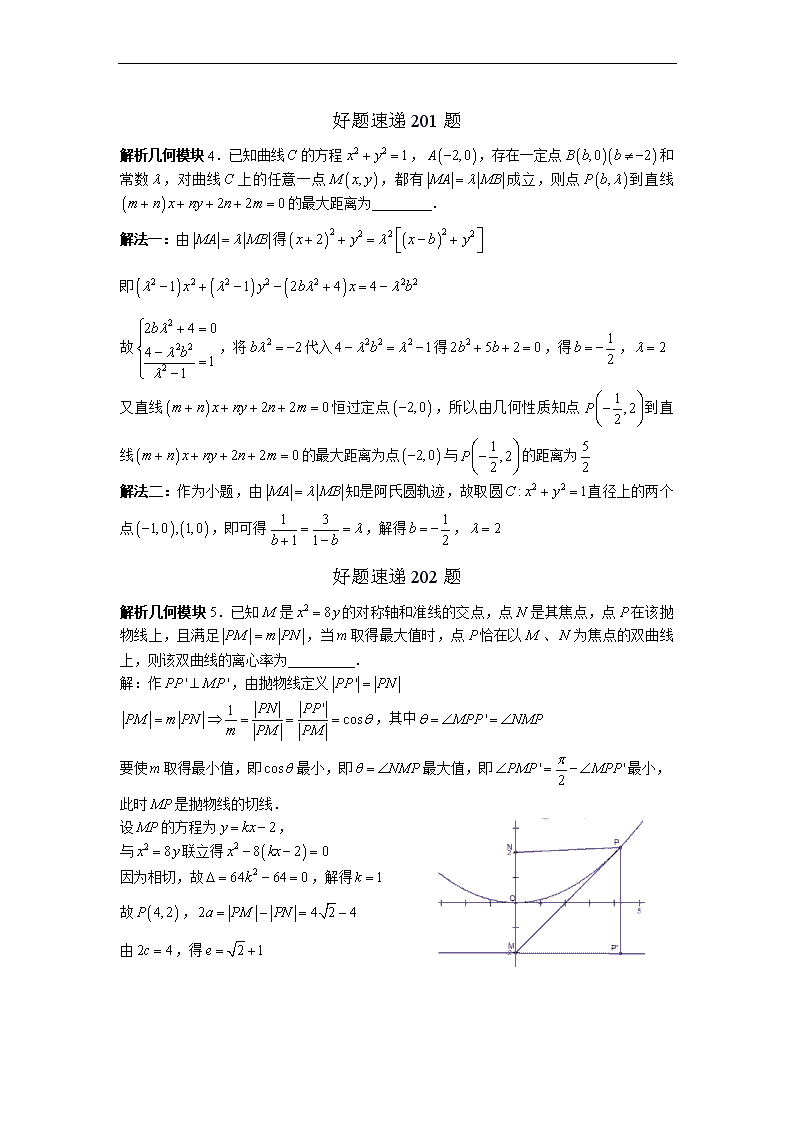
好题速递201题 解析几何模块4．已知曲线的方程，，存在一定点和常数，对曲线上的任意一点，都有成立，则点到直线的最大距离为 ．‎ 解法一：由得 即 故，将代入得，得，‎ 又直线恒过定点，所以由几何性质知点到直线的最大距离为点与的距离为 解法二：作为小题，由知是阿氏圆轨迹，故取圆直径上的两个点，即可得，解得，‎ 好题速递202题 解析几何模块5．已知是的对称轴和准线的交点，点是其焦点，点在该抛物线上，且满足，当取得最大值时，点恰在以、为焦点的双曲线上，则该双曲线的离心率为 ．‎ 解：作，由抛物线定义 ‎，其中 要使取得最小值，即最小，即最大值，即最小，此时是抛物线的切线．‎ 设的方程为，‎ 与联立得 因为相切，故，解得 故，‎ 由，得 好题速递203题 解析几何模块6． 已知斜率为1的直线过双曲线的左焦点，且与双曲线左、右支分别交于两点，若是线段的中点，则双曲线的离心率为 ．‎ 解：由题意知 所以，所以 好题速递204题 解析几何模块7． 已知点是双曲线上的动点，是其左、右焦点，坐标原点，若的最大值是，则此双曲线的离心率是 ．‎ ‎ 解：设，则 又，所以 所以 所以 所以的最大值在时取到，所以 所以，即 好题速递205题 解析几何模块8．在平面直角坐标系中，圆的方程为，直线与圆相交于两点，为弦上一动点，以为圆心，2为半径的圆与圆总有公共点，则实数的取值范围是 ．‎ 解：两圆有公共点的充要条件是，而恒成立，故只要时两圆必有公共点．由平面几何知识可知，为点到直线的距离，所以，解得 好题速递206题 解析几何模块9．已知点，，若圆上存在一点，使得，则的最大值为 ．‎ 解：由得在以中点为圆心，为半径的圆上，所以的轨迹方程为，所以圆的半径为，又由在圆上，的圆心，半径为1，当圆与圆内切时，最大为 好题速递207题 立体几何模块1．如图，在正方体中，是棱的中点，是侧面上的动点，并且平面，则动点的轨迹是（ ）‎ A．圆 B．椭圆 C．抛物线 D．线段 ‎ 解：如图，取的中点，的中点，显然可证明平面平面，当在线段上时，均有平面 ‎，即动点的轨迹是线段。‎ 点评：善于转化是解决立体几何中平行与垂直问题的关键。例如，考虑“线线平行”时，可转化为“线面平行”或“面面平行”；考虑“线面平行”时，可转化为“线线平行”或“面面平行”；考虑“面面平行”时，可转化为“线线平行”或“线面平行”。‎ 在斜二测画法画图时，平行关系不会改变，因为要找平行线，可以考虑在图象上推平行线，然后关注哪个位置看起来比较特殊，例如中点，中位线之类。‎ 好题速递208题 立体几何模块2．如图，在三棱柱的侧棱与上各有一个动点，，且满足，是棱上的动点，则的最大值是 ．‎ 解法一：设，则 ‎（注：这里用到了梯形的面积与的面积相等。）‎ 即与重合时，最大，‎ 解法二：设，为定值，则是关于的增函数 所以 好题速递209题 立体几何模块3．已知线段，且与平面的距离为4，点是平面上的动点，且满足，若，则线段长度的取值范围是 ．‎ 解：如图，将线段投影到平面上，得到射影，将空间问题平面化，则动点的轨迹是以为圆心，半径为的圆，‎ 又，，，‎ 所以，即 好题速递210题 立体几何模块4．已知为正方体对角线上的一点，且，下面结论：‎ ‎①；②若平面，则；③若为钝角三角形，则；‎ ‎④若，则为锐角三角形．‎ 其中正确结论的序号为 ．‎ 解：在正方体中，平面，又平面，故，①正确； ‎ 由题可知，若平面，则 设正方体的棱长为1，则，，，在中，‎ 所以，所以，②正确；‎ 在正方体中，以为轴，为轴，为轴建系，设棱长为2，则 设，由，得 所以，，‎ 若为钝角三角形，则为钝角，，解得，③错；‎ 同理，当时，，所以为锐角三角形，④正确。‎ 所以正确结论为①②④。‎ 好题速递211题 立体几何模块5．如图，在棱长为1的正方体中，若点是棱上一点，则满足的点有 个．‎ 解：点既在以为焦点，长轴为2的椭球上，又在正方体的棱上。‎ 因为，故点在以为焦点，长轴为2的椭球外，所以椭球必与线段相交（交点就是的中点），同理在上各有一个交点满足条件 又若点在上，则，故上不存在满足条件的点，同理上也不存在满足条件的点。‎ 好题速递212题 立体几何模块6．将一个长宽分别为的铁皮的四个角切去相同的正方形，然后折成一个无盖的长方体的盒子（不计粘合处），若这个长方体的外接球的面积存在最小值，则的取值范围是 ．‎ 解：设切去的小正方形的边长为，长方体的外接球的半径为 则 因为长方体的外接球的面积存在最小值，所以，解得 好题速递213题 在直角梯形中，，，，，动点在以为圆心且过点的圆内运动（不含边界），设，则的取值范围是 ．‎ 解：建立直角坐标系，， ，，，‎ 由得 动点在内运动，所以 求目标函数的取值范围是 好题速递214题 在曲线上任取两点，则的最小值为 ．‎ 解：记，则 且，，‎ 同时满足，即，‎ 当且仅当时取得“=”，故的最小值为2．‎ 好题速递215题 已知函数是定义在上的不恒为零的偶函数，且对任意实数都有，则 ．‎ 解：令，则，所以 令，则 当时，由得 则，故 好题速递216题 已知实数，设函数的两个零点分别为，则下列关系中恒成立的是（ ）‎ ‎（A） （B）‎ ‎（C） （D）‎ 解：的两个零点，‎ 即的两个零点 因为开口向上，，又，所以 即函数的零点一个大于，一个小于，且，‎ 所以根据“一上一下，中间一点”的原则，可知，选C 好题速递217题 已知点在抛物线上，若的三个顶点都在抛物线上，记三边所在直线的斜率分别为，则 ．‎ 解：，设，‎ 所以 点评：抛物线题目的计算量相对于椭圆、双曲线要小一些，主要是基于抛物线上的点的设法，在化简过程中利用好平方差公式，可以使得计算简便。这个过程要做到比较熟练。‎ 好题速递218题 已知函数与函数在区间上都有零点，则的最小值为 ．‎ 解：由题意知，，两式相加得 ‎，两式相加得 所以 当且仅当时取得等号。‎ 点评：这里用到了基本不等式，如果一下子看不出来，也可以先利用齐次化思想，将分子分母同除以，令，将式子简化，就容易发现了。‎ 好题速递219题 已知函数，若在上既有最大值又有最小值，且最大值与最小值的和为4，则 ．‎ 解：‎ 已知在上既有最大值又有最小值，故 又是奇函数，且最大值与最小值的和为4，则，‎ 故 好题速递220题 对于函数，如果存在区间，同时满足下列条件：①在内是单调的；②当定义域是时，的值域也是，则称是该函数的“和谐区间”．若存在“和谐区间”，则的取值范围是 ．‎ 解：因为在和上是增函数，所以或，且，‎ 因此是方程的两个不相等且同号的实数根，即有两个不相等且同号的实数根 又且，故只需，解得 又，故 好题速递221题 已知以为周期的函数，其中，若恰有5个实数解，则的取值范围是 ．‎ 解：当时，原函数式化为方程，表示一个半椭圆，当时，是两线段和组成的折线，再根据周期性画出大致图象如图所示。‎ 由图象可知，当直线与第二个半椭圆相交，而与第三个半椭圆无交点时，方程恰有5个实数解，‎ 由方程组消去得 由，解得 由方程组消去得 由，解得，所以 好题速递222题 ‎（2015重庆理科第16题）若函数的最小值为5，则 ________．‎ 解法一：按照两类分类讨论，画出的折线图，图象最低点的纵坐标为5，求得或 解法二：由题意得，从而 设 的图象是以为顶点的开口向上的“V”形图。‎ 的图象是以为顶点的开口向下（开口比的图象开口大）的“V”形图，且与轴交点的坐标为。‎ 当或时，，所以若函数的最小值为5，则或 好题速递223题 若动点在直线上，动点在直线上，设线段的中点为，且，则的取值范围是________．‎ 解法一：设点满足，点满足 两式相加得点的轨迹是直线 同时点满足 所以满足条件的点在线段上，其中点，分别为直线与圆的交点，表示线段上的点与坐标原点连线距离的平方，所以当运动到或时，取得最大值为16，当运动到圆心时，取得最小值为8，故 解法二：将代入，得到 将代入得 好题速递224题 ‎★设反比例函数与二次函数的图象有且仅有两个不同的公共点，，且，则 ．‎ 解：与的图象有且仅有两个不同的公共点 方程有两个不同的实数根 方程有两个不同的实数根 三次方程仅有两个实根，故必有一个是一次根，一个是重根。‎ 方程或 对于第一种情况，等式两边展开比较系数得，，‎ 故，因为，所以，‎ 对于第二种情况，等式两边展开比较系数得，，‎ 故，因为，所以，但由知，与矛盾，故舍去。‎ 点评：本题是自山东高考题改编而来，解法中运用了三次方程求根的因式分解，奇次根穿过与偶次根反弹的问题。浙江高考曾多次考过类似的问题，值得注意。例如：‎ ‎（2014浙江文7）已知函数，且，则 A． B． C． D．‎ 解：方程的三个根为，‎ 故 比较系数得，故 ‎（2012浙江理17）设，若时均有，则____．‎ 解：，且，因为对恒成立，则必是二重零点 ‎ 代入得：，解之得：，舍去，得答案：‎ ‎（2013浙江文16）设，若时恒有，则 。‎ ‎【解析】当时，有，所以得，代回原式 故必定是重根，即中必有因子，所以，所以 点评：这三道题都是加深零点意义理解的好题。零点就像是x轴上的守门员，关系着函数正负性变化的重任，“奇重零点穿过，偶重零点反弹”。‎ 好题速递225题 设是正实数，且，则的最小值是________．‎ 解：设，，则题目变为“已知，求的最小值。‎ 当且仅当，即，即时取得等号 点评：本题还是分母换元使得式子简化，灵活运用均值不等式。‎ 好题速递226题 ‎（重庆高考题）函数的值域是__________．‎ 解：‎ 设，则问题变为求的值域 解法一：当时，有 将视为圆上任一点与原点连线的斜率，结合图形可知，‎ 所以，‎ 当时，‎ 综上可知，‎ 解法二：注意到，联想其结构特征与三角函数中的正余弦定义式相似 于是设直线的倾斜角为，则 所以 好题速递227题 已知，，，，则的取值范围是________．‎ 解法一：考虑向量模的几何意义 由和，可作出图形 的终点必在以为直径的圆上 又，故的终点必在以为圆心，1为半径的圆上 所以问题转化为与（半径为1的小圆）有交点 注意到的半径为，圆心距 所以两圆相交需满足 且有 作一个整体换元，设，‎ 问题转化为规划问题，已知，求的取值范围。‎ 如图可得 解法二：代数方法 ‎，因此只需求的取值范围 由得 所以 即，解得 所以，故 解法三：解析几何坐标方法 解：设，设A，B是以O为圆心，2为半径的圆上两点，且AC^BC，则 | a－b | = AB = 2 MC．‎ ‎∵MO2 + MA2 = OA2，而MA = MC，∴MO2 + MC2 = 4．‎ 设，则，‎ 即．（*）‎ ‎| a－b | = AB = 2 MC = ．‎ 由（*）知，，‎ ‎∴，即．‎ ‎∴．‎ 好题速递228题 已知实数，满足，，则的最大值是________．‎ 解：记，则 因为 故 即的最大值是 好题速递229题 设函数，，若对任意的，总存在，使得成立，则实数的取值范围是________．‎ 解法一：由题意知的值域是值域的子集，易得的值域是 设，则的值域为的值域，再通过分类讨论进行解答 或或或 解得 解法二：解法一常规，但计算量较大，作为填空题不划算。故从数形结合的角度，利用函数图象给出解法二。‎ 的值域是，设，‎ 则问题可以转化为对任意实数，关于的方程在上有解，‎ 即对任意实数，总存在，使得直线与在是有公共点，‎ 即直线与一簇函数个个都有公共点，‎ 从图象上显然看到，只要直线与函数有公共点即可，于是求得 好题速递230题 在中，边上的中线，若动点满足，则的最小值是 ．‎ 解：因为，系数之和为1，故三点共线，且，所以点在线段上，设，‎ 故 当时，取最小值 好题速递231题 设数列满足，且，则 ．‎ 解：找规律。易知，，，，，……，‎ 故数列是周期为5的数列，所以 好题速递232题 设数列满足，且，则 ．‎ 解：‎ 即 令，则，即数列是等比数列，且，故，即 好题速递233题 已知，函数的零点分别为，函数的零点分别为，则的最小值为 ．‎ 解：‎ 由（1）（2）得 因为，故 好题速递234题 已知函数，其中，设为的一个零点，若，则符合条件的的值有 个．‎ 解：‎ 因为，故，解得 由知，‎ 当时，；当时，；当时，（舍去）；当时，‎ 综上，符合条件的或，有两个值。‎ 好题速递235题 已知是的外心，，，，若，则的最小值为 ．‎ 解：因为，‎ 解得 ，‎ 故 点评：这里又是三角形外心与向量的常见结合题，“外心点积转边投影”是正道。‎ 好题速递236题 ‎★已知函数，设，，若函数有四个零点，则的取值范围是 ．‎ 解：是开口形状确定，顶点在上运动的抛物线，于是当取不同值时所对应的函数图象如图所示，是“W型”的图象 交点横坐标由解得 函数有四个零点，可视为直线与函数有四个交点，故只需两条抛物线的“交叉点”到直线的竖直距离大于即可。‎ 故，解得 好题速递237题 在中，若，，则的面积取得最大值时，最长的边长等于 ．‎ 解法一：设，，‎ 由题知，，‎ 因为 故，当且仅当时，取得最大值，此时 解法二：由余弦定理知 故 当且仅当时，等号成立，故最长边为 好题速递238题 如图，在半径为1的上，线段是的直径，则的取值范围是 ．‎ 解法一：极化恒等式角度 显然当均为的直径时，最大为4；‎ 取的中点，则由极化恒等式知 故 解法二：投影角度 要求，显然在确定的情况下，最大。‎ 如图，当且与圆相切时，最大。‎ 此时设，则，‎ 所以 显然当且仅当与重合，与重合，即与反向且模长均为直径时，‎ 解法三：坐标角度 设，‎ 所以 令 则 令 则（当且仅当时取得等号）‎ 解法四：利用竞赛知识 设，，‎ 则 在竞赛中证明过一个不等式，在中，有 所以 这里用了三角的积化和差、和差化积公式，属于超纲内容。‎ 所以 好题速递239题 ‎★在平面直角坐标系中，设是圆上不同的三个点，若存在实数，使得，则的取值范围是 ．‎ 解法一：‎ ‎（这里的就是向量夹角，由于三点不同，故）‎ 当时有 当时有 画出可行域如图，‎ 于是将视为可行域内的到点 的距离的平方，易得当时，，当时，，故 解法二：‎ 于是 解法三：由可以构造三角形法则 故设，则构成的三边（否则三点中至少有两个点重合），如图所示 于是满足，画出可行域，后续如解法一。‎ 好题速递240题 ‎★已知二次函数为非负，则的最小值为 ．‎ 解法一：齐次化思想 根据条件有，则 因此 令，则 当且仅当及时取得最小值，即时取得。‎ 解法二：根据条件有，则 故 令得 当且仅当及时取得最小值，即时取得。‎ 解法三：令，得，代入 得 当且仅当时取得等号 解法四：待定系数法 假设，化简为 又 故比对系数得，得，即，此时 即因为，所以 因为，所以 好题速递241题 已知，，则的最大值是 ．‎ 解法一：判别式法 令，代入得 关于的一元二次方程有解得，即 所以，当且仅当时取得等号。‎ 解法二：化齐次式 令 故 当且仅当时取得等号。‎ 解法三：‎ 令，即 设，则 故 解法四：利用余弦定理构造三角形 设的三边分别为，由得 由正弦定理，故 故 其中，故取，‎ 故 评注：本题是很常见的最值问题，解法一、解法二是常规的两种方法，解法三利用三角换元，解法四构造三角形的方法不仅求出了最大值，还取到了最小值。‎ 好题速递242题 ‎（2015全国联赛2）若实数满足，则的值为 ．‎ 解：由得，‎ 评注：这里用了1的逆用，简化了计算，当然也可以把都算出来，不过计算量比较大。‎ 好题速递243题 ‎（2015全国联赛4）在矩形中，，边上（包含）的动点与的延长线上（包含点）的动点满足，则的最小值为 ．‎ 解：不妨设，则，则由得，‎ 故 评注：坐标法解决向量问题是常见方法。‎ 好题速递244题 ‎（2015全国联赛6）在平面直角坐标系中，点集所对应的平面区域的面积为 ．‎ 解：设 先考虑在第一象限中的部分，此时有，故这些点对应于图中的及其内部，由对称性知，对应的区域是图中以原点为中心的菱形及其内部 同理设，则对应的区域是图中以为中心的菱形及其内部。‎ 由点集的定义知，所对应的平面区域是被，中恰好一个所覆盖的部分，因此本题所要求的即为图中阴影区域的面积 由直线，直线得交点 由对称性知，‎ 好题速递245题 ‎（2015全国联赛7）设为正实数，若存在，使得，则的取值范围是 ．‎ 解：由知，‎ 而，故题目条件等价于：‎ 存在整数，使得 ①‎ 当时，区间的长度不小于，故必存在满足①式 当时，注意到，故仅需要考虑如下几种情况：‎ ‎（i），此时且，无解 ‎（ii），此时 ‎（iii），此时，得 综上，可知或 好题速递246题 ‎（2015全国联赛9）若实数满足，，则的最小值是 ．‎ 解：设，则 由条件知，‎ 故 故 当且仅当，即，的最小值为 由于，故的最小值为 评注：本题又是“三个字母两个方程，少一个合情合理”的问题。在处理的时候用到了三元均值不等式 好题速递247题 ‎（2015安徽全国联赛3）设平面向量满足，则的取值范围是 ．‎ 解法一：由于，当时取得等号 又，当时取得等号 故 解法二：取平面内，，则 于是问题转化为在同心圆环（）内的两点之间的距离在之间，求的取值范围。‎ ‎（评注：又是一个点发出的两个向量做点积，极化恒等式又有用武之地啦！）‎ ‎，其中是线段的中点 如图所示，由圆的垂径定理得，‎ 当位于半径为3的圆周上，且时取得最大值为 当重合时，取得最小值为0‎ 所以 因此，即，即 好题速递248题 A B C P H O 在平面直角坐标系中，已知点在圆内，动直线过点且交圆于两点，若面积的最大值为16，则实数的取值范围是 ．‎ 解：‎ ‎，‎ 故 故面积的最大值为16，即能取得4。‎ 由图象可知，，故 解不等式得或 好题速递249题 如图，已知边长为1的正的顶点在平面内，顶点在平面外的同一侧，点分别为在平面内的投影，设，直线与平面所成的角为。若是以角为直角的直角三角形，则的取值范围是 ．‎ 解法一：如图建系，设，，则 因为且，故 又因为，故，又，故 又因为，，故 解法二：注意到 考虑为直线与 平面所成的角，显然其上界（无法取得）为，此时；其最小值当时取得，为，因此所求的范围为 好题速递250题 在中，边上的中垂线分别交于，若，，则 ．‎ 解：取作为基底向量，则，‎ 设 由得，即 ①‎ 而得，整理得 ②‎ 将①式代入②式得，故