MidasCivil桥梁抗震详解 117页

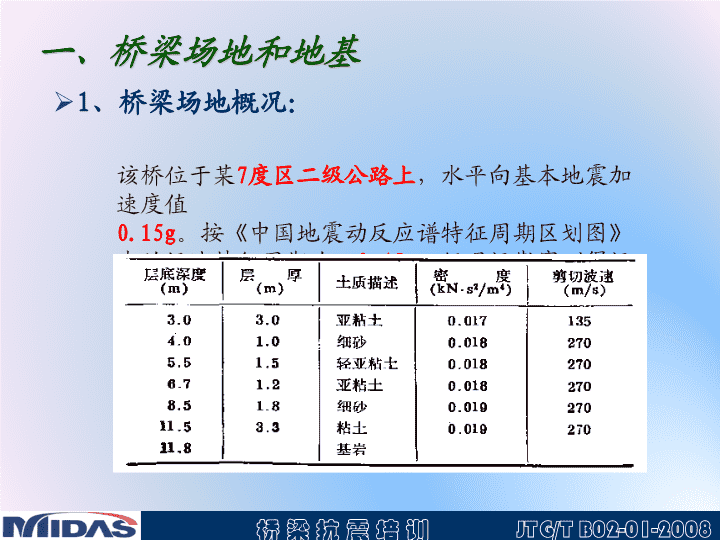
新规范桥梁抗震设计详解 桥 梁 抗 震 培 训 JTG/T B02-01-2008 该桥位于某 7 度区二级公路上 ，水平向基本地震加速度值 0.15g 。按 《 中国地震动反应谱特征周期区划图 》 查的场地特征周期为： 0.45s 。经现场勘察测得场地土质和剪切波速如下： 一、桥梁场地和地基 桥 梁 抗 震 培 训 JTG/T B02-01-2008 1 、桥梁场地概况： 2 、 场地类别确定 ： 土层平均剪切波速为： 209.8m/s 桥 梁 抗 震 培 训 JTG/T B02-01-2008 a 、确定土层平均剪切波速： 一、桥梁场地和地基 按此条规范确认为： 11.5m 。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 2 、 场地类别确定 ： b 、确定工程场地覆盖层厚度： 一、桥梁场地和地基 查得场地类别为 Ⅱ 类 场地 桥 梁 抗 震 培 训 JTG/T B02-01-2008 2 、 场地类别确定 ： 一、桥梁场地和地基 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、地基抗震验算： 一、桥梁场地和地基 根据土质判断是否需要抗液化措施： 判别地基不液化，不需进行抗液化措施。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4 、液化判别： 一、桥梁场地和地基 二、桥梁构造、材料概况 桥梁形式： 三跨混凝土悬臂梁 桥梁长度： L = 30+ 50 +30 = 110.0 m ，其中中跨为挂孔结构，挂孔梁为普通钢筋混凝土梁，梁长 16m ，墩为钢筋混凝土双柱桥墩， 墩高 9m 预应力布置形式： T 构部分配置顶板预应力，边跨配置底板预应力 跨中箱梁截面 墩顶箱梁截面 桥 梁 抗 震 培 训 JTG/T B02-01-2008 二、桥梁构造、材料概况 桥 梁 抗 震 培 训 JTG/T B02-01-2008 材料 混凝土 主梁采用 JTG04 （ RC ）规范的 C50 混凝土 桥墩采用 JTG04 （ RC ）规范的 C40 混凝土 钢材 采用 JTG04 （ S ）规范，在数据库中选 Strand1860 荷载 恒荷载 自重，在程序中按自重输入，由程序自动计算 二、桥梁构造、材料概况 桥 梁 抗 震 培 训 JTG/T B02-01-2008 预应力 钢束 (φ15.2 mm×31) 截面面积 : Au = 4340 mm 2 孔道直径 : 130 mm 钢筋松弛系数 ( 开 ), 选择 JTG04 和 0.3( 低松弛 ) 超张拉 ( 开 ) 预应力钢筋抗拉强度标准值 (fpk):1860N/mm^2 预应力钢筋与管道壁的摩擦系数 :0.25 管道每米局部偏差对摩擦的影响系数 :1.5e-006(1/mm) 锚具变形、钢筋回缩和接缝压缩值 : 开始点 :6mm 结束点 :6mm 张拉力 : 抗拉强度标准值的 75% ，张拉控制应力 1395MPa 二、桥梁构造、材料概况 桥 梁 抗 震 培 训 JTG/T B02-01-2008 三、基本参数确定 1 、确定桥梁抗震设防类别： 二级公路大桥，故该桥为 B 类 桥梁。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 2 、确定抗震设防等级： 在 7 度区，按 8 度构造 措施设防 三、基本参数确定 桥 梁 抗 震 培 训 JTG/T B02-01-2008 桥 梁 抗 震 培 训 JTG/T B02-01-2008 抗震设计总流程 E1 地震作用下抗震分析步骤 桥 梁 抗 震 培 训 JTG/T B02-01-2008 1 、确定桥梁类型： 确定为规则桥梁 桥 梁 抗 震 培 训 JTG/T B02-01-2008 2 、确定分析方法： 采用 MM 法。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 E1 地震反应谱的确定： a 、确定重要性系数 ： 得该桥在 E1 地震作用下重要性系数为 ，在 E2 地震作用下重要性系数为 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 E1 地震反应谱的确定： b 、确定场地系数 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 E1 地震反应谱的确定： c 、确定设计基本地震动加速度峰值 A ： 在设防烈度 7 度区， A 值为 0.15g 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 E1 地震反应谱的确定： d 、调整设计加速度反应谱特征周期 调整后为 ： 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 E1 地震反应谱的确定： e 、对阻尼比为 0.05 的标准反应谱进行修正 阻尼比为： 0.05 ，计算阻尼调整系数得 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 E1 地震反应谱的确定： f 、生成反应谱 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 E1 地震反应谱的确定： 与静力分析模型的区别：不在精细地模拟，而重点是要真实、准确地反映结构质量、结构及构件刚度、结构阻尼及边界条件。 ---- 参见规范 6.3 模 型 质量 刚度 阻尼 边界条件 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4 、 空间动力分析模型的建立 ： 质量： 将建立的模型进行质量转换。集中质量法：一般梁桥选择，计算省时，不能考虑扭转振型。一致质量法：通用，耗时，可以考虑扭转振型。 路灯质量转换 将二期等反映铺装的荷载转换成质量。 对于没用荷载表示的附属构件，如路灯等，可在节点上施加相应的质量块。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 ---- 参见规范 6.3 4 、 空间动力分析模型的建立 ： 刚度： 构件刚度在地震往复作用下一般会降低，理论上应使用各个构件的相对动刚度，但选择静刚度满足工程要求。 阻尼： 一般使用阻尼比 来反应整个桥梁的全部阻尼。 1 、钢筋混凝土、预应力钢筋混凝土梁桥阻尼比一般选择 2 、钢桥阻尼比一般选择 3 、钢混结合梁桥分别定义钢构件组组阻尼比 、混凝土构件组组阻尼比 ，程序计算各阶振型阻尼比： 4 、钢混叠合梁桥可使用介于 0.02-0.05 之间的阻尼比如： 桥 梁 抗 震 培 训 JTG/T B02-01-2008 ---- 参见规范 6.3 4 、 空间动力分析模型的建立 ： 边界条件： 各个连接构件（支座、伸缩缝）及地基刚度的正确模拟。 连接构件： 普通板式橡胶支座：弹性连接输入刚度。 固定盆式支座：主从约束或弹性连接。 活动盆式支座：理想弹塑性连接单元。 摩擦摆隔震支座、钢阻尼器、液体阻 尼器：程序专门的模拟单元 。 预应力拉索：一般连接－钩单元。 伸缩缝和橡胶挡块：一般连接－间隙 单元。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 ---- 参见规范 6.3 4 、 空间动力分析模型的建立 ： 地基刚度的模拟： 在墩低加上弹簧支承，算出各个方向上的弹簧刚度。 真实模拟桩基础，利用土弹簧准确模拟土对桩的水平侧向力、竖向摩阻力。一般可用表征土介质弹性的“ M ”法 。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 ---- 参见规范 6.3 4 、 空间动力分析模型的建立 ： 桥梁参与组合计算的振型阶数的确定 两种方法确定结构自振特性：特征值求解和利兹向量求解。 为了快速满足规范 6.4.3 ，经常会用利兹向量法来计算参与组合计算的振型。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 a 、 自振特性分析 ： SRSS 法和 CQC 法 ： 根据规范 6.4.3 ，有 SRSS 法和 CQC 法以供选择。 当结构振型分布密集，互有耦联时，推荐用 CQC 。 b 、振型 组合方法的确定 桥 梁 抗 震 培 训 JTG/T B02-01-2008 根据规范 5.1.1 ，该直线桥只需考虑顺桥向 X 和横桥向 Y 的地震作用。 c 、地震作用分量组合的确定 桥 梁 抗 震 培 训 JTG/T B02-01-2008 桥台 高 4 ， 台背宽 10 ，侧宽 3 ，土 的容重 为 ， 土的内摩擦角为： 根据 规范 5.5.2 ，土压力分布力 ，本例转化成 集中力台背为： 412 。侧向为： 124 d 、地震主动土压力 桥 梁 抗 震 培 训 JTG/T B02-01-2008 一般冲刷线算起的水深为： 5m 。 水的容重为： ， 根据规范 5.5.3 ，地震动水压力为 0.92kN e 、地震 动水压力 桥 梁 抗 震 培 训 JTG/T B02-01-2008 按现行的公路桥涵设计规范相应的规范验算桥墩强度。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5 、 强度验算 ： E2 地震作用下抗震分析步骤 MM 桥 梁 抗 震 培 训 JTG/T B02-01-2008 1 、确定分析方法： 采用 MM 法或 NTH 法。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 2 、 E2 反应谱的确定 步骤与 E1 反应谱的确定相同，但需注意 重要性系数 的取值不同，其他参数相同，得 E2 地震作用下反应谱如下。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 一、选用实录地震波并进行适当调整 a.midas Civil 中提供了近 40 种实录地震波 b. 用户定义 c. 导入 二、人工地震波 a 、相关部门提供的人工地震波； b 、 clan 和 Sacks 在 1974 年提出的用三角级数叠加来模拟地震动加速度； 地震波的来源 本例中主要选择实录地震波。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 地震波的三要素 地震动三要素： 频谱特性、有效峰值和持续时间。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 按反应谱面积控制 先计算 EPA 、 EPV ，据此计算 并比较 调取实录 地震波 持时判断 峰值判断 是 否 否 是 是 是 否 与设计反应谱分析结果比较 , 双指标控制 选用 是 桥 梁 抗 震 培 训 JTG/T B02-01-2008 否 3 、 设计加速度时程的确定（选用实录波） 一般用加速度幅值调整 地震动幅值包括加速度、速度和位移的峰值、最大值或者某种意义上的有效值。加速度峰值 PGA 、速度峰值 PGV 和位移峰值 PGD 是地面运动强烈程度最直观的描述参数。加速度峰值是最早提出来的、也是最直观的地震动幅值定义。 幅值的种类 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3.1 、幅值的调整 3 、 设计加速度时程的确定（选用实录波） 因为峰值参数并非描述地震动的最理想参数，由高频成分所确定的个别尖锐峰值对结构的影响并不十分显著，所以美国 ATC-30 样本规范所采用的是有效峰值加速度 EPA ，对有效峰值加速度 EPA 的求法参见 《 midas/Civil 2006 桥梁抗震设计功能说明 》 ，而我国 《08 细则 》 采用峰值加速度 PGA 。 美国采用有效加速度峰值 EPA ， 而我国采用的是加速度峰值 PGA 3.1 、幅值的调整 有效加速度峰值 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 以设计加速度反应谱最大值 Smax 除以放大系数（约 2.25 ）得到。 设计加速度峰值 PGA 的求法 E1 地震时程分析所用地震加速度时程曲线的最大值： E2 地震时程分析所用地震加速度时程曲线的最大值： 对于本例： 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3.1 、幅值的调整 3 、 设计加速度时程的确定（选用实录波） 调整加速度曲线 式中： 、 分别是调整后的加速度曲线和峰值； 、 分别是原记录的加速度曲线和峰值； 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3.1 、幅值的调整 3 、 设计加速度时程的确定（选用实录波） 本例选择程序自带实录地震波： 1940, El Centro Site, 270 Deg 进行调整 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3.1 、幅值的调整 3 、 设计加速度时程的确定（选用实录波） 打开工具－地震波数据生成器－ Generate － Earthquake Response Spectra 选择程序自带实录地震波： 1940, El Centro Site, 270 Deg 加速度峰值 PGA 调整系数 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3.1 、幅值的调整 3 、 设计加速度时程的确定（选用实录波） 因为拟相对速度反应谱 PSV 和拟绝对加速度的反应谱 PSA 之间有近似关系： 则可得到特征周期 ： 其中： 为有效峰值加速度 为有效峰值速度。 对选定的实录地震波，首先求 EPV 、 EPA 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3.2 、确定实录波的特征周期 3 、 设计加速度时程的确定（选用实录波） 在 midas 程序中提供将地震波转换为各种长周期谱的功能（工具－地震波数据生成器，生成后保存为 SGS 文件），用户可以利用保存的 SGS 文件（文本格式文件）根据上面所述方法计算 EPV 、 EPA a 、 1978 年美国 ATC-3 规范中的定义求 EPA 、 EPV （频段固定）； b 、 1990 年 《 中国地震烈度区划图 》 求 EPA 、 EPV （频段不固定）； 详细过程参见资料 《 midas/Civil 2006 桥梁抗震设计功能说明 》 3.2 、确定实录波的特征周期 1 、确定 EPV 、 EPA 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 1 、幅值调整为 0.5464 2 、阻尼比输入 0.05 3 、输入长周期到 10 秒 4 、勾选 X 坐标对数化 3.2 、确定实录波的特征周期 2 、求 EPA 3 、 设计加速度时程的确定（选用实录波） 1 、幅值调整为 0.5464 2 、阻尼比输入 0.05 3 、输入长周期到 10 秒 4 、勾选 X 坐标对数化 3.2 、确定实录波的特征周期 3 、求 EPV 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 采用 1978 年美国 ATC-3 规范中的定义求 EPA 、 EPV （频段固定）； 3.2 、确定实录波的特征周期 3 、 设计加速度时程的确定（选用实录波） 该桥址场地特征周期为 0.45s ，与实录波特征周期 0.519 比较接近，故实录波的特征周期符合要求。 3.3 、比较实录波的特征周期与桥址特征周期 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 双指标选波采用两个频段控制：一、对地震记录加速度反应谱值在 平台段的均值进行控制，要求所选地震记录加速度谱在该段的均值与设计反应谱相差不超过 10 ％ -20% ；二、对结构基本周期 T1 附近 段加速度反应谱均值进行控制（可近似对结构基本周期 T1 处加速度反应谱值进行控制） ，要求与设计反应谱相差不超过 10 ％ -20% 。 3.4 、双指标控制 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 经比较：用 0.5464 系数调整了峰值的 1940, El Centro Site, 270 Deg 实录波生成的长周期加速度反应谱符合 E2 设计加速度反应谱的双指标控制。 3.4 、双指标控制 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 3.5 、双指标控制 3 、 设计加速度时程的确定（选用实录波） 3.5 、持时 持续时间的概念不是指地震波数据中总的时间长度。持时 Td 的定义可分为两大类，一类是以地震动幅值的绝对值来定义的绝对持时，即指地震地面加速度值大于某值的时间总和，即绝对值的时间总和 ， k 常取为 0.05 ；另一类为以相对值定义的相对持时，即最先与最后一个 之间的时段长度， k 一般取 0.3 ～ 0.5 。不论实际的强震记录还是人工模拟波形，一般持续时间取结构基本周期的 5 ～ 10 倍。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 3.6 、与设计反应谱计算结果比较 《 公路桥梁抗震设计细则 》 ： 《 建筑抗震设计规范 GB50011_2001 条文说明 》 ： 对桥梁结构，也可采用基底剪力结果比较 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 3.6 、与设计反应谱基底剪力比较 设计反应谱基底剪力： 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 3.6 、与设计反应谱基底剪力比较 某墩柱时程基底剪力： 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 3.7 、最终确定所选波是否符合条件 根据以上各方面的控制比较，说明程序提供的 1940, El Centro Site, 270 Deg 实录波经用 0.5464 系数调整了峰值后适合作为本桥 E2 地震作用下的设计加速度时程。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 3.8 、用户导入其它地震波或自定义地震波 fn.thd. * UNIT,M,kN *TYPE,ACCEL *DATA 0.0000, -0.0047 0.0200, -0.0057 0.0400, -0.0070 0.0600, -0.0084 0.0800, -0.0061 0.1000, -0.0063 0.1200, -0.0090 *SGSw *TITLE, Earthquake Record *TITLE, *X-AXIS, Time (sec) *Y-AXIS, Ground Accel. (g) *UNIT&TYPE, GRAV, ACCEL *FLAGS, 0, 0 *DATA 0.0000, -0.0047 0.0200, -0.0057 0.0400, -0.0070 0.0600, -0.0084 0.0800, -0.0061 0.1000, -0.0063 0.1200, -0.0090 *ENDDATA 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 3.9 、按以上原则继续选波 最终选择出符合条件的多条实录地震波 桥 梁 抗 震 培 训 JTG/T B02-01-2008 3 、 设计加速度时程的确定（选用实录波） 4 、时程分析中恒载效应的考虑 4.1 、时程分析中考虑恒载效应的必须性 根据在桥梁动力分析时，一般取成桥阶段分析，此时自重恒载已经对结构变形，内力产生了影响。在动力分析时，必须考虑自重恒载的初始效应。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4 、时程分析中恒载效应的考虑 4.2 、 Civil 时程分析中考虑恒载效应 在程序中，做时程分析时通过“时程荷载工况－加载顺序”对话框考虑恒载效应，当前时程荷载工况可在前次荷载工况（可以是时程荷载、静力荷载、最后一个施工阶段荷载、初始内力状态）作用下的位移、速度、加速度、内力状态下继续分析。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4.2 、 Civil 时程分析中考虑恒载效应 考虑恒载效应 非线性振型叠加法：接续非线性振型叠加法 静力法 非线性直接积分法 对于线性时程分析，其时程结果和静力结果是可以进行叠加的，本例主要讨论非线性时程分析情况。在 Civil 时程分析中，做接续分析时，只能接续相同类型的分析工况 4 、时程分析中恒载效应的考虑 非线性直接积分法 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4.2 、 Civil 时程分析中考虑恒载效应 非线性振型叠加法： （ 1 ）定义一个斜坡类型的无量纲加速度时程函数“ RAMP ”如图，在相对结构第一周期较长（如 10 倍）的时间段上，从 0 到 1 线性增加，且在相等的时间段上保持恒定。 （ 2 ）定义一个非线性振型叠加法分析工况如下图，分析时间为“ RAMP ”函数持续时间，振型阻尼输入高阻尼比： 0.999 ，其它默认。 （ 3 ）接续动力非线性振型叠加法分析工况。 4 、时程分析中恒载效应的考虑 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4.2 、 Civil 时程分析中考虑恒载效应 4 、时程分析中恒载效应的考虑 1 、避开结构基本周期的长时间加载 2 、高阻尼使结构后续振动迅速衰减 3 、无量纲加速度 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4.2 、 Civil 时程分析中考虑恒载效应 4 、时程分析中恒载效应的考虑 直接积分法： （ a ）与振型叠加法一样定义函数，接续直接积分法分析； （ b ）使用静力法。 （ 1 ）定义一个斜坡类型的无量纲函数。 （ 2 ）定义非线性静力法分析工况，分析时间为 1S ，其它默认。 （ 3 ）接续动力非线性直接积分法分析工况。 （静力法具体内容参见用户手册） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4.2 、 Civil 时程分析中考虑恒载效应 4 、时程分析中恒载效应的考虑 1 、函数为无量纲 2 、静力荷载工况都定义 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4.2 、 Civil 时程分析中考虑恒载效应 4 、时程分析中恒载效应的考虑 综述： （ a ）使用重力加速度 g 作为时程函数时，只能考虑能转换为质量的荷载效应，包括：模型自重、能转换为质量的荷载、节点质量。对于预应力荷载是不能考虑的； （ b ）使用静力法。可以考虑所有静力荷载工况，所以在使用直接积分法时，优先选择静力法来考虑恒载效应。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4.3 、空间模型建立及荷载施加 空间动力分析模型的建立，延性构件抗弯刚度反应谱分析中需做相应折减，时程分析中需对可能进入塑性的构件运用弹塑性梁单元（分布铰或纤维模型）或用弯曲弹簧模型（集中铰）。 自振特性分析 振型组合方法的确定 地震作用分量组合的确定 桥 梁 抗 震 培 训 JTG/T B02-01-2008 4 、时程分析中恒载效应的考虑 5 、截面属性求解 按现行的公路桥涵设计规范相应的规范验算桥墩的抗弯强度，但与 E1 的强度验算不完全相同 , 延性构件的有效截面抗弯刚度需折减 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5 、截面属性求解 求延性构件的有效截面抗弯刚度 利用规范公式 6.1.6 计算 理论方法求解 CIVIL 程序计算 通过轴压比、纵筋配筋率得 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.1 、理论方法求解 、 5 、截面属性求解 1 、确定 曲线 纤维模型（条带法、将材料的应力－应变关系曲线转换成截面内力－变形关系曲线） 基本假定： （ 1 ）平截面假定； （ 2 ）剪切应变的影响忽略不计； （ 3 ）钢筋与混凝土之间无滑移现象 一般采用逐级加变形的方法求 曲线。 2 、根据 曲线确定屈服弯矩 、屈服曲率 一般采用几何作图法（包括等能量法、通用屈服弯矩法等）将确定的 曲线近似简化为双折线型或三折线型恢复力模型，规范 7.4.4 推荐的是几何作图法中的等能量法将曲线 转换为双折线理想弹塑性恢复力模型。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2 、 Civil 程序计算 、 5 、截面属性求解 对截面进行配筋设计后，将程序中美国联邦紧急管理厅出版的 《 房屋抗震加固指南 》 FEMA 定义的基本铰属性，分配给定义好的单元，自动计算屈服面特性值，得到截面屈服弯矩 。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 1 、用动力弹塑性模块中的纤维模型来求解屈服弯矩 、 。 2 、用动力弹塑性模块中的骨架模型来求解屈服弯矩 、 。 3 、用静力弹塑性模块中的铰属性来得到屈服弯矩 、 。 5.2.1 、 Civil 程序（纤维模型 ) 计算 、 1 、纤维截面的划分原则。 （ 1 ）根据横向和纵向钢筋布置，将截面初步分为钢筋区域和混凝土区域，混凝土又分为受约束和不受约束两类。 （ 2 ）根据截面受力特点，对非线性变化很剧烈的部分要有一定的细化，但是具体的细化程度要有效把握，不可过大或过小。 （ 3 ）可在纤维单元中添加用以模拟钢筋与混凝土之间粘结滑移效应的拉拔纤维以及模拟裂缝面的“裂面效应”的隙缝纤维以弥补普通纤维模型对充分粘结假定的局限性。 采用先粗后细原则 —— 第一步粗划分 ： 考虑箍筋对混凝土的约束作用，一般可将保护层范围内的混凝土划分为非约束混凝土区域，剩下的就是约束混凝土区域； 第二步细划分： 对某些区域进行细化。荷载后期，伴随着钢筋滑移、混凝土开裂和大的塑性变形以及外围混凝土的脱落，非约束混凝土在后期所起的作用是不大的，边缘纤维有向中间纤维逐步卸载的趋势。于是，对非约束混凝土可以选用较大的纤维面积，而对约束混凝土区域的外缘要细化，再逐步过渡到中部适当放大。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、 Civil 程序（纤维模型）计算 、 1 、纤维截面的划分原则。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、 Civil 程序（纤维模型）计算 、 2 、纤维的本构模型。 约束与非约束混凝土纤维一般使用程序提供的修正的 Kent & Park 模型。一定要正确理解该本构模型，参数输入要准确，否则将导致最终结果完全错误。为了方便用户输入，专门提供 Kent & Park 模型本构计算器。 Kent & Park 模型本构计算器 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、 Civil 程序（纤维模型）计算 、 2 、纤维的本构模型。 钢筋纤维可使用近似的理想弹塑性骨架曲线、考虑了 Bauschinger ”效应和硬化阶段的“ Menegotto-Pinto ”模型或考虑了流动阶段和硬化阶段的三折线骨架曲线。理想弹塑性模型适用于结构破坏时钢筋应变未进入强化段， “ Menegotto-Pinto ”模型的优点在于可考虑钢筋的“ Bauschinger ”效应，而三折线骨架曲线则可较准确地描述钢筋的大变形性能。本桥计算采用 Menegotto-Pinto ”模型。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、 Civil 程序（纤维模型）计算 、 3 、截面的纤维划分。 对于墩柱不同的箍筋配筋处应进行不同的纤维截面分割，本桥墩顶及墩底 2 米处箍筋间距为 10cm ，墩身中部箍筋间距为 20cm ，所以建立 2 个纤维截面。截面纤维划分参考前述纤维划分原则。 截面的纤维划分 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、 Civil 程序（纤维模型）计算 、 4 、施加单调递增弯矩及定轴力。 节点动力荷载施加单调递增弯矩 时变静力荷载施加定轴力 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、纤维模型计算 曲线 5 、“时程分析结果”－“纤维截面分析结果”查看墩根部绕 Y 轴 曲线 曲线 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、纤维模型计算顺桥向 、 6 、根据保护层混凝土初始开裂时对应弯矩查看墩根部顺桥向开裂弯矩 桥 梁 抗 震 培 训 JTG/T B02-01-2008 墩根部单元开裂弯矩 1176 kNm ，屈服曲率为 0.0004174rad/m 。 截面开裂状态图 5.2.1 、纤维模型计算顺桥向 、 7 、根据最外层受拉钢筋屈服时对应弯矩查看墩根部顺桥向截面屈服弯矩 截面屈服状态图 墩根部单元屈服弯矩 3274kNm ，屈服曲率为 0.003162rad/m 。 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、纤维模型计算 8 、根据受拉纵筋应变达到极限拉应变找到顺桥向截面极限曲率 截面极限曲率状态图 墩根部单元极限曲率为 0.01595rad/m 。对应弯 矩为 3470kNm 桥 梁 抗 震 培 训 JTG/T B02-01-2008 5.2.1 、由“等能量法计算 、 9 、根据 曲线利用“等能量法”求等效屈服弯矩，等效屈服曲率。 等效屈服弯矩 、等效屈服曲率 桥 梁 抗 震 培 训 JTG/T B02-01-2008 6 、顺桥向激励（纤维梁单元）动力模型 桥 梁 抗 震 培 训 JTG/T B02-01-2008 6.1 、全桥纤维弹塑性梁单元模型 桥 梁 抗 震 培 训 JTG/T B02-01-2008 顺桥向地震激励时，因墩柱反弯点出现在墩顶处，塑性铰由墩底截面向上发展， 所以墩底处构件应细化，为了在后面方便建立等效 Giberson 弯曲弹簧模型，也 为了方便提取纤维弹塑性梁单元节点转角结果，每个纤维单元积分点选 1 ，但 此时要注意单元一定要细分。 墩底局部 NTH 法（纤维弹塑性梁单元） 6.2 、顺桥向地震作用下墩底弯矩曲率曲线 NTH 法（纤维弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 在顺桥向地震激励下，墩底截面的最大弯矩可达 3735kNm ，大于在恒载作用下的 截面等效屈服弯矩 3689kNm ，小于截面极限弯矩 3799kNm 。满足大震不倒但不满 足大震可修。在时程中首次屈服弯矩为 3297kNm ，与单调屈服弯矩 3273kNm 基本 相当。 墩底弯矩曲率曲线 某时刻墩底截面首次屈服 6.3 、顺桥向地震作用下墩底塑性铰发展位置 桥 梁 抗 震 培 训 JTG/T B02-01-2008 查看在顺桥向地震激励下，墩底纤维梁单元弯矩最大值判断塑性铰在时程中 的发展位置。下图为最后屈服的截面滞回曲线。可知墩底由下至上四个单元进 入屈服状态。由图可看出，屈服后截面滞回曲线明显比屈服前开裂后饱满，开 裂后屈服前也基本呈非线性弹性。 塑性铰等效长度为： NTH 法（纤维弹塑性梁单元） 6.4 、顺桥向地震作用下墩顶位移曲线 NTH 法（纤维弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 在顺桥向地震激励下，墩顶在 5.61s 处达到最大位移 9.114cm 。 6.5 、顺桥向地震作用下桥墩塑性铰转角 NTH 法（纤维弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 由“结果” —— “分析结果表格” —— “非弹性铰” —— “变形” 查看该墩底四个进入塑性的纤维梁单元在时程中在 5.61 秒处达到的曲率。 根据共轭梁法可求得整个桥墩构件的塑性转角为： 此即为 《08 抗震细则 》 中的 7 、顺桥向激励（ Giberson ）动力模型 桥 梁 抗 震 培 训 JTG/T B02-01-2008 7.1 、 Giberson 集中铰弹塑性梁单元原理 桥 梁 抗 震 培 训 JTG/T B02-01-2008 计算原理： 把整个单元作为弹性材料，在外力作用下曲率逞直线分布，单元只发生弹性变形；单元的塑性变形全部集中于构件的两端，用 2 个零长度、配置在单元节点处的弯曲塑性弹簧来表示。 集中铰定义对话框 NTH 法（ Giberson 集中铰弹塑性梁单元） 7.2 、 Giberson 集中铰弹塑性梁单元滞回模型 桥 梁 抗 震 培 训 JTG/T B02-01-2008 钢筋混凝土构件滞回模型一般选择经典的 Clough 双折线、 Takeda 三折线。 本桥选择 Takeda 三折线滞回模型。 滞回模型定义 NTH 法（ Giberson 集中铰弹塑性梁单元） 7.3 、 Giberson 集中铰弹塑性梁单元骨架曲线 桥 梁 抗 震 培 训 JTG/T B02-01-2008 钢筋混凝土构件骨架曲线一般为 2 折线或 3 折线，本桥选择 Takeda 三折线滞回模型，相应选择开裂强度、屈服强度为双折线定义强度，相应的刚度折减率可按如下求解： 当墩底单元细分后，可近似认为单元节点间无外荷载且单元两节点处弯矩正对称，此时端截面处弯矩 — 曲率曲线与端截面处弯矩 — 转角曲线成比例。所以根据纤维截面分析结果自定义骨架曲线关键点： 骨架曲线定义 NTH 法（ Giberson 集中铰弹塑性梁单元） 7.4 、顺桥向位移曲线 桥 梁 抗 震 培 训 JTG/T B02-01-2008 NTH 法（ Giberson 集中铰弹塑性梁单元） 在顺桥向地震激励下，墩顶在 5.64s 处达到最大位移 9.463cm 。 7.5 、顺桥向地震作用下桥墩塑性铰转角 NTH 法（ Giberson 集中铰弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 由“结果” —— “分析结果表格” —— “非弹性铰” —— “变形”查看该墩底四个进入塑性的纤维梁单元在时程中的最大转角（在 5.63 秒处达到）。 可求得整个桥墩构件的塑性转角为： 此即为 《08 抗震细则 》 中的 7.6 、顺桥向地震作用下两结果比较 NTH 法（ Giberson 集中铰弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 最 不利时刻 墩 顶最大 位移 （ cm ） 墩柱 最大 转角 （ rad ） 纤维 模型 5.61s 9.114 0.001845 集中 铰模型 5.63s 9.463 0.00197 8 、横桥向激励（纤维梁单元）动力模型 桥 梁 抗 震 培 训 JTG/T B02-01-2008 8.1 、全桥纤维弹塑性梁单元模型 桥 梁 抗 震 培 训 JTG/T B02-01-2008 与顺桥向分析模型不一致，墩顶墩底均需要布置塑性铰。 墩底局部 NTH 法（纤维弹塑性梁单元） 整体模型 8.2 、横桥向地震作用下墩底弯矩曲率曲线 NTH 法（纤维弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 在横桥向地震激励下，墩底截面受到剧烈变化的轴力影响，时程中首次屈服时对应弯矩为 3801kNm ，远大于在恒载下的屈服弯矩 2691kNm 。与定轴力弯矩曲率曲线比较发现变轴力使得结构刚度退化明显。 横桥向变轴力墩底弯矩曲率曲线 顺桥向定轴力墩底弯矩曲率曲线 8.3 、横桥向地震作用下墩顶轴力时程图 NTH 法（纤维弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 在横桥向地震激励下，墩柱所承受的轴力与恒载时相比急剧变化，最大达到 8947kN ，最小达到 3012kN 。墩柱轴压比由初始的 0.31 变为 0.16—0.48 。 8.4 、顺桥向地震作用下墩顶轴力时程图 NTH 法（纤维弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 而在顺桥向地震激励下，墩柱所承受的轴力与恒载时相比基本无变化，最大为 5799kN ，最小为 5703kN 。 8.5 、横桥向地震作用下墩顶横桥向位移时程图 NTH 法（纤维弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 在横桥向地震激励下，墩顶在 2.75s 达到横桥向最大位移为 5.935cm 。 8.6 、结论 NTH 法（纤维弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 在 顺桥向地震激励 下，墩柱所承受的轴力与恒载时相比基本无变化，此时用承受恒载压力的墩柱 M—Phi 曲线来进行截面屈服判别是没任何问题的，此时基于此曲线的用户自定义 Giberson 集中铰模型也是成立的。 但在 横桥向地震激励 下，墩柱承受的轴压力急剧变化，此时再用承受恒载压力的墩柱 M—Phi 曲线来进行截面屈服判别是有问题的，用户自定义 Giberson 集中铰模型也必须考虑 P—M—M 相关面，此时可选择程序中的 ACI 或 ACJ 来自动计算。 建议 在横桥向地震激励下，最好使用能考虑轴力变化的纤维模型。 8.6 、结论 NTH 法（ Giberson 集中铰弹塑性梁单元） 桥 梁 抗 震 培 训 JTG/T B02-01-2008 墩顶 顺桥向 最大位移 （ cm ） 墩顶横桥向最大位移 （ cm ） 弹塑性时程（纤维模型） 9.114 5.935 弹性时程 7.42 6.23 在弹塑性时程顺桥向分析中 ，因墩底出现塑性铰而墩顶没出现塑性铰，此时墩底塑性铰的转动导致墩顶顺桥向位移比弹性时程时偏大； 而当 在弹塑性时程横桥向分析中 ，因墩底墩顶都出现塑性铰，此时的横向位移并不一定比弹性时程的位移大。 规范 7.4.2 条是对截面层次上的曲率延性系数验算的变化形式 规范 7.4.6 条是对结构层次上的位移延性系数验算的变化形式 桥 梁 抗 震 培 训 JTG/T B02-01-2008 变形验算 抗震结构（弹塑性梁单元）的变形验算 桥 梁 抗 震 培 训 JTG/T B02-01-2008 弹塑性梁单元（ 抗震结构 ）的变形验算为： （ 1 ）结构层次的最大地震位移验算，主要为墩顶位移验算；安装了隔震层的 隔震结构 的变形主要为隔震层的变形验算。 （ 2 ）截面层次的梁单元的曲率验算。 变形验算 （ 3 ）结构层次的塑性铰转角验算。 规范 7.4.2 条 规范 7.4.3 条 抗震结构（弹塑性梁单元）的变形验算 桥 梁 抗 震 培 训 JTG/T B02-01-2008 变形验算 结构层次的塑性铰容许转角： 规范 7.4.3 条 对于本桥 结构层次的顺桥向墩顶最大位移： 规范 7.4.7 条 对于本桥 抗震结构（弹塑性梁单元）的变形验算 桥 梁 抗 震 培 训 JTG/T B02-01-2008 变形验算 结构层次的横桥向墩顶最大位移： 需用到静力弹塑性模块中 PUSHOVER 功能（非线性静力分析）。 抗震结构（弹塑性梁单元）的变形验算 桥 梁 抗 震 培 训 JTG/T B02-01-2008 变形验算 建立双墩模型并施加水平推力及上部压力： 抗震结构（弹塑性梁单元）的变形验算 桥 梁 抗 震 培 训 JTG/T B02-01-2008 变形验算 定义 PUSHOVER 工况： （ 1 ）一定要施加初始轴力（考虑 P-M-M) （ 2 ）高墩可考虑 P-Dalta 效应 （ 3 ）一般可采取位移控制 （ 4 ）荷载模式选择推力 抗震结构（弹塑性梁单元）的变形验算 桥 梁 抗 震 培 训 JTG/T B02-01-2008 变形验算 定义塑性铰： （ 1 ）可选择弯矩－旋转角；弯矩－曲率弯矩－曲率（分布） （ 2 ）可选择各内力互不相关和 P-M-M （ 3 ）骨架曲线可选择双折线、三折线（含日本 AIJ 管野公式）、 FEMA （ 4 ）屈服面可选择自动计算或用户输入 抗震结构（弹塑性梁单元）的变形验算 桥 梁 抗 震 培 训 JTG/T B02-01-2008 变形验算 大致判断四个铰区中先到达极限转角位置，将该区域内各个塑性铰塑性转角相加： 抗震结构（弹塑性梁单元）的变形验算 桥 梁 抗 震 培 训 JTG/T B02-01-2008 变形验算 由步骤数 621 步通过荷载－位移曲线 查看此时对应的位移：