2019-2020学年山东省枣庄市高一上学期期末考试数学试题 8页

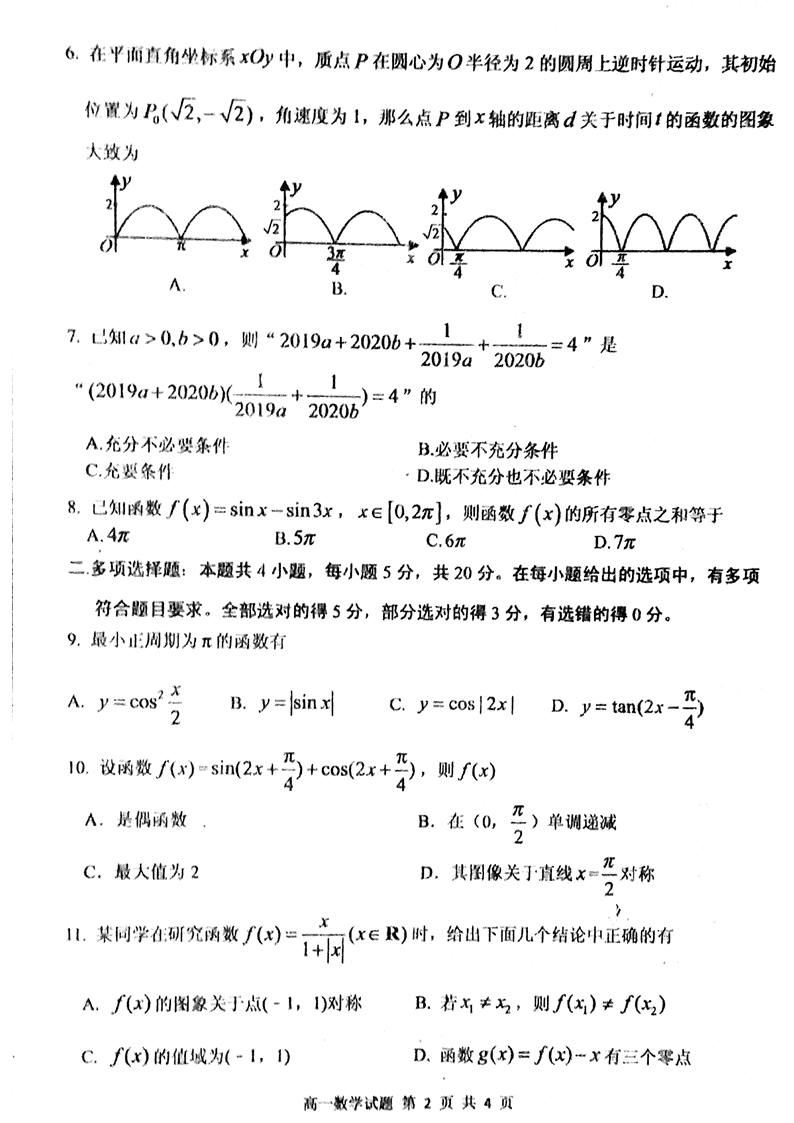
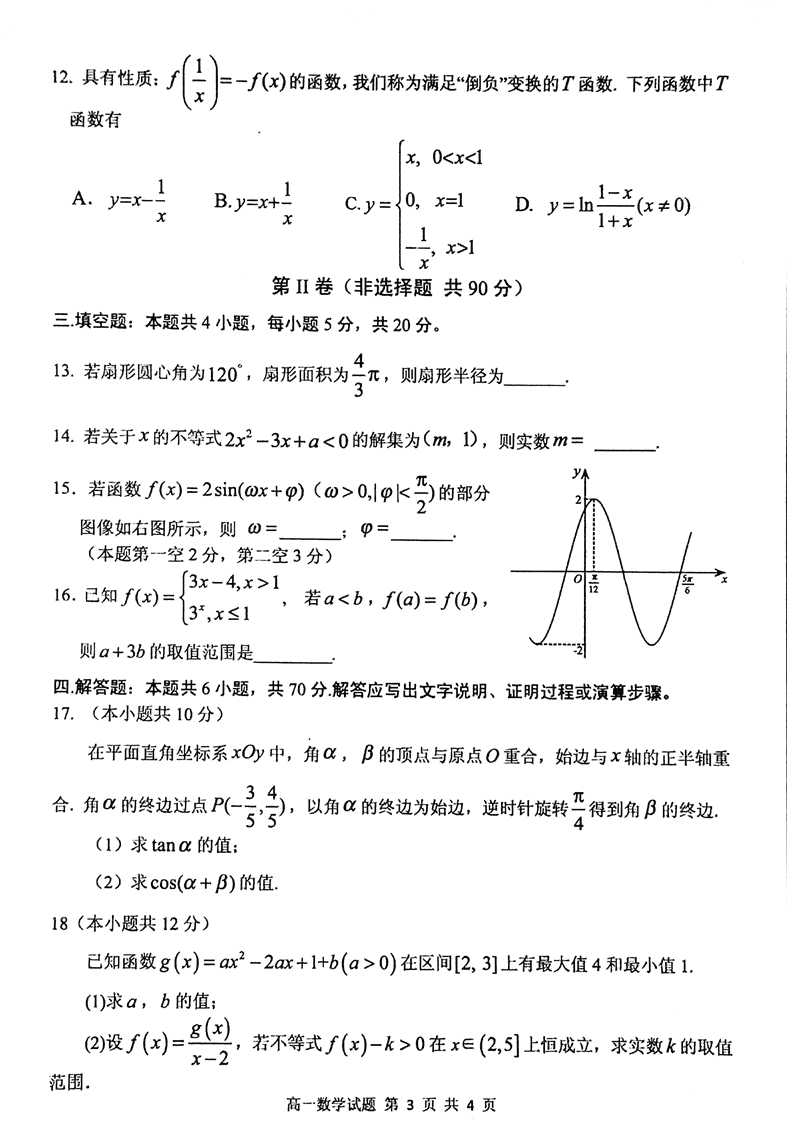
高一数学答案 第 1 页 共 4 页 高一数学试题参考答案及评分标准 2019.01 一、选择题 1 2 3 4 5 6 7 8 9 10 11 12 D B D C B C A D BC ABD BC AC 二、填空题 13. 2 14. 1 2 15. 2 ； 3 π （本题第一空 2 分，第二空 3 分） 16. ( ],8-¥ 三、解答题 17. 解：（ 1 ）由角α 的终边过点 34(,)55P - ， 得 34cos,sin55αα=-=.…………………………………………………………2 分 所以 sin4tan cos3 αα α==- .…………………………………………………………4 分 (或显然点 34(,)55P - 在单位圆上，所以 4 45tan 3 3 5 α ==- - .) （2）由（1）得 24sin22sincos,25ααα==- 227cos2cossin.25ααα=-=- …………………………………………………7 分 由题意 4 πβα=+， 所以cos()cos(2)4 παβα+=+cos2cossin2sin44 ππαα=- 22724172(cos2sin2)()22252550αα=-=-+= .…………………………10 分 18.解：（ 1 ） ( )gx∵ 开口方向向上，抛物线 ( )ygx= 的对称轴为直线 1x = ， ( )gx 在[ ]2,3 上单调递增. …………………………………………………2 分 ( ) ( ) () () min max 24411 39614 gxgaab gxgaab ì==-++=ïí ==-++=ïî 高一数学答案 第 2 页 共 4 页 解得 10ab==且 . …………………………………………………………6 分 （2） ( ) 0fxk->∵ 在 ( ]2,5xÎ 上恒成立， ( )minkfx<只需 () ( ) 2 gxfx x= - 2 211122222 xx xxxxx -+==+=-++---4³ .……………10 分 当且仅当 12 2x x-=- ，即 3x = 时等号成立. 4k<. …………………………………………………………………………12 分 19.解：（1） 13()sin2cos2122fxxx=++sin(2)13x π=++.……………3 分 由 222232kxkπππππ-£+£+，得 5 1212kxkππππ-££+. 所以， ()fx的单调递增区间是 5[,],1212kkkππππ-+ÎZ . ………6 分 （2） ()sin(2)13fxxπ=++， 由 [,]44x ππÎ- ，得 52[,]366x πππ+Î- ， …………………………………8 分 当 2 32x ππ+=，即 12x π= 时， ()fx有最大值 ()11212f π =+= ；………10 分 当 2 36x ππ+=- ，即 4x π=- 时， ()fx有最小值 11()1422f π-=-+= .…12 分 20 解：（ 1 ）由题意，当020x££ 时， ()100vx = ；……………………………2 分 当 20220x££ 时，设 ()vxaxb=+， 因为 (20)20100vab=+= ， (220)2200vab=+=， 所以 1 ,1102ab==. ……………………………………………………5 分 所以 100,020, () 1 110,202202 x vx xx ££ìï=í-+<£ïî . ………………………………………6 分 （2）依题意，并由（1）得 高一数学答案 第 3 页 共 4 页 2 100,020, () 1 110,202202 xx fx xxx ££ìï=í-+<£ïî . ………………………………………8 分 当 020x££ 时， ()fx的最大值为 (20)2000f = ； ……………………9 分 当 20200x<£ 时， 21()(110)60502fxx=--+； 当110x = 时， ()fx的最大值为 (110)6050f = .…………………………11 分 综上，当车流密度为 110 辆/千米时，车流量最大，最大值为 6050 辆/时.…12 分 21 解：（ 1 ）因 ( )fx的图象上相邻两个最高点的距离为π ，所以 ( )fx的最小正周期T π= ， 从而 2 2T πω ==. …………………………………………………………2 分 又因 ( )fx的图象关于直线 3 π=x 对称， 所以 2,0,1,2,,32kkππϕπ×+=+=±±L 因为 22 ππϕ-£< ，得 0k = ． 解得 2 236 πππϕ =-=- .………………………………………………………5 分 因此所求解析式为 () 3sin2 6fxxπæö=-ç÷èø.………………………………6 分 （2）由（1）得 33sin22264f ααπæöæö=×-=ç÷ç÷èøèø ，所以 1sin 64 παæö-=ç÷èø . 由 2 63 ππα<< 得0,62 ππα<-< 所以 2 2 115cos1sin1.6644 ππααæöæöæö-=--=-=ç÷ç÷ç÷èøèøèø …………………9 分 因此 3cossinsin266 πππαααéùæöæö+==-+ç÷ç÷êúèøèøëû sincoscossin6666 ππππααæöæö=-+-ç÷ç÷èøèø 高一数学答案 第 4 页 共 4 页 = 13151315 42428 +´+´= ．………………………………………………12 分 22 解：（1）定义域为 R 的函数 () x xfx ea ae= + 是偶函数，则 () ()fx fx-= 恒成立， 即 xx xx eaea aeae - - =++，故 1()()0xxaeea ---=恒成立. 因为 xxee-- 不可能恒为0 ，所以 1 0aa -=， 而 0a > ，所以 1a = ．…………………………………………………………2 分 （2）该函数 () 1x xfx e e= + 在 (0,)+¥ 上单调递增，证明如下 设任意 12,(0,)xxÎ+¥ ，且 12xx< ，则 1212 121212 1111()()()()()()xxxx xxxxfxfxeeeeeeee-=+-+=-+- 211212 12 1212 ()(1)() xxxxxx xx xxxx eeeeeeee eeee ---=-+= . ……………5 分 因为 120 xx<<，所以 12xxee< ，且 121,1xxee>>[] 所以 1212 12 ()(1) 0 xxxx xx eeee ee --< ，即 12()()0fxfx-<，即 12()()fxfx< . 故函数 () 1x xfx e e= + 在 (0,)+¥ 上单调递增．……………………………………8 分 （3）由（2）知函数 ()fx在 (0,)+¥ 上递增，而函数 ()fx是偶函数， 若存在实数 m ，使得对任意的 t Î R ，不等式 (2)(2)ftftm-<-恒成立． 则 22 tmt --< 恒成立，即 2222 tmt --< .……………………………10 分 即 223(44)40tmtm--+->对任意的t Î R 恒成立， 则 22(44)12(4)0mmD=---<， 得到 2(4)0m -<，故 mÎÆ，所以不存在．……………………………12 分