山东省泰安肥城市2020届高三数学适应性训练（一）试题（Word版附答案） 15页

2020 年高考适应性训练 数 学 试 题（一） 注意事项： 1．答题前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如 需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。 写在本试卷上无效。 3．考试结束后，将本试卷和答题卡一并交回。 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分. 在每小题给出的四个选项中，只 有一项是符合题目要求的． 1. 已知集合  2| 3 2 0A x x x    ,  = || 1| 1B x x   ,则 A B  A. | 0 2x x  B. | 0 1x x  C. | 2x x  D. |1 2x x  2. 已知  2 i i 2 iz   ,则 z = A. 3 B. 2 C. 1 D. 1 2 3. 下列结论正确的是 A. 残差点均匀分布的带状区域的宽度越窄，说明模型拟合精度越低. B. 在线性回归模型中,相关指数 =0.962R ,说明解释变量对于预报变量变化的贡献率约为 96%. C. 已知随机变量 2(2, )X N  ，若 (0 2) 0.4P X   ，则 ( 4) 0.2P X   . D. 设 ,a b 均为不等于 1 的正实数，则“ log 2 log 2b a ”的充要条件是“ 1a b  ”. 4. 若 3 n x x     的展开式中各项系数之和为 256 ，则展开式中 x 的系数是 A. 54 B. 81 C. 96 D. 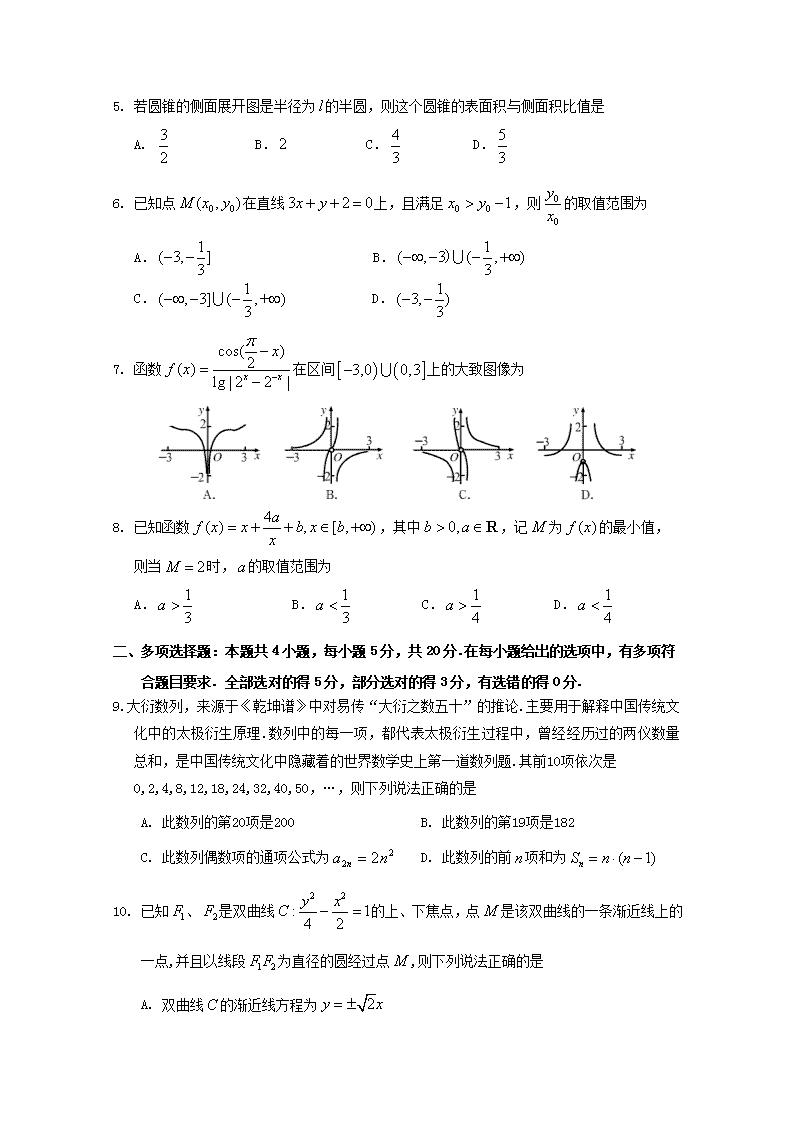106 5. 若圆锥的侧面展开图是半径为l 的半圆，则这个圆锥的表面积与侧面积比值是 A. 3 2 B． 2 C． 4 3 D． 5 3 6. 已知点 0 0( , )M x y 在直线3 2 0x y   上，且满足 0 0 1x y  ，则 0 0 y x 的取值范围为 A． 1( 3, ]3   B． 1( , 3 ( , )3    ） C． 1( , 3] ( ,+ )3     D． 1( 3, )3   7. 函数 cos( )2( ) lg | 2 2 |x x x f x      在区间   3,0 0,3  上的大致图像为 8. 已知函数 4( ) , [ , )af x x b x bx      ，其中 0,b a R ，记 M 为 ( )f x 的最小值， 则当 2M  时， a 的取值范围为 A． 1 3a  B． 1 3a  C． 1 4a  D． 1 4a  二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分.在每小题给出的选项中，有多项符 合题目要求. 全部选对的得 5 分，部分选对的得 3 分，有选错的得 0 分. 9. 大衍数列，来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统 文化中的太极衍生原理.数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数 量总和，是中国传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是 0,2,4,8,12,18,24,32,40,50，…，则下列说法正确的是 A. 此数列的第20项是200 B. 此数列的第19项是182 C. 此数列偶数项的通项公式为 2 2 2na n  D. 此数列的前 n 项和为 ( 1)nS n n   10. 已知 1F 、 2F 是双曲线 2 2 : 14 2 y xC   的上、下焦点，点 M 是该双曲线的一条渐近线上的 一点,并且以线段 1 2F F 为直径的圆经过点 M ,则下列说法正确的是 A. 双曲线C 的渐近线方程为 2y x  A B D Q C P B. 以 1 2F F 为直径的圆的方程为 2 2 2x y  C. 点 M 的横坐标为 2 D. 1 2MF F 的面积为 2 3 11. 已知定义在 R 上的函数 ( )f x 满足 ( )+ ( ) 0, ( 6) ( )f x f x f x f x     ，且对  1 2, 3,0x x   ，当 1 2x x 时，都有 1 1 2 2 1 2 2 1( ) ( ) ( ) ( )x f x x f x x f x x f x   ，则以下判 断正确的是 A. 函数 ( )f x 是偶函数 B. 函数 ( )f x 在 9 6 ， 单调递增 C. 3x  是函数 ( )f x 的对称轴 D. 函数 ( )f x 的最小正周期是12 12. 如图四棱锥 P ABCD ,平面 PAD  平面 ABCD ,侧面 PAD 是边长为 2 6 的正三 角形, 底面 ABCD 为矩形， 2 3CD  ，点Q 是 PD 的中点，则下列结论正确的是 A. CQ PAD 平面 B. PC 与平面 AQC 所成角的余弦值为 2 2 3 C. 三棱锥 B ACQ 的体积为 6 2 D. 四棱锥Q ABCD 外接球的内接正四 面体的表面积为 24 3 三、填空题：本题共 4 小题，每小题 5 分，共 20 分. 13. 用 0,1,2,3,4 这五个数字，可以组成 ▲ 个三位正整数. 14. 函数 2sin2cos)2sin()( 2 xxxxf   在 ],0[  上的最小值是 ▲ . 15. 已知一袋中装有红,蓝,黄,绿小球各一个，每次从中取出一个，记下颜色后放回. 当四 种颜色的小球全部取出时即停止，则恰好取 6 次停止的概率为 ▲ . 16. 已知圆 F ：  22 3 1x y   ，直线 : 2l y  ，则与直线l 相切且与圆 F 外切的圆的圆心 M 的轨迹方程为 ▲ .点 P 是圆心 M 轨迹上的动点,点 A 的坐标是  0,3 ， 则使 | | | | PF PA 取最小值时的点 P 的坐标为 ▲ . 四、解答题：本题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤. 17.（10 分） 已知数列 na 各项均为正数， 1 1a  ， 2 na 为等差数列，公差为 2. （1）求数列 na 的通项公式. （2）求 2 2 2 3 2 2 1 2 3=2 2 +2 2n n na aS a a   . 18. (12 分) 在 ABC 中，角 , ,A B C 的对边分别为 , ,a b c ,且 2 2 2(2 )( ) 2 cosb c b a c abc C    . （1）求角 A 的大小. （2）若 3B  ，D 为 ABC 外一点， 2, 1BD CD  ,四边形 ABDC 的面积是 5 3 24  ， 求 a . 19.（12 分） 条件①：图（1）中 4tan 2 3B   . 条件②：图（1）中 2 1 3 3AD AB AC    . 条件③：图（2）中三棱锥 A BCD 的体积最大. 从以上三个条件中任选一个，补充在问题（2）中的横线上，并加以解答. 如图（1）所示，在 ABC 中, 45ACB   ， 3BC  ，过点 A 作 AD BC ，垂足 D 在线段 BC 上，沿 AD 将 ABD 折起，使 90BDC   (如图（2）)，点 ,E M 分别 为棱 ,BC AC 的中点． （1）求证：CD ME . （2）已知_____________,试在棱 CD 上确定一点 N ，使得 EN BM ，并求锐二面角 M BN C  的余弦值． 注：如果选择多个条件分别解答，按第一个解答计分. 20.（12 分） 图（2） M A B C E D •B D A C 图（1） 已知椭圆   2 2 2 2: 1 0x yC a ba b     的离心率为 1 2 ，左、右焦点分别是 1F 、 2F ，不经过 左焦点 1F 的直线 2 0x y   上有且只有一个点 A 满足 1 2 90F AF   . （1）求椭圆C 的标准方程. （2）与圆 2 2 2x y  相切的直线l ：  y kx m 交椭圆C 于 P 、Q 两点，若椭圆上存在 点 M 满足   0     OM OP OQ ，求四边形OPMQ 面积的取值范围. 21.（12 分） 已知函数 ( ) ln 1f x x x ax   ( )aR . （1）讨论 ( )f x 的零点个数. （2）正项数列 na 满足 1 2 3a  ， 1 +1ln +12 n n aa   ( n N )， 求证： 1 2 1 1 1 1 n na a a     . 22.（12 分） 书籍是人类的智慧结晶和进步阶梯，阅读是一个国家的文化根基和创造源泉.2014 年以来，“全 民阅读”连续 6 年被写入政府工作报告.某学校为提高师生阅读书籍的热情，举行了“博雅杯” 科技知识大奖赛，比赛分两个阶段进行：第一阶段由评委给所有参赛选手评分，并确定优胜 者；第二阶段为附加赛，参赛选手由组委会按规则另行确定.数据统计员对第一阶段的分数进 行了统计分析，这些分数 x 都在  70,100 内，以 5 为组距画频率分布直方图时（设 Y频率“ ”组距 ），发现Y 满足： Y  8 109 16300 1 1615 20 n n k nn        ， ， , ,5 5( 1)n n x n   N . （1）试确定 n 的所有取值，并求 k . （2）组委会确定：在第一阶段比赛中低于85分的参赛选手无缘获奖也不能参加附加赛； 分数在 95,100 的参赛选手评为一等奖；分数在 90,95 的参赛选手评为二等奖，但通过附 加赛有 1 11 的概率提升为一等奖；分数在 85,90 的参赛选手评为三等奖，但通过附加赛有 1 7 的 概率提升为二等奖（所有参加附加赛的获奖选手均不降低获奖等级）.已知 A 和 B 均参加了本 次比赛，且 A 在第一阶段评为二等奖. （ⅰ）求 B 最终获奖等级不低于 A 的最终获奖等级的概率. （ⅱ）已知 A 和 B 都获奖，记 A 、 B 两位参赛选手最终获得一等奖的人数为 ，求 的 分布列和数学期望. 2020 年高考适应性训练 数学（一）参考答案及评分标准 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分. 题号 1 2 3 4 5 6 7 8 答案 D C B A A B C D 二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分. 全部选对的得 5 分，部分选对的 得 3 分，有选错的得 0 分. 题号 9 10 11 12 答案 AC ACD BCD BD 三、填空题：本题共 4 小题，每小题 5 分，共 20 分. 13. 100 14. 2 1 2  15. 75 512 16. 2 12x y   6, 3  四、解答题：本题共 6 小题，共 70 分. 17.（10 分） 解：（1） 1 1a  ， 2 1 1a  ， 2 na 为等差数列，公差为 2,  2 2 1= ( 1) 2=2 1na a n n    , ……………………………2 分  0na  ，通项公式 2 1na n  . ………………………………4 分 （2） 2 2 2 3 2 2 1 2 3=2 2 +2 +2n n na aS a a  , 2 3=1 2 3 2 5 2 2 1 2n nS n         （ ） 2 3 4 +12 1 2 3 2 5 2 (2 1) 2n nS n          ………………………………6 分 以上两式相减，得 2 3 +11 2 2 2 2 2 2 2 (2 1) 2n n nS n             ………………………………8分 2 3 +12 2 2 (2 1) 2n nn      +16 (2 3) 2nn     ……………………………9 分 ∴ +16+(2 3) 2n nS n   . ………………………………10 分 18.（12 分） 解：（1）∵角 , ,A B C 的对边分别为 , ,a b c ，且  2 2 22 2 cosb c b a c abc C    , ∴   2 2 22 cos2 b c b c a a Cbc     , ……………………………2 分 由余弦定理得： 2 )cos cosb c A a C （ , ……………………………3 分 由正弦定理得： 2sin cos sin cos sin cosB A C A A C  ，又 A B C    , ∴  2sin cos sin cos cos sin sin sinB A C A C A C A B     , ……………………5 分 ∵sin 0B  ，∴ 1cos 2A  ∵  0,A  ,∴ 3A  . ……………………………6 分 （2）在 BCD 中， 2, 1BD CD  ,由余弦定理得： 2 2 21 2 2 1 2cos 5 4cosBC D D       ,又 3A B   , ∴ 3C  ∴ ABC 为等边三角形， ………………………………8 分 ∴ 21 sin2 3ABCS BC     = 5 3 3 cos4 D ，又 1= sin sin2BDCS BD DC D D    ， ∴ 5 3 5 3sin 3 cos 2sin4 4 3ABDCS D D D         四边形 = 5 3 24  , …………10 分 sin( ) 13D    ， (0, )D  5 6D   , ……………………………11 分 2 55 4cos 5 4cos 5+2 36BC D       , 5 2 3BC   ， 即 5 2 3a   . ………………………………12 分 19.（12 分） 解：（1） , ,CD AD CD BD AD BD D   , CD ABD  平面 ,  AB ABD 平面 , CD AB  . ………………………………………………2 分 又 ,M E 分别为 ,AC BC 的中点， // ,ME AB .CD ME  …………………………………3 分 （2）方案一：选① 在图(1)所示的 ABC 中，由 2 4 2tantan 2 3 1 tan BB B     , 解得 tan 2B  或 1tan 2B   (舍去). 设 AD CD x  ，在 Rt ABD 中， tan 23 AD xB BD x    , 解得 2x  ， 1BD  . …………………………………5 分 以点 D 为原点，建立如图所示的空间直角坐标系 D xyz , 1(0,0,0), (1,0,0), (0,2,0), (0,0,2), (0,1,1), ( ,1,0)2D B C A M E ，则 ( 1,1,1)BM   . 设 (0, ,0)N a ,则 1( , 1,0)2EN a   . , 0EN BM EN BM      , 即 1 , 1,0) ( 1,1,1) 02 a    （ ， 1 2a  ， 1(0, ,0)2N , 当 1 2DN  (即 N 是CD 的靠近 D 的一个四等分点）时， EN BM . ………8 分 取平面 BNM 的一个法向量 ( , , )x y zn ,且 1( 1, ,0)2BN   , 由 0 0 BN BM        n n ,得 2 0 0 x y x y z        ，令 1x  ，则 (1,2, 1) n . 取平面 BNC 的一个法向量 (0,0,1)m , …………………………………10 分 2 2 2 (0,0,1) (1,2, 1) 6cos | || 61 2 ( 1)           , | m nm n m n , …………………………………11 分 锐二面角 M BN C  的余弦值为 6 6 . …………………………………12 分 方案二：选② 在图(1)所示的 ABC 中， , ( ) (1 )BD BC AD AB BD AB BC AB AC AB AB AC                          , A B E C M x y z ND A B E C M x y z ND A B E C M x y z ND 又因为 2 1 3 3AD AB AC    ,由平面向量基本定理知 1 3   ，即 1BD  . ……………5 分 以点 D 为原点，建立如图所示的空间直角坐标系 D xyz , 1(0,0,0), (1,0,0), (0,2,0), (0,0,2), (0,1,1), ( ,1,0)2D B C A M E ，则 ( 1,1,1)BM   . 设 (0, ,0)N a ,则 1( , 1,0)2EN a   . , 0EN BM EN BM      . 即 1 , 1,0) ( 1,1,1) 02 a    （ ， 1 2a  ， 1(0, ,0)2N , 当 1 2DN  (即 N 是CD 的靠近 D 的一个四等分点)时, EN BM . …………8 分 取平面 BNM 的一个法向量 ( , , )x y zn ,且 1( 1, ,0)2BN   , 由 0 0 BN BM        n n ,得 2 0 0 x y x y z        ，令 1x  ，则 (1,2, 1) n . 取平面 BNC 的一个法向量 (0,0,1)m , …………………………………10 分 2 2 2 (0,0,1) (1,2, 1) 6cos | || 61 2 ( 1)           , | m nm n m n , …………………………………11 分 锐二面角 M BN C  的余弦值为 6 6 . …………………………………12 分 方案三：选③ 在图(1)所示的 ABC 中，设 (0 3)BD x x   ，则 3CD x  , ∵ , 45AD BC ACB    ，∴ ADC 为等腰直角三角形，∴ 3AD CD x   , 折起后 ,AD DC AD BD  ,且 BD DC D ， ∴ AD BCD 平面 .又 90BDC   ，  1 (3 )2BCDS x x   , 3 21 1 1 1(3 ) (3 ) ( 6 9 )3 3 2 6A BCD BCDV AD S x x x x x x          , (0,3)x , A B E C M x y z ND 令 3 21( ) ( 6 9 )6f x x x x   ， 1) ( 1)( 3)2f x x x    , 当 0 1x  时， ( ) 0f x  ，当1 3x  时， ( ) 0f x  , ∴ 1x BD  时，三棱锥 A BCD 体积最大. …………………………………5 分 以点 D 为原点，建立如图所示的空间直角坐标系 D xyz , 1(0,0,0), (1,0,0), (0,2,0), (0,0,2), (0,1,1), ( ,1,0)2D B C A M E ,则 ( 1,1,1)BM   . 设 (0, ,0)N a ,则 1( , 1,0)2EN a   . , 0EN BM EN BM      , 即 1 , 1,0) ( 1,1,1) 02 a    （ ， 1 2a  ， 1(0, ,0)2N , 当 1 2DN  (即 N 是CD 的靠近 D 的一个四等分点)时, EN BM . ………8 分 取平面 BNM 的一个法向量 ( , , )x y zn ,且 1( 1, ,0)2BN   , 由 0 0 BN BM        n n ,得 2 0 0 x y x y z        ，令 1x  ，则 (1,2, 1) n . 取平面 BNC 的一个法向量 (0,0,1)m , …………………………………10 分 2 2 2 (0,0,1) (1,2, 1) 6cos | || 61 2 ( 1)           , | m nm n m n , …………………………………11 分 锐二面角 M BN C  的余弦值为 6 6 . …………………………………12 分 20.（12 分） 解：（1）直线 2 0  x y 上有且只有一个点 A 满足 1 2 90F AF   , 直线 2 0  x y 与圆 2 2 2 x y c 相切，  22 0 0 2 1 + 1 c     ,  1c . ………………………………………1 分 又 1 2 c a ,  2a ， 2 2 2 3  b a c , A B E C M x y z ND 椭圆 C 的方程为 2 2 14 3  x y . ………………………………………3 分 （2） 直线l ：  y kx m 与圆 2 2 2x y  相切， 2 2 1 m k    ， 即  2 22 1m k  ，且 2 2m  . ………………………………………4 分 设  1 1,P x y ，  2 2,Q x y ，  0 0,M x y 由 2 2 14 3     y kx m x y 消去 y 得, 2 2 24 3 8 4 12 0    k x kmx m ,  1 2 2 8 4 3    kmx x k ， 2 1 2 2 4 12 4 3   mx x k ,   1 2 1 2 2 62 4 3       my y k x x m k . …………………………………5 分       OM OP OQ ， 0 2 0 2 8 4 3 6 4 3         kmx k my k ，又 M 在椭圆C 上,  2 2 2 2 8 6 4 3 4 3 14 3              km m k k ， 24 3 2   k m . ………………………………7 分 设 PQ 的中点为 E ，则   2       OM OP OQ OE ,  0,0O 到 :l y kx m  的距离为 = 2d , ∴四边形 OPMQ 的面积 12 2 22POQS S PQ d PQ       …………8 分      2 2 2 2 2 22 64 4 4 12 4 3 2 1 4 3 k m m k k k             2 2 2 22 4 2 2 3 2 3 4 3 4 3 k k k k        2 2 2 12 3 4 3 k k   ,……………………………10 分 令   2 2 2 2 1 1 1 4 3 2 8 6 kf k k k     ， 28 6 6k   ，  1 1 3 2f k  ,  2 6S  ， 四边形OMPN 面积的取值范围为 2, 6 . …………………………………12 分 21.（12 分） 解：（1） ( )f x 的定义域为 | 0x x  ，令 ( ) ln 1 0f x x a     ,则 1eax  . 当 10 e ( ) 0ax f x   时， ；当 1eax  时, ( ) 0f x  ，  ( )f x 在 1(0,e )a 单调递减，在 1(e , )a  单调递增，  ( )f x 的最小值为 1 1(e ) 1 ea af    . …………………………………2 分 当 1a  时， 11 e 0a  ，此时 ( )f x 无零点. 当 1a  时， 11 e 0a  ，此时 ( )f x 只有一个零点. …………………………………3 分 当 1a  时， 11 e 0a  ， (e ) 1 0af   ，又 1e ea a ,  ( )f x 在 1(e , )a  上有且只有一个零点. …………………………………4 分 (e ) 1 2 ea af a   ,令 ( ) e 2ah a a  , ( ) e 2ah a   ， 1a  , ( ) 0h a  ,  ( ) (1) e 2 0h a h     2 eaa  , (e ) 0af   , 所以 ( )f x 在 1(0,e )a 上有且只有一个零点. …………………………………5 分 综上： 当 1a  时，函数无零点. 当 1a  时，函数有且只有一个零点. 当 1a  时，函数有两个零点. ………………………………6 分 （2）由（1）知：当 1a  时， ( ) 0f x  ， 1ln 1x x   ,  1 1 22ln 1 22 1 1 n n n n n a aa a a       , ………………………………7 分  1 11 1 1 2 2 2 n n n n a a a a    ， ………………………………8 分  1 1 1 11 ( 1)2n na a    ， ………………………………9 分  2 1 1 2 1 1 1 1 1 1 1 1 11 ( 1) ( 1) ( 1)2 2 2 2n n n n na a a a             ，  1 1 12n na   ， ………………………………10 分  1 2 1 11 ( )1 1 1 12 2+ 1 ( ) 11 21 2 n n n n n na a a              . …………………………12 分 22.（12 分） 解:（1）根据题意， x 在 70,100 内，按组距为5可分成 6 个小区间， 分别是           70,75 , 75,80 , 80,85 , 85,90 , 90,95 , 95,100 . ………………………1 分 70 100x  ， 由5 5( 1)n x n   , n N ， 14,15,16,17,18,19.n  ………………………2 分 每个小区间的频率值分别是 5P Y  8 109 14,15,1660 1 5 17,18,193 20 n n k nn        …………………3 分  3 11 19 1 11 5 ( 1) 160 60 60 3 2k       ， 3 50k  , n 的所有取值为14,15,16,17,18,19. 3 50k  . …………………………4 分 （2）（ⅰ）由于参赛选手很多，可以把频率视为概率. 由（1）知， B 的分数属于区间           70,75 , 75,80 , 80,85 , 85,90 , 90,95 , 95,100 的概率分别是： 3 11 19 14 11 2, , , , ,60 60 60 60 60 60 . ………………………………5 分 用符号 ijA （或 ijB )表示 A （或 B ）在第一轮获奖等级为i ，通过附加赛最终获奖等级为 j ， 其中 ( , 1,2,3)j i i j  . ………………………………6 分 记“ B 最终获奖等级不低于 A 的最终获奖等级”为事件W ， 则 1 21 22 22 32 22( ) ( )P W P B B B A B A    1 21 22 22 32 22( ) ( ) ( ) ( ) ( ) ( )P B P B P B P A P B P A    2 11 1 11 10 10 14 1 10 51 60 60 11 60 11 11 60 7 11 220           . ………………………………8 分 （ⅱ） A 最终获得一等奖的概率是 21 1( ) 11P A  ，记“第一轮比赛获奖”为事件C , B 最终获得一等奖的概率是 1 21 2 11 1 2 1 160 60( | | ) 27 27 11 27 27 9 60 60 P B C B C       ， 1 1 80( 0) (1 ) (1 )11 9 99P        ， 1 1 1 1 18( 1) (1 ) (1 )11 9 11 9 99P          ， 1 1 1( 2) 11 9 99P      . ……………………………………10分  的分布列为： 80 18 1 20( ) 0 1 +2 =99 99 99 99E       . ……………………………12 分  0 1 2 P 80 99 18 99 1 99