【数学】2020届一轮复习人教版（理）第2章第3讲函数的奇偶性与周期性作业 6页

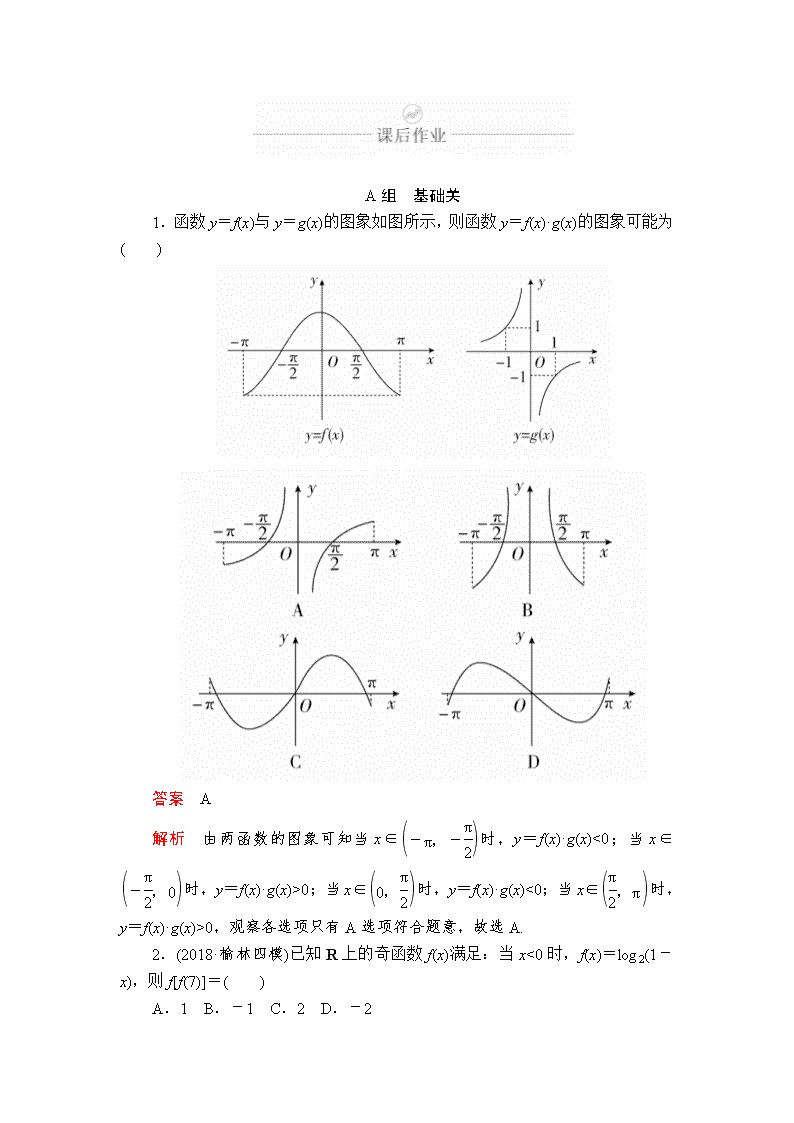
A组　基础关 ‎1．函数y＝f(x)与y＝g(x)的图象如图所示，则函数y＝f(x)·g(x)的图象可能为(　　)‎ 答案　A 解析　由两函数的图象可知当x∈时，y＝f(x)·g(x)<0；当x∈时，y＝f(x)·g(x)>0；当x∈时，y＝f(x)·g(x)<0；当x∈时，y＝f(x)·g(x)>0，观察各选项只有A选项符合题意，故选A.‎ ‎2．(2018·榆林四模)已知R上的奇函数f(x)满足：当x<0时，f(x)＝log2(1－x)，则f[f(7)]＝(　　)‎ A．1 B．－‎1 C．2 D．－2‎ 答案　C 解析　由题意得，f(7)＝－f(－7)＝－log28＝－3，f[f(7)]＝f(－3)＝log24＝2.‎ ‎3．已知f(x)为定义在R上周期为2的奇函数，当－1≤x<0时，f(x)＝x(ax＋1)，若f＝－1，则a＝(　　)‎ A．6 B．‎4 C．－ D．－6‎ 答案　A 解析　因为f(x)是周期为2的奇函数，所以f＝f＝－f＝－＝－1，解得a＝6.‎ ‎4．设函数y＝f(x)，x∈R，“y＝|f(x)|是偶函数”是“y＝f(x)的图象关于原点对称”的(　　)‎ A．充分不必要条件 B．充要条件 C．必要不充分条件 D．既不充分也不必要条件 答案　C 解析　设f(x)＝x2，y＝|f(x)|是偶函数，但是不能推出y＝f(x)的图象关于原点对称．反之，若y＝f(x)的图象关于原点对称，则y＝f(x)是奇函数，这时y＝|f(x)|是偶函数，故选C.‎ ‎5．已知函数y＝f(x)＋x是偶函数，且f(2)＝1，则f(－2)＝(　　)‎ A．2 B．‎3 C．4 D．5‎ 答案　D 解析　∵y＝f(x)＋x是偶函数，∴f(－x)＋(－x)＝f(x)＋x，‎ ‎∴f(－x)＝f(x)＋2x，令x＝2，则f(－2)＝f(2)＋4＝5，故选D.‎ ‎6．(2018·湖南长沙长郡中学模拟)已知f(x)是定义在[－2b,1＋b]上的偶函数，且在[－2b,0]上为增函数，则f(x－1)≤f(2x)的解集为(　　)‎ A. B. C．[－1,1] D. 答案　B 解析　∵f(x)是定义在[－2b,1＋b]上的偶函数，‎ ‎∴－2b＋1＋b＝0，∴b＝1，‎ ‎∵函数f(x)在[－2b,0]上为增函数，‎ ‎∴函数f(x)在[－2,0]上为增函数，‎ 故函数f(x)在[0,2]上为减函数，‎ 则由f(x－1)≤f(2x)，可得|x－1|≥|2x|，‎ 即(x－1)2≥4x2，求得－1≤x≤，‎ 又因为所以－1≤x≤.‎ 故f(x－1)≤f(2x)的解集为.‎ ‎7．(2019·四川成都五校联考)设函数f(x)是奇函数，且在(0，＋∞)上是增函数，又f(－3)＝0，则f(x)<0的解集是(　　)‎ A．{x|－33}‎ B．{x|x<－3或03}‎ D．{x|－33时，f(x)>0.‎ ‎∵函数f(x)是奇函数，∴当－30；当x<－3时，f(x)<0.‎ 则不等式f(x)<0的解集是{x|00，f(－x)＝(－x)3＋ln (1－x)，因为f(x)是R上的奇函数，所以f(x)＝－f(－x)＝－[(－x)3＋ln (1－x)]，所以当x<0时，f(x)＝x3－ln (1－‎ x)．‎ ‎10．已知f(x)是定义在R上的偶函数，并且f(x＋3)＝－，当10在[－1,3]上的解集为(　　)‎ A．(1,3) B．(－1,1)‎ C．(－1,0)∪(1,3) D．(－1,0)∪(0,1)‎ 答案　C 解析　若x∈[－2,0]，则－x∈[0,2]，‎ ‎∵当x∈[0,2]时，f(x)＝x－1，‎ ‎∴f(－x)＝－x－1，∵f(x)是偶函数，‎ ‎∴f(－x)＝－x－1＝f(x)，‎ 即当x∈[－2,0]时，f(x)＝－x－1，‎ 即在一个周期[－2,2]内，‎ f(x)＝ 若x∈[2,4]，则x－4∈[－2,0]，‎ 即f(x)＝f(x－4)＝－(x－4)－1＝－x＋3，x∈[2,4]，‎ 作出函数f(x)在[－2,4]上的图象如图：‎ 则当x∈[－1,3]时，不等式xf(x)>0等价为 或 即10时，满足f(x)＝则f(1)＋f(2)＋f(3)＋…＋f(2020)＝(　　)‎ A．log25 B．－log‎25 C．－2 D．0‎ 答案　B 解析　由题意得f(1)＝－log25，f(2)＝f(－1)＝－f(1)＝log25，f(3)＝f(0)＝0，f(4)＝f(1)，f(5)＝f(2)，f(6)＝f(3)，…，‎ 因为2020＝673×3＋1，所以f(2020)＝f(1)，‎ 所以f(1)＋f(2)＋f(3)＋…＋f(2020)‎ ‎＝[f(1)＋f(2)＋f(3)]×673＋f(1)‎ ‎＝f(1)＝－log25.‎ ‎3．已知函数f(x)是定义在R上的奇函数，且当x>0时，f(x)＝－x2＋ax－1－a，若函数f(x)为R上的单调减函数，则a的取值范围是(　　)‎ A．a≥－1 B．－1≤a≤0‎ C．a≤0 D．a≤－1‎ 答案　B 解析　因为函数f(x)是定义在R上的奇函数，所以f(0)＝0，若函数f(x)为R上的单调减函数，则满足当x>0时，函数为减函数，且当x＝0时，－1－a≤0，‎ 此时即即－1≤a≤0.‎ ‎4．(2018·山东临沂联考)函数f(x)＝－的最大值是M，最小值是m，则f(M＋m)的值等于(　　)‎ A．0 B．2π C．π D. 答案　D 解析　设h(x)＝，则h(－x)＝－h(x)，所以h(x)是一个奇函数，所以函数h(x)的最大值和最小值的和是0，所以M＋m＝π，所以f(M＋m)＝.‎ ‎5．若f(x)＝ln (e3x＋1)＋ax是偶函数，则a＝________.‎ 答案　－ 解析　因为f(x)＝ln (e3x＋1)＋ax是偶函数，所以f(－x)＝f(x)，所以f(－x)＝ln (e－3x＋1)－ax＝ln －ax＝ln －ax＝ln (1＋e3x)－3x－ax＝ln (e3x＋1)＋ax，所以－3－a＝a，解得a＝－.‎ ‎6．定义在实数集R上的函数f(x)满足f(x)＋f(x＋2)＝0，且f(4－x)＝f(x)．现有以下三个命题：‎ ‎①8是函数f(x)的一个周期；②f(x)的图象关于直线x＝2对称；③f(x)是偶函数．‎ 其中正确命题的序号是________．‎ 答案　①②③‎ 解析　由f(x)＋f(x＋2)＝0可得f(x＋4)＝－f(x＋2)＝f(x)，‎ ‎∴函数f(x)的周期是4，①正确；‎ 由f(4－x)＝f(x)，可得f(2＋x)＝f(2－x)，f(x)的图象关于直线x＝2对称，②正确；f(4－x)＝f(－x)且f(4－x)＝f(x)，‎ ‎∴f(－x)＝f(x)，f(x)为偶函数，③正确．‎