江苏省七市（南通、泰州、扬州、徐州、淮安、连云港、宿迁）2020届高三下学期第三次调研考试数学试题 Word版含解析 27页

- 1 - 江苏省苏北七市 2020 届高三第三次调研考试 数学试题 一、填空题（本大题共 14 小题，每小题 5 分，共计 70 分．不需要写出解答过程，请将答案 填写在答题卡相应的位置上．．．．．．．．．．） 1. 已知集合 A＝{﹣1，0，1}，B＝{0，2}，则 A  B＝_______． 【答案】{﹣1，0，1，2} 【解析】 【分析】 直接利用集合的并集运算求解. 【详解】解：∵集合 A＝{﹣1，0，1}，B＝{0，2}， ∴A  B＝{﹣1，0，1，2}． 故答案为：{﹣1，0，1，2} 【点睛】本题主要考查集合的并集运算，意在考查学生对该知识的理解掌握水平，属于基础 题. 2. 设复数 z 满足(3﹣i)z＝ 10 ，其中 i 为虚数单位，则 z 的模是_______． 【答案】1 【解析】 【分析】 先利用复数的除法求出复数 z ，再求复数的模得解. 【详解】解：∵(3﹣i)z＝ 10 ，∴ 10 10(3 ) 3 10 10 3 10 10 i3 (3 )(3 ) 10 10 10 i iz i i i         ， ∴ 2 23 10 10( ) ( ) 110 10z    ． 故答案为：1 【点睛】本题主要考查复数的除法运算和复数模的计算，意在考查学生对这些知识的理解掌 握水平，属于基础题. 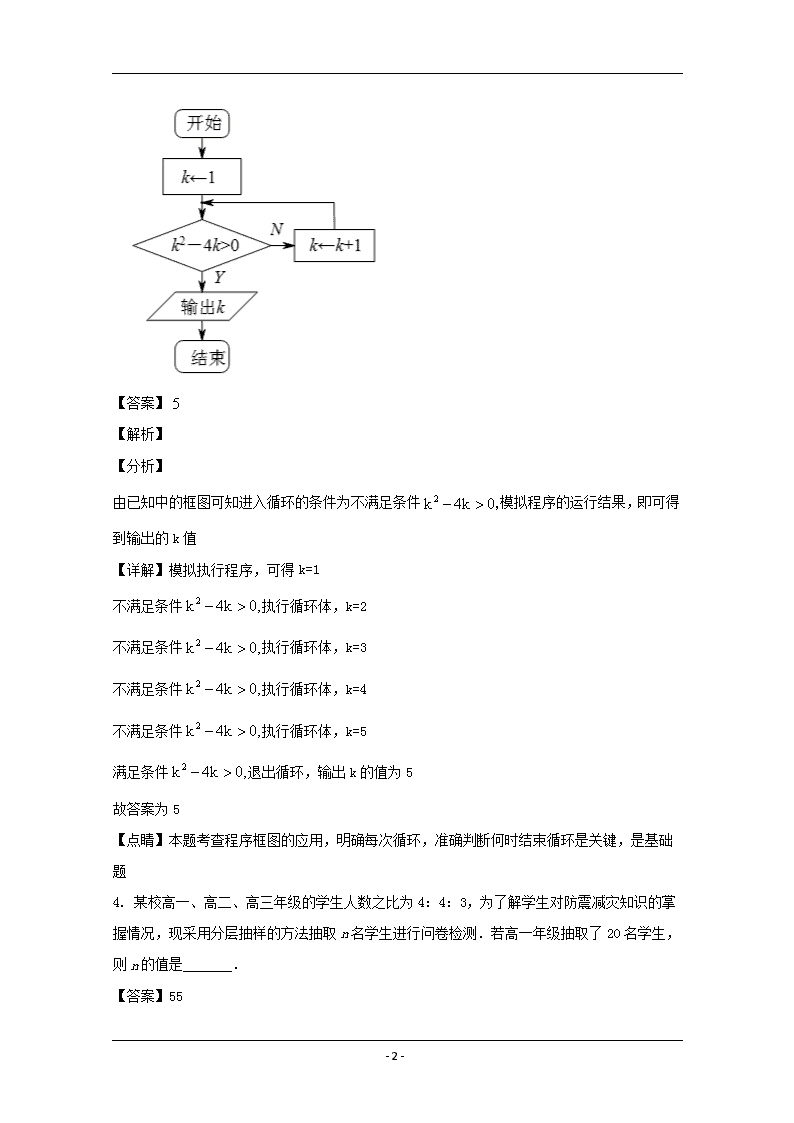3. 如图是一个算法流程图，则输出的 k 的值是____． - 2 - 【答案】 5 【解析】 【分析】 由已知中的框图可知进入循环的条件为不满足条件 2k 4k 0，  模拟程序的运行结果，即可得 到输出的 k 值 【详解】模拟执行程序，可得 k=1 不满足条件 2k 4k 0,  执行循环体，k=2 不满足条件 2k 4k 0,  执行循环体，k=3 不满足条件 2k 4k 0,  执行循环体，k=4 不满足条件 2k 4k 0,  执行循环体，k=5 满足条件 2k 4k 0,  退出循环，输出 k 的值为 5 故答案为 5 【点睛】本题考查程序框图的应用，明确每次循环，准确判断何时结束循环是关键，是基础 题 4. 某校高一、高二、高三年级的学生人数之比为 4：4：3，为了解学生对防震减灾知识的掌 握情况，现采用分层抽样的方法抽取 n 名学生进行问卷检测．若高一年级抽取了 20 名学生， 则 n 的值是_______． 【答案】55 - 3 - 【解析】 【分析】 根据分层抽样每个个体入样的可能性相同，计算可得； 【详解】解：依题意可得 20 (4 4 3) 554     ． 故答案为：55 【点睛】本题考查分层抽样的应用，属于基础题. 5. 今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果, 功不可没.“三药” 分别为金花清感颗粒、连花清瘟胶囊、血必净注射液；“三方”分别为清肺排毒汤、化湿败 毒方、宜肺败毒方,若某医生从“三药三方”中随机选出 2 种,则恰好选出 1 药 1 方的概率是 _______. 【答案】 3 5 【解析】 【分析】 根据组合的方法结合古典概型的概率公式求解即可. 【详解】从“三药三方”中随机选出 2 种共 2 6 15C  个基本事件,其中 1 药 1 方的事件数有 1 1 3 3 9C C  个.故概率 P＝ 9 3 15 5  . 故答案为： 3 5 【点睛】本题主要考查了利用组合的方法解决随机事件的概率问题,属于基础题. 6. 在平面直角坐标系 xOy 中,已知抛物线 y2＝4x 的准线是双曲线 2 2 2 12 x y a   (a＞0)的左准线, 则实数 a 的值是_______． 【答案】 2 【解析】 【分析】 根据抛物线以及双曲线的准线方程列式求解即可. 【详解】因为抛物线 y2＝4x 的准线是双曲线 2 2 2 12 x y a   (a＞0)的左准线,故 2 2 1 2 a a     , - 4 - 即   2 4 2 22 2 1 0a a a a      ,因为 0a  故解得 a＝ 2 ． 故答案为： 2 【点睛】本题主要考查了抛物线与双曲线的简单性质,属于基础题. 7. 已知 5cos( ) 13    ， 3sin 5   ， ，  均为锐角，则sin 的值是_______． 【答案】 33 65 【解析】 【分析】 计算得到 12sin( ) 13    ， 4cos 5   ，再利用和差公式计算得到答案. 【详解】∵ ，  均为锐角，∴  0,    ，从而sin( ) 0   ， cos 0  ， ∵ 5cos( ) 13    ， 3sin 5   ，∴ 12sin( ) 13    ， 4cos 5   ， ∴sin sin[( ) ] sin( )cos cos( )sin                12 4 5 3 33 13 5 13 5 65      . 故答案为： 33 65 . 【点睛】本题考查了三角恒等变换，意在考查学生的计算能力和转化能力. 8. 公园里设置了一些石凳供游客休息,这些石凳是经过正方体各棱的中点截去 8 个一样的四 面体得到的（如图所示）．设石凳的体积为 V1,正方体的体积为 V2,则 1 2 V V 的值是_______． 【答案】 5 6 - 5 - 【解析】 【分析】 设正方体的棱长为 2a 即可得出 V2,再利用总体积减去正方体八个角上的三棱锥的体积求出 V1, 继而得出 1 2 V V 即可. 【详解】解析：设正方体的棱长为 2a, 则 V2＝8a3, 2 3 3 3 1 2 1 1 4 208 83 2 3 3V V a a a a a        , 故 3 1 3 2 20 53 8 6 aV V a   ． 【点睛】本题主要考查了空间几何体的体积问题,属于基础题. 9. 已知 x＞1，y＞1，xy＝10，则 1 4 lg lgx y  的最小值是_______． 【答案】9 【解析】 【分析】 依题意可得 lg lg 1x y  ，再由基本不等式计算可得； 【详解】解：∵ 10xy  , 1x  , 1y  ，∴ lg lg 1x y  ， lg 0x  ， lg 0y ， 所以 1 4 1 4 lg 4lg lg 4lg( )(lg lg ) 5 5 2lg lg lg lg lg lg lg lg y x y xx yx y x y x y x y           5 2 4 9   ，当且仅当 lg 4lg lg lg y x x y  ，即 1 310x  时取“＝”． 故答案为：9 【点睛】本题考查对数的运算及基本不等式的应用，属于基础题. 10. 已知等比数列 na 的前 n 项和为 nS ,若 24S , 4S , 32S 成等差数列,且 2 3 2a a  ,则 6a 的值是_______． 【答案】 32 【解析】 - 6 - 【分析】 根据等差等比数列的性质列式求解得 2q   ,再利用等比数列各项的关系求解 6a 即可. 【详解】∵ 24S , 4S , 32S 成等差数列,∴ 4 2 32 4 2S S S  ,即 4 2 2 3S S S S   , 所以 3 4 3a a a   ,故 4 3 2a a   .∴ 2q   . 又 2 3 2a a  ,则  2 1 2 2a   ,所以 2 2a   , 4 6 2 32a a q   ． 故答案为： 32 【点睛】本题主要考查了等比数列的简单性质,等差中项的运用等,属于基础题. 11. 海伦（Heron，约公元 1 世纪）是古希腊亚历山大时期的数学家，以他的名字命名的“海 伦公式”是几何学中的著名公式，它给出了利用三角形的三边长 a，b，c 计算其面积的公式 S△ABC＝ ( )( )( )p p a p b p c   ，其中 2 a b cp   ，若 a＝5，b＝6，c＝7，则借助“海伦 公式”可求得△ABC 的内切圆的半径 r 的值是_______． 【答案】 2 6 3 【解析】 【分析】 首先根据海伦公式求得三角形 ABC 的面积，然后根据三角形内切圆计算公式，计算出三角形 ABC 的内切圆. 【详解】 5 6 7 92 2 a b cp       ，S△ABC＝ 9 (9 5) (9 6) (9 7) 6 6       ， 由于  1 2ABCS a b c r     ，所以 2 2 6 6 2 6 5 6 7 3 Sr a b c       ． 故答案为： 2 6 3 【点睛】本小题主要考查三角形面积的计算，考查三角形内切圆半径的计算，属于基础题. 12. 如图,△ABC 为等边三角形,分别延长 BA,CB,AC 到点 D,E,F,使得 AD＝BE＝CF．若 BA 2AD  ,且 DE＝ 13 ,则 AF CE  的值是_______． - 7 - 【答案】 9 2  【解析】 【分析】 设 AD＝x,再在△BDE 中根据余弦定理求解得出 1x  ,再利用数量积公式求解 AF CE  即可. 【详解】易知△DEF 也为等边三角形,设 AD＝x,则 BD＝3x, △BDE 中,由余弦定理得：    2 2 113 3 2 3 2x x x x         ,解得 x＝1, 故 BD＝3,则 9AF CE 3 3 cos120 2         ． 故答案为： 9 2  【点睛】本题主要考查了平面向量数量积以及余弦定理的运用,属于基础题. 13. 已知函数 2 2(1 ), 0( ) 2 , 0 k xf x x x k x        ,若函数 ( ) ( ) ( )g x f x f x   有且仅有四个不同的零 点,则实数 k 的取值范围是_______． 【答案】  27, 【解析】 【分析】 根据题意可求得 2 2 2 , 0 ( ) 4 , 0 2 , 0 kx k xx g x k x kx k xx              ,再分 0, 0, 0k k k   三种情况求函数的单调 性,进而根据零点存在性定理求出函数的最小值求解不等式即可. - 8 - 【详解】由题,   2 2 21 2 , 0 ( ) 2 2 , 0 22 1 , 0 k x k xx g x k k x x k k xx                        ,即 2 2 2 , 0 ( ) 4 , 0 2 , 0 kx k xx g x k x kx k xx              , 当 k＝0 时,原函数有且只有一个零点,不符题意,故 k≠0, 观察解析式,可知函数 ( )g x 有且仅有四个不同的零点, 可转化为 2 2( ) , 0kg x x k xx     有且仅有两个不同的零点, 当 k＜0,函数 ( )g x 在(0,  )单调递增,最多一个零点,不符题意,舍； 当 k＞0, 3 2 2( )( ) , 0x kg x xx    , 令 ( ) 0g x  有 1 3x k ,故 x (0, 1 3k ) 1 3k ( 1 3k ,  ) ( )g x ﹣ 0 ﹢ ( )g x 单调递减 单调递增 要使 ( )g x 在(0,  )有且仅有两个不同的零点, 则 1 2 3 3 min 1 3 2( ) ( ) 0kg x g k k k k      ,因为 0k  ,故 2 1 3 33 3k k k   ,解得 k＞27, 综上所述,实数 k 的取值范围是(27,  )． 故答案为：(27,  ) 【点睛】本题主要考查了根据分段函数的零点个数求解参数范围问题,需要根据函数的性质求 出单调性以及最值,进而根据零点存在性定理列式求解.属于中档题. 14. 在平面直角坐标系 xOy 中，过点 P(2，﹣6)作直线交圆 O：x2＋y2＝16 于 A，B 两点， C( 0x ， 0y )为弦 AB 的中点，则 2 2 0 0( 1) ( 3)x y   的取值范围是_______． - 9 - 【答案】[ 10 ， 42 ) 【解析】 【分析】 求出点 C 的轨迹，转化条件 2 2 0 0( 1) ( 3)x y   为点 C( 0x ， 0y )到点  1,3Q  距离，数形 结合即可得解. 【详解】因为 C( 0x ， 0y )为弦 AB 的中点，所以OC PC ， 圆 O：x2＋y2＝16 的圆心为  0,0O ，半径为 4 ， 所以 4 36 2 10OP    ， OP 的中点  1, 3T  ， C 在以 OP 为直径的圆即圆 2 2:( 1) ( 3) 10T x y    上，且 C 在圆 O 内，如图所示，圆T 上的 劣弧 EF （不含端点）即为 C 的轨迹， 2 2 0 0( 1) ( 3)x y   可转化为点 C( 0x ， 0y )到点  1,3Q  距离， 由图可知， min 10 10CQ TQ   , - 10 - 联立方程    2 2 2 2 1 3 10 16 x y x y        可得 4 6 6 5 12 2 6 5 x y      或 4 6 6 5 12 2 6 5 x y      ， 所以点 4 6 6 12 2 6,5 5E        ， 4 6 6 12 2 6,5 5F        ， 所以 2 24 6 6 12 2 6( 1) ( 3) 425 5EQ FQ        ， 所以 2 2 0 0( 1) ( 3)x y   的取值范围是[ 10 ， 42 )． 故答案为：[ 10 ， 42 ). 【点睛】本题考查了直线与圆的综合应用，考查了数形结合思想与转化化归思想，属于中档 题. 二、解答题（本大题共 6 小题，共计 90 分．请在答题纸指定区域．．．．．．．内作答，解答应写出文字说 明，证明过程或演算步骤．） 15. △ABC 中，角 A，B，C 所对的边分别为 a，b，c．若 5(sinC sin B) 5sin A 8sin B a b c    ． （1）求 cosC 的值； （2）若 A＝C，求 sinB 的值． 【答案】（1） 4 5 （2） 24 25 【解析】 【分析】 （1）利用正弦定理将角化边，再由余弦定理计算可得； （2）由（1） 4cos 5C  ，由同角三角函数的基本关系求出sinC ，再由诱导公式及二倍角公 式计算可得； 【详解】解：（1）由正弦定理： sin sin sin a b c A B C   ，且 5(sinC sin B) 5sin A 8sin B a b c    得 5( ) 5 8c b a b a b c    ， - 11 - 整理得：  2 2 25 8a b c ab   ，故由余弦定理： 2 2 2 4cos 2 5 a b cC ab    ； （2）由（1） 4cos 5C  ，又 C 为△ABC 内角，故 2 3sin 1 cos 5C C   ， A C ，则 24sin sin( ) sin( ) sin 2 2sin cos 25B A C A C C C C        ． 【点睛】本题考查正弦定理、余弦定理的应用，同角三角函数的基本关系，属于基础题. 16. 如图,在直三棱柱 ABC—A1B1C1 中,AC⏊BC,D,E 分别是 A1B1,BC 的中点．求证： （1）平面 ACD⊥平面 BCC1B1； （2）B1E∥平面 ACD． 【答案】（1）见解析（2）见解析 【解析】 【分析】 (1)根据直三棱柱的性质,证明 1,AC BC AC CC  进而得到 AC  平面 1 1BCC B 即可. (2) 取 AC 中点 F,连结 EF,DF,再证明四边形 B1DFE 为平行四边形即可. 【详解】证明：（1）直三棱柱 ABC—A1B1C1 中,CC1⊥底面 ABC,又 AC 底面 ABC 故 AC⊥CC1,又因为 AC⊥BC,CC1∩BC＝C CC1  平面 BCC1B1,BC 平面 BCC1B1 所以,AC⊥平面 BCC1B1,又因为 AC  平面 ACD 所以,平面 ACD⊥平面 BCC1B1； （2）取 AC 中点 F,连结 EF,DF 因为 E,F 分别为 BC,AC 中点 所以,EF∥AB,EF＝ 1 2 AB - 12 - 三棱柱 ABC—A1B1C1 中,AB// A1B1,AB＝A1B1 又因为 D 为 A1B1 中点,所以 B1D∥AB,B1D＝ 1 2 AB 所以,EF∥B1D,EF＝B1D 因此,四边形 B1DFE 为平行四边形 所以 B1E//DF,又因为 DF 平面 ACD,B1E  平面 ACD 所以,B1E∥平面 ACD． 【点睛】本题主要考查了根据线面垂直与平行的性质证明面面垂直以及线面垂直等,属于中档 题. 17. 某单位科技活动纪念章的结构如图所示，O 是半径分别为 1cm，2cm 的两个同心圆的圆心， 等腰△ABC 的顶点 A 在外圆上，底边 BC 的两个端点都在内圆上，点 O，A 在直线 BC 的同侧．若 线段 BC 与劣弧 BC 所围成的弓形面积为 S1，△OAB 与△OAC 的面积之和为 S2， 设∠BOC＝2 ． （1）当 3   时，求 S2﹣S1 的值； （2）经研究发现当 S2﹣S1 的值最大时，纪念章最美观，求当纪念章最美观时，cos 的值．（求 导参考公式：(sin2x)'＝2cos2x，(cos2x)'＝﹣2sin2x） 【答案】（1） 5 3 4 3  ( 2cm )；（2） 1 5 2   【解析】 - 13 - 【分析】 依题意可得 2 (0, )BOC     ，故 (0, )2   ， 1 sin cosS     ， 2 2sinS  ， （1）当 3   时，代入计算可得； （2）由 2 1 12sin sin 22S S       ， (0, )2   令 1( ) 2sin sin 22f       ， (0, )2   ，利用导数研究函数的单调性，求出函数的最值； 【详解】解：过点 O 作OD BC^ 于点 D ，则 D 为 BC 的中点，又 ABC 为等腰三角形，所 以 A 、O 、 D 三点共线， BOA AOC       2 (0, )BOC     ，故 (0, )2   1 1 12 1 1 sin 2 sin cos2 2S OB OC             2 12 1 2sin 2sin2S         （1） 3   时， 1 3 3 4S   ， 2 3S  ，故 2 1 5 3 4 3S S    ， 答：当 3   时，求 2 1S S 的值为 5 3 4 3  ( 2cm )； （2） 2 1 12sin sin 22S S       ， (0, )2   令 1( ) 2sin sin 22f       ， (0, )2   2( ) 2cos 2cos 2f       - 14 - 令 ( ) 0f   ，得 1 5cos 2    或 1 5cos 2    （舍去） 记 0 1 5cos 2    ， 0 (0, )2     00, 0 0 , 2      ( )f  ＋ 0 － ( )f  单调递增 极大值 单调递减 故 0=  ，即 1 5cos 2    时， ( )f  最大，即 2 1S S 的值最大， 答：纪念章最美观时，cos 的值为 1 5 2   ． 【点睛】本题考查利用导数研究函数的最值，三角形面积公式的应用，属于中档题. 18. 如图，在平面直角坐标系 xOy 中，已知椭圆 2 2 2 2 1x y a b   (a＞b＞0)的左、右焦点分别为 F1，F2，过点 F2 的直线交椭圆于 M，N 两点．已知椭圆的短轴长为 2 2 ，离心率为 6 3 ． - 15 - （1）求椭圆的标准方程； （2）当直线 MN 的斜率为 5 时，求 1 1| | | |F M F N 的值； （3）若以 MN 为直径的圆与 x 轴相交的右交点为 P(t，0)，求实数 t 的取值范围． 【答案】（1） 2 2 16 2 x y  （2）13 6 4 （3） 6[ 6,2 ]3t   ． 【解析】 【分析】 （1）设焦距 2c，由题得到关于 , ,a b c 的方程组，解方程组即得解； （2）先求出点 ,M N 的坐标，再利用两点间的距离公式得解； （3）先讨论当直线 MN 斜率不存在时， 62 3t   ；再讨论直线 MN 斜率存在的情况,联立直 线和椭圆方程得到韦达定理，再根据 0PM PN   得到 2 2 2 (6 )(3 12 10) 0 t t t t       ，解不等 式组综合即得解. 【详解】解：（1）设焦距 2c， 2 2 2 2 2 2 2 6 6 3 b b a c a c a           ， 2b  ， 故椭圆的标准方程为： 2 2 16 2 x y  ； （2）由（1）知，c＝2，则 F2(2，0) 2 2 9 5( 2) 4 3 6 5 4 xy x x y y          或 3 2 5 2 x y      即 9 5 3 5( , ), ( , )4 4 2 2M N  ，或 9 5 3 5( , ), ( , )4 4 2 2N M  ， - 16 - 因此， 2 2 2 2 1 1 9 5 3 5 13 6| | | | ( 2 ) (0 ) ( 2 ) (0 )4 4 2 2 4F M F N            ； （3）当直线 MN 斜率不存在时，MN：x＝2，| |MN ＝ 2 6 3 ， 以 MN 为直径的圆方程为： 2 2 2( 2) 3x y   , 其与 x 轴相交的右交点为( 62 3  ，0)，即 62 3t   ； 当 MN 的斜率存在时，设 MN： ( 2)y k x  ，M( 1x ， 1y )，N( 2x ， 2y ) 2 2 2 2 2 2 ( 2) (3 1) 12 12 6 03 6 y k x k x k x kx y           ， 所以 224( 1)k   ， 2 1 2 2 12 3 1 kx x k    ， 2 1 2 2 12 6 3 1 kx x k   ， 则 2 2 1 2 1 2 1 2 1 2 2 2( 2) ( 2) [ 2( ) 4] 3 1 ky y k x k x k x x x x k           ， 因为 P 在以 MN 为直径的圆上，则 0PM PN    ， 所以 1 2 1 2( )( ) 0x t x t y y    所以 2 1 2 1 2 1 2( ) 0x x t x x t y y     所以 2 2 2 2 2 2 2 12 6 12 2 03 1 3 1 3 1 k k kt tk k k         所以 2 2 2(3 12 10) 6t t k t    ， 因为 23 12 10 0t t   ， 所以 2 2 2 6 3 12 10 tk t t    . ∵P 是右交点，故 t＞2， - 17 - 因此 2 2 2 (6 )(3 12 10) 0 t t t t       ， 解得 6[ 6,2 ]3t   ． 综合得 6[ 6,2 ]3t   . 【点睛】本题主要考查椭圆标准方程的求法，考查直线和椭圆的位置关系，考查椭圆中的范 围问题的求解，意在考查学生对这些知识的理解掌握水平和分析推理计算能力. 19. 已知 na 是各项均为正数的无穷数列，数列 nb 满足 n n n kb a a   (n N )，其中常数 k 为正整数． （1）设数列 na 前 n 项的积 ( 1) 22 n n nT   ，当 k＝2 时，求数列 nb 的通项公式； （2）若 na 是首项为 1，公差 d 为整数的等差数列，且 2 1b b ＝4，求数列 1 nb       的前 2020 项的和； （3）若 nb 是等比数列，且对任意的 n N ， 2 2n n k n ka a a   ，其中 k≥2，试问： na 是 等比数列吗？请证明你的结论． 【答案】（1） 4n nb = ；（2） 2020 2020 2021S  （3）数列 na 是等比数列．证明见解析 【解析】 【分析】 （1）先求出 12 ( )n na n N   ，即得数列 nb 的通项公式； （2）通过分析得到 d＝1，得到 na n ，再求出 k＝1，即得 ( 1)nb n n  ，再利用裂项相消法 求数列 1 nb       的前 2020 项的和； （3）设 nb 公比为 q2，则对任意 n N ， 22 kn k n k n k n n n k b a a qb a a       ，由已知得到 kn k n a qa   ， - 18 - 证明得到 1n n a qa   ，即得数列 na 是等比数列． 【详解】解：（1）因为 ( 1) 22 n n nT   ，所以 ( 2)( 1) 2 1 2 ( 2) n n nT n      ， 两式相除，可得 ( 1) ( 1)( 2) 122 2 ( 2) n n n n n na n        ， 当 n＝1 时， 1 1 1 1 1 2a T    ，符合上式，所以 12 ( )n na n N   ， 当 k＝2 时， 1 1 2 2 2 4n n n n n nb a a        ； （2）因为 n n n kb a a   ，且 1 1a  ， 所以 1 1 1 1k kb a a a   ， 2 2 2 1( 1)( )k kb a a d a d     ， 所以 2 2 1 1( 1) 4kb b d d a      ， 因为 na 是各项均为正数的无穷数列， na 是首项为 1，公差 d 为整数的等差数列， 所以 d，k 均为正整数，所以 1d  ，所以 1 2 1 2ka a d     ， 所以 2 2 1( 1) 4 3kd d a d d     ，解得 d≤1，所以 d＝1，即 na n . 所以 2 1 1( 1) 4 2k kd d a a      ，即 1 2ka   ，解得 k＝1， 所以 1 ( 1)n n nb a a n n   ，则 1 1 1 1nb n n    ， 记 nb 的前 n 项和为 nS ， 则 1 1 1 1 1 1 1 11 ( ) ( ) ( ) 12 2 3 3 4 1 1nS n n n             ， 所以 2020 1 20201 2021 2021S    ； （3）因为 nb 成等比数列，设公比为 q2，则对任意 n N ， 22 kn k n k n k n n n k b a a qb a a       ， 因为 0na  ，且 2 2n n k n ka a a   ，所以 2n k n k n n k a a a a     ，所以 kn k n a qa   ， 因为 2 2 21 1 1 1 1 2 ( ) k n n n k n n k n n n k n n b a a a q a qb a a a q a            ，所以 1n n a qa   ， - 19 - 所以数列 na 是等比数列． 【点睛】本题主要考查数列通项的求法，考查数列的求和问题，考查数列性质的判定，意在 考查学生对这些知识的理解掌握水平和分析推理能力. 20. 已知函数 ln( ) a xf x x  ， ln( ) x x ag x e  ，其中 e 是自然对数的底数． （1）若函数 ( )f x 的极大值为 1 e ，求实数 a 的值； （2）当 a＝e 时，若曲线 ( )y f x 与 ( )y g x 在 0x x 处的切线互相垂直，求 0x 的值； （3）设函数 ( ) ( ) ( )h x g x f x  ，若 ( )h x ＞0 对任意的 x(0，1)恒成立，求实数 a 的取值 范围． 【答案】（1）a＝1；（2） 0 1x  ；（3）[ 1 e ，  )． 【解析】 【分析】 （1）利用导数求出 ( )f x 的极大值 1( ) af e e e   ，即得 a 的值； （2）由 0 0( ) ( ) 1f x g x    得到 0 0 0lnxx e e x e  ，设 ( ) lnxx xe e x   ，根据函数的单调 性和 (1) e  得到 0 1x  ； （3）由题得 ln( ) lnx x ae x ae x  对任意 x(0，1)恒成立，设 ln( ) xH x x  ，得到 xae x 对任意 x(0，1)恒成立，即 x xa e  ，设 ( ) x xG x e  ，x(0，1)，求出 ( )G x 的最大值得解. 【详解】解：（1）因为 ln( ) a xf x x  ，则 2 (1 ln )( ) a xf x x   ， 因为 ln( ) x x ag x e  ，所以 a＞0， 则当 x(0，e)时， ( ) 0f x  ， ( )f x 单调递增， 当 x(e，  )时， ( ) 0f x  ， ( )f x 单调递减， 所以当 x＝e 时， ( )f x 的极大值 1( ) af e e e   ，解得 a＝1； - 20 - （2）当 a＝e 时， ln( ) e xf x x  ， 1( ) x xg x e  ， 则 2 (1 ln )( ) e xf x x   ， ( ) ex xg x   ， 由题意知， 0 0 0 0 0 2 0 (1 ln )( ) ( ) 1x e x xf x g x x e        ， 整理得 0 0 0lnxx e e x e  ， 设 ( ) lnxx xe e x   ，则 ( ) ( 1) 0x ex x e x      ，所以 ( ) x 单调递增， 因为 (1) e  ，所以 0 1x  ； （3）由题意可知， ln ln( ) 0x x a a xh x e x    对任意 x(0，1)恒成立， 整理得 ln( ) lnx x ae x ae x  对任意 x(0，1)恒成立， 设 ln( ) xH x x  ，由（1）可知， ( )H x 在(0，1)上单调递增， 且当 x(1，  )时， ( ) 0H x  ，当 x(0，1)时， ( ) 0H x  ， 若 1xae x  ，则 ( ) 0 ( )xH ae H x  ， 若 0 1xae  ，因为 ( ) ( )xH ae H x ，且 ( )H x 在(0，1)上单调递增，所以 xae x ， 综上可知， xae x 对任意 x(0，1)恒成立，即 x xa e  ， 设 ( ) x xG x e  ，x(0，1)，则 1( ) 0x xG x e    ，所以 ( )G x 单调递增， 所以 1( ) (1)G x G ae    ，即 a 的取值范围为[ 1 e ，  )． 【点睛】本题主要考查利用导数研究函数的单调性和极值问题，考查利用导数研究不等式的 恒成立问题和最值问题，意在考查学生对这些知识的理解掌握水平和分析推理能力. 江苏省七市 2020 届高三第三次调研考试 数学附加题 【选做题】本题包括 A，B，C 三小题，请选定其中两题作答，每小题 10 分共计 20 分，解答 时应写出文字说明，证明过程或演算步骤． - 21 - 选修 4—2：矩阵与变换 21. 已知 m R ， 1 1       是矩阵 1 2 1M m     的一个特征向量，求 M 的逆矩阵 1M  ． 【答案】 1 1 2 3 3M 2 1 3 3            ． 【解析】 【分析】 根据特征向量定义及矩阵乘法运算，先求得矩阵 M ；设矩阵 M 的逆矩阵 1M a b c d       ，由 矩阵乘法运算可得方程组，解方程组即可确定 M 的逆矩阵 1M  ． 【详解】设 1 1       是属于特征值 n 的一个特征向量，则 M n = ， 因为 1 1 1 2 1 1 3 m mM               ， 1 1 nn n n             ， 所以1 3m n   ，解得 2m  ， 所以矩阵 1 2 2 1      M ， 设矩阵 M 的逆矩阵 1M a b c d       ， 则 1 1 2 2 1 2 2 1 0M 2 2 0 1 a b a c b d c d a c b dM                          所以 2 1 2 0 2 0 2 1 a c b d a c b d           ，解得 1 3 2 3 2 3 1 3 a b c d               ， - 22 - 所以 1 1 2 3 3M 2 1 3 3            ． 【点睛】本题考查了矩阵特征向量的应用，逆矩阵的求法，属于中档题. 选修 4—4：坐标系与参数方程 22. 在极坐标系中，圆C 的方程为  2 sin 0r r   .以极点为坐标原点，极轴为 x 轴正半轴 建立平面直角坐标系，直线 l 的参数方程为 3 1 3 x t y t      （t 为参数）．若直线l 与圆C 恒有公 共点，求 r 的取值范围． 【答案】 2, 【解析】 【分析】 将圆的极坐标方程化为普通方程，确定圆心和半径，并将直线l 的方程化为一般方程，利用圆 心到直线 l 的距离不大于 r 可得出关于 r 的不等式，进而可求得正数 r 的取值范围. 【详解】因为圆C 的极坐标方程为 2 sinr  ，所以 2 2 sinr   ， 因为 2 2 2x y   ， sin y   ，所以 2 2 2x y ry  ，整理得  22 2x y r r   ， 即圆C 是圆心为 0,r ，半径为 r 的圆， 因为直线 l 的参数方程为 3 1 3 x t y t      ，消去t 得 3 2 0x y   ， 所以，直线l 的普通方程为 3 2 0x y   ， 因为直线 l 和圆C 有公共点，所以圆心C 到直线l 的距离 2 2 23 1 r rd r       ，解得 2r  ， 因此， r 的取值范围是 2, . 【点睛】本题考查利用直线与圆的位置关系求参数的取值范围，同时也考查曲线的极坐标方 程、参数方程与普通方程之间的相互转化，考查计算能力，属于中等题. 选修 4—5：不等式选讲 - 23 - 23. 已知 1x  ， 1y  ，且 4x y  ，求证： 2 2 81 1 y x x y    ． 【答案】证明见解析 【解析】 【分析】 设 1x m  ， 1y n  ，可得出 2m n  ，然后利用基本不等式可证得 2 2 81 1 y x x y    . 【 详 解 】 设 1x m  ， 1y n  ， 因 为 1x  ， 1y  ， 所 以 0m  ， 0n  ， 且 2 2m n x y     ，        2 2 2 22 2 2 21 1 4 4 2 16 81 1 n mn my x n m x y m n m n m n             . 当且仅当 1m n  ，即 2x y  时，上述等号成立，原命题得证． 【点睛】本题考查利用基本不等式证明不等式，解答的关键在于对代数式进行化简变形，考 查推理能力与计算能力，属于中等题. 【必做题】每题 10 分，共计 20 分，解答时应写出文字说明，证明过程或演算步骤． 24. 某“芝麻开门”娱乐活动中，共有 5 扇门，游戏者根据规则开门，并根据打开门的数量获 取相应奖励．已知开每扇门相互独立，且规则相同，开每扇门的规则是：从给定的 6把钥匙（其 中有且只有1把钥匙能打开门）中，随机地逐把抽取钥匙进行试开，钥匙使用后不放回．若门 被打开，则转为开下一扇门；若连续 4 次未能打开，则放弃这扇门，转为开下一扇门；直至 5 扇门都进行了试开，活动结束． （1）设随机变量 X 为试开第一扇门所用的钥匙数，求 X 的分布列及数学期望  E X ； （2）求恰好成功打开 4 扇门的概率． 【答案】（1）见解析，   3E X  ；（2） 80 243 ． 【解析】 【分析】 （1）由题意可知，随机变量 X 的可能取值为1、 2 、3 、4 ，计算出随机变量 X 在不同取值 下的概率，可得出随机变量 X 的概率分布列，利用数学期望公式可求得  E X ； （2）计算出每扇门被打开的概率，然后利用独立重复试验的概率公式可求得所求事件的概率. - 24 - 【详解】（1）由题意可知，随机变量 X 的可能取值为1、 2 、 3 、 4 ， 则   11 6P X   ，   5 1 12 6 5 6P X     ，   5 4 1 13 6 5 4 6P X      ，   5 4 3 1 5 4 3 2 14 6 5 4 3 6 5 4 3 2P X           ， 所以随机变量 X 的分布列为： X 1 2 3 4 P 1 6 1 6 1 6 1 2 所以随机变量的数学期望   1 1 1 11 2 3 4 36 6 6 2E X          ； （2）由（1）可知，每扇门被打开的概率为 5 4 3 2 21 6 5 4 3 3P       ， 设恰好成功打开四扇门为事件 A ，则   4 4 5 2 1 80 3 3 243P A C       ． 【点睛】本题考查随机变量及其分布列以及数学期望的计算，同时也考查了独立重复试验概 率的计算，考查计算能力，属于中等题. 25. 如图，在平面直角坐标系 xOy 中，已知抛物线  2 2 0y px p  的焦点为 F ，准线与 x 轴 的交点为 E ．过点 F 的直线与抛物线相交于 A 、 B 两点， EA 、 EB 分别与 y 轴相交于 M 、 N 两点，当 AB x 轴时， 2EA  ． （1）求抛物线的方程； （2）设 EAB 的面积为 1S ， EMN 面积为 2S ，求 1 2 S S 的取值范围． - 25 - 【答案】（1） 2 2 2y x ；（2） 4, ． 【解析】 【分析】 （1）当 AB x 轴时，求出 AF ，利用勾股定理可求得正数 p 的值，进而可得出抛物线的标 准方程； （2）设直线 AB 的方程为 2 2x my  ，设点  1 1,A x y 、  2 2,B x y ，求出点 M 、 N 的坐 标，进而可求得 1S 、 2S 关于 m 的表达式，可得出 1 2 S S 关于 m 的表达式，利用不等式的基本性 质可求得 1 2 S S 的取值范围. 【详解】（1）当 AB x 轴时，直线 AB 的方程为 2 px  ，联立 2 2 2 px y px     ，可得 y p ， 则 AF p ，且 EF p ， 2 2 2 2EA AF EF p     ，解得 2p  ， 因此，抛物线的标准方程为 2 2 2y x ； （2）设直线 AB 的方程为 2 2x my  ， 由 2 2 2 2 2 y x x my     ，得 2 2 2 2 0y my   ， 设点  1 1,A x y 、  2 2,B x y ，所以 1 2 2 2y y m  ， 1 2 2y y   ， 直线 AE 方程为 1 1 2 22 2 yy x x       ， 令 0x  ，得 1 1 1 1 2 2 2 2 2 2 2 M y y y myx    ，同理 2 2 2 2 2 2 2 2 2 2 2 N y y y myx    ， - 26 - 所以      1 21 2 1 2 1 2 22 2 2 22 2 2 2M N y yy yy y my my my my            1 2 1 22 2 y y my my    其中     2 2 2 2 1 2 1 2 1 22 2 2 2 2 4 2 2 2my my m y y m y y m m m            ， 则 1 2 21 2 1 2 4 4 41 2 M N EF y yS mS EO y y       ，当 0m  时等号成立， 因此 1 2 S S 的取值范围为 4, ． 【点睛】本题考查抛物线方程的求解，同时也考查了抛物线中三角形面积比的取值范围的求 解，考查计算能力，属于中等题. - 27 -