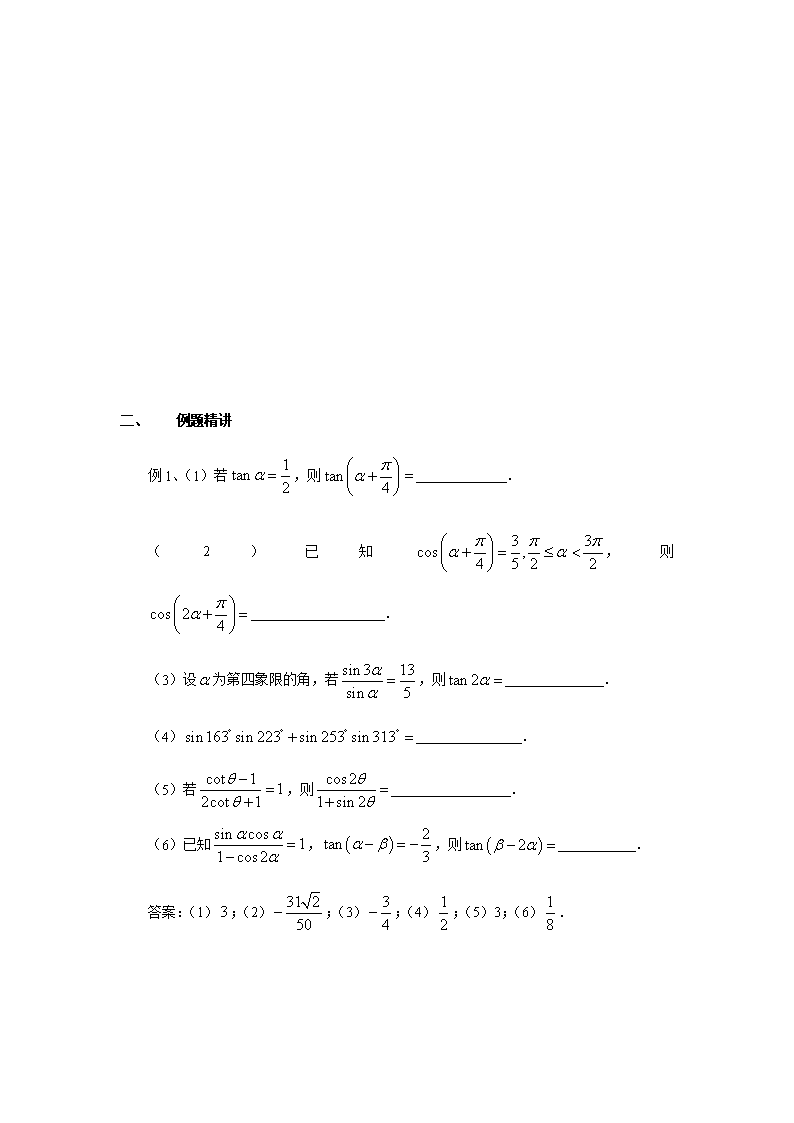2020届二轮复习三角恒等变形1（教师）学案（全国通用） 9页

三角恒等变形1‎ 一、 知识要点 1、 两角和与差的正弦、余弦和正切公式 ‎1）；‎ ‎2）；‎ ‎3）．‎ 2、 二倍角的正弦、余弦和正切公式 ‎1）；‎ ‎2）；‎ ‎3）．‎ 3、 半角的正弦、余弦和正切公式 ‎1）；2）；3）；‎ ‎4）‎ 4、 辅助角公式 ‎（其中角所在象限由符号确定，的值由确定）‎ 一、 例题精讲 例1、（1）若，则 ．‎ ‎（2）已知，则 ．‎ ‎（3）设为第四象限的角，若，则 ．‎ ‎（4） ．‎ ‎（5）若，则 ．‎ ‎（6）已知，，则 ．‎ 答案：（1）；（2）；（3）；（4）；（5）3；（6）．‎ 例2、（1）已知，求的值；‎ ‎（2）已知（其中为锐角），求的值；‎ ‎（3）已知，，且，，求的值．‎ 答案：（1）；（2）4；（3）．‎ 例3、（1）化简：（为锐角）；‎ ‎（2）化简：．‎ 答案：（1）；（2）．‎ 例4、已知，，求的值．‎ 答案：‎ 例5、已知：，，求，，的值．‎ 答案：‎ 例6、已知，，且，求的值．‎ 答案：‎ ‎*例7、已知是关于的方程的两个实数根，且，求的取值范围．‎ 答案：‎ ‎*例8、在中，，求的取值范围．‎ 答案：‎ 一、 课堂练习 ‎1、如果，，那么 ．‎ 答案：‎ ‎2、若，则的取值范围是 ．‎ 答案：或 ‎3、 ．‎ 答案：‎ ‎4、化简 （其中）．‎ 答案：‎ ‎5、函数的最小正周期是 ．‎ 答案：‎ 一、 课后作业 一、填空题 ‎1、已知，则 ．‎ 答案：‎ ‎2、 ．‎ 答案：1‎ ‎3、已知为锐角，，，则 ．‎ 答案：‎ ‎4、已知为锐角，且，，则 ．‎ 答案：‎ ‎5、已知是第二象限的角，，则 ．‎ 答案：‎ ‎6、设，，，，则 ．‎ 答案：‎ 二、选择题 ‎7、设，，则的值是（ ）‎ A、 B、 C、 D、‎ 答案：A ‎8、已知，，为锐角，则的值为（ ）‎ A、 B、 C、或 D、‎ 答案：D ‎9、如果的内角成等差数列，那么的取值范围是（ ）‎ A、 B、 C、 D、‎ 答案：D 三、解答题 ‎10、已知，且，．‎ ‎（1）分别求和的值；‎ ‎（2）求的值．‎ 答案：（1），；（2）‎ ‎11、已知，、是方程的两根，求的值．‎ 答案：‎ ‎12、（1）设，，求的值；‎ ‎（2）已知，，求 的值．‎ 答案：（1）；（2）‎