2020届二轮复习空间向量在立体几何中的应用教案（全国通用） 17页

‎2020届二轮复习 空间向量在立体几何中的应用 教案（全国通用）‎ 类型一、空间向量的运算 ‎【例1】已知=（2，2，1），=（4，5，3），求平面ABC的单位法向量。‎ ‎【答案】单位法向量=±（，－，）.‎ ‎【解析】设面ABC的法向量，则⊥且⊥，即 ‎，即，解得，‎ 令，则 ‎∴单位法向量=±（，－，）.‎ ‎【总结升华】一般情况下求法向量用待定系数法。由于法向量没规定长度，仅规定了方向，所以有一个自由度，可把的某个坐标设为1，再求另两个坐标。平面法向量是垂直于平面的向量，故法向量的相反向量也是法向量，所以本题的单位法向量应有两解。‎ 举一反三：‎ ‎【变式】若＝(1,5,－1)，＝(－2,3,5)‎ ‎（1）若，求实数k的值；‎ ‎（2）若，求实数k的值；‎ ‎（3）若取得最小值，求实数k的值。‎ ‎【答案】‎ ‎(1)‎ ‎，即 由，解得； ‎ ‎(2)，‎ ‎，‎ 即，解得；‎ ‎(3) ‎ 当时，取得最小值。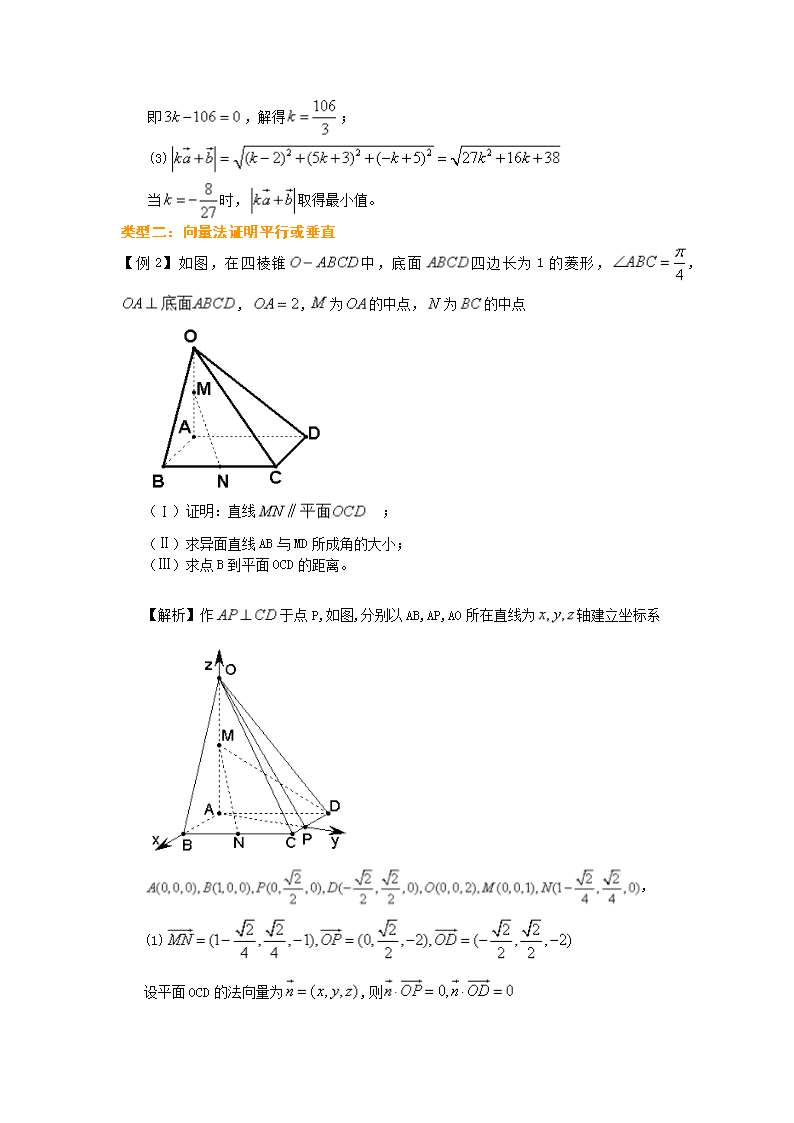‎ 类型二：向量法证明平行或垂直 ‎【例2】如图，在四棱锥中，底面四边长为1的菱形，, , ,为的中点，为的中点 ‎（Ⅰ）证明：直线；‎ ‎（Ⅱ）求异面直线AB与MD所成角的大小； ‎ ‎（Ⅲ）求点B到平面OCD的距离。‎ ‎【解析】作于点P,如图,分别以AB,AP,AO所在直线为轴建立坐标系 ‎,‎ ‎(1)‎ 设平面OCD的法向量为,则 即 ‎ 取,解得 ‎(2)设与所成的角为,‎ ‎ , 与所成角的大小为 ‎(3)设点B到平面OCD的距离为,则为在向量上的投影的绝对值,‎ 由 , 得.‎ 所以点B到平面OCD的距离为 ‎【总结升华】1. 用向量证明线面平行的方法有：‎ ‎(1)证明该直线的方向向量与平面的某一法向量垂直；‎ ‎(2)证明该直线的方向向量与平面内某直线的方向向量平行；‎ ‎(3)证明该直线的方向向量可以用平面内的两个不共线的向量线性表示．‎ ‎2. 用向量法证垂直问题：‎ ‎(1)证明线线垂直，只需证明两直线的方向向量数量积为0；‎ ‎(2)证明线面垂直，只需证明直线的方向向量与平面的法向量共线，或利用线面垂直的判定定理转化为证明线线垂直；‎ ‎(3)证明面面垂直，只需证明两平面的法向量的数量积为0，或利用面面垂直的判定定理转化为证明线面垂直．‎ 举一反三：‎ ‎【变式】ID 401056【高清视频空间向量在立体几何中的应用例题1】‎ 如图，已知直三棱柱ABC－A1B‎1C1中，△ABC为等腰直角三角形，∠BAC＝90°，且AB＝AA1，D、E、F分别为B‎1A、C‎1C、BC的中点．求证：‎ ‎(1)DE∥平面ABC；‎ ‎(2)B‎1F⊥平面AEF.‎ ‎【解析】如图建立空间直角坐标系A－xyz，令AB＝AA1＝4，‎ 则A(0，0，0)，E(0，4，2)，F(2，2，0)，B(4，0，0)，B1(4，0，4)．‎ ‎(1)取AB中点为N，则N(2，0，0)，C(0，4，0)，D(2，0，2)，‎ ‎∴＝(－2，4，0)，＝(－2，4，0)，‎ ‎∴＝.∴DE∥NC，‎ 又NC在平面ABC内，DE不在平面ABC内，故DE∥平面ABC.‎ ‎(2)＝(－2，2，－4)，＝(2，－2，－2)，‎ ＝(2，2，0)，‎ ·＝(－2)×2＋2×(－2)＋(－4)×(－2)＝0，‎ 则⊥，∴B‎1F⊥EF，‎ ‎∵·＝(－2)×2＋2×2＋(－4)×0＝0.‎ ‎∴⊥，即B‎1F⊥AF，‎ 又∵AF∩FE＝F，∴B‎1F⊥平面AEF.‎ 类型三：异面直线所成的角 ‎【例3】正方体ABCD-EFGH的棱长为a，点P在AC上，Q在BG上，且AP=BQ=a, 求直线PQ与AD所成的角 ‎【答案】90°‎ ‎【解析】建立空间直角坐标系如图，则，‎ ‎,‎ ‎∴,，‎ ‎∴‎ ‎∴QP与AD所成的角为90°。‎ ‎【总结升华】建立坐标系后，求出 可由求解。‎ 举一反三：‎ ‎【变式】如图，在直四棱柱中，底面是边长为的菱形，侧棱长为 ‎（1）与能否垂直？请证明你的判断；‎ ‎（2）当在上变化时，求异面直线与所成角的取值范围。‎ ‎【答案】∵菱形中，于，设，‎ 分别以所在直线为轴，建立空间直角坐标系，‎ 设，则 ‎（1）∵，‎ ‎∴，∴与不能垂直。‎ ‎（2）∵，∴，∵‎ ‎∴，‎ ‎，‎ ‎∵，∴设，‎ 又，∴‎ ‎∵，∴‎ ‎∴直线与所成角的取值范围是。‎ 类型四：直线与平面所成的角 ‎【例4】如图，在棱长为1的正方体中，是侧棱上的一点，。试确定，使直线与平面所成角的正切值为；‎ ‎【解析】建立如图所示的空间直角坐标系，‎ 则A(1,0,0),B(1,1,0),P(0,1,ｍ)，C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1).‎ 所以 又由的一个法向量.‎ 设与所成的角为，‎ 则 依题意有，解得.‎ 故当时，直线。‎ 举一反三：‎ ‎【变式】如图，三棱锥P-ABC中，∠ABC=，PA=1，AB=，AC=2，PA⊥面ABC．‎ ‎(1)求直线AB和直线PC所成角的余弦值；‎ ‎(2)求PC和面ABC所成角的正弦值；‎ ‎【答案】 ‎ ‎(1)以A为坐标原点，分别以AB、AP所在直线为y轴、z轴,以过A点且平行于BC直线为x轴建立空间直角坐标系.‎ 在直角△ABC中,∵AB=，AC=2，∴BC=1‎ A(0,0,0)，B(0,,0)，C(1,,0)，P(0,0,1).‎ ‎(0,,0)，(1,,),‎ cos<,>===‎ ‎∴直线AB与直线PC所成的角余弦为.‎ ‎(2)取平面ABC的一个法向量=(0，0，1)，‎ 设PC和面ABC所成的角为，则 sin=|cos<，>|==.‎ ‎∴PC和面ABC所成的角的正弦值为．‎ 类型五：二面角 ‎【例5】 ID 401056 【高清视频空间向量在立体几何中的应用例题2】如图，在三棱柱ABC－A1B‎1C1中，H是正方形AA1B1B的中心，AA1＝2，C1H⊥平面AA1B1B，且C1H＝.‎ ‎(1)求异面直线AC与A1B1所成角的余弦值；‎ ‎(2)求二面角A－A‎1C1－B1的正弦值；‎ ‎(3)设N为棱B‎1C1的中点，点M在平面AA1B1B内，且MN⊥平面A1B‎1C1，求线段BM的长．‎ ‎【解析】如图所示，建立空间直角坐标系，点B为坐标原点，依题意得A(2，0，0)，B(0，0，0)，C(，－，)，A1(2，2，0)，B1(0，2，0)，C1(，，)．‎ ‎(1)易得＝(－，－，)，＝(－2，0，0)，‎ 于是cos〈，〉＝＝＝，‎ 所以异面直线AC与A1B1所成角的余弦值为.‎ ‎(2)易知＝(0，2，0)，＝(－，－，)．‎ 设平面AA‎1C1的一个法向量m＝(x，y，z)，则 即不妨令x＝，可得m＝(，0，)．‎ 设平面A1B‎1C1的一个法向量n＝(x，y，z)，则 即不妨令y＝，可得n＝(0，，)．‎ 则cos〈m，n〉＝＝＝，从而sin〈m，n〉＝，‎ 所以二面角A－A‎1C1－B1的正弦值为.‎ ‎(3)由N为棱B‎1C1的中点，得N(，，)．设M(a，b，0)，‎ 则＝(－a，－b，)．因为MN⊥平面A1B‎1C1，‎ 由(2)知平面A1B‎1C1的一个法向量为n＝(0，，)，所以∥n，‎ 所以－a＝0，＝，‎ 解得.故M(，，0)．因此＝(，，0)，所以线段BM的长||＝.‎ ‎【总结升华】求两异面直线所成的角，用向量法就是求两直线上的两方向向量的夹角，但需注意二者范围的区别．同样地，利用向量法求二面角的大小，就是求两个半平面的法向量的夹角(或夹角的补角)，在具体求解中应适当选取或求解直线的方向向量及平面的法向量．在空间直角坐标系中，常采用待定系数法求平面的法向量．‎ 举一反三：‎ ‎【变式】如图，矩形ABCD和梯形BEFC所在平面互相垂直，BE∥CF，∠BCF=∠CEF=90°，，EF=2。‎ ‎（Ⅰ）求证：AE∥平面DCF；‎ ‎（Ⅱ）当AB的长为何值时，二面角A—EF—C的大小为60°？‎ ‎【解析】如图，以点为坐标原点，以和分别作为轴，轴和轴，建立空间直角坐标系．‎ D A B E F C y z x 设，‎ 则，，，，．‎ ‎（Ⅰ）证明：，，，‎ 所以，，从而，，‎ 所以平面．‎ 因为平面，所以平面平面．‎ 故平面．‎ ‎（Ⅱ）解：因为，，‎ 所以，，从而 解得．所以，．‎ 设与平面垂直，‎ 则，，解得．‎ 又因为平面，，‎ 所以，得到．‎ 所以当为时，二面角的大小为．‎ 类型六：空间距离 ‎【例5】如图，△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，AB＝2.求点A到平面MBC的距离．‎ ‎【解析】‎ 取CD中点O，连接OB，OM，‎ 则OB⊥CD，OM⊥CD.‎ 又平面MCD⊥平面BCD，‎ 所以MO⊥平面BCD.‎ 取O为原点，直线OC、BO、OM为x轴、y轴、z轴，建立空间直角坐标系如图．OB＝OM＝，则各点坐标分别为C(1，0，0)，M(0，0，)，B(0，－，0)，A(0，－，2)．‎ ‎(1)设是平面MBC的法向量，则 ＝(1，，0)，＝(0，，)．‎ 由⊥得·＝0即x＋y＝0；‎ 由⊥得·＝0即y＋z＝0.‎ 取＝(，－1，1)，＝(0，0，2)，‎ 则d＝＝＝.‎ 故点A到平面MBC的距离为.‎ 法二：(1)取CD中点O，连OB，OM，‎ 则OB＝OM＝，OB⊥CD，MO⊥CD，‎ 又平面MCD⊥平面BCD，‎ 则MO⊥平面BCD，‎ 所以MO∥AB，所以MO∥平面ABC，‎ 故M，O到平面ABC的距离相等．‎ 作OH⊥BC于H，连MH，则MH⊥BC.‎ 求得OH＝OC·sin60°＝，‎ MH＝ ‎＝.‎ 设点A到平面MBC的距离为d，‎ 由VA－MBC＝VM－ABC得 ·S△MBC·d＝·S△ABC·OH.‎ 即××2×d＝××2×2×，‎ 解得d＝.‎ ‎【总结升华】利用向量法求点到平面的距离的步骤如下：(1)求出该平面的一个法向量；(2)找出以该点及平面内的某点为端点的线段对应的向量；(3)利用公式d＝求距离．‎ 举一反三：‎ ‎【变式】如图，四面体ABCD中，O、E分别是BD、BC的中点，，,求点E到平面ACD的距离。‎ ‎【答案】以O为原点，如图建立空间直角坐标系，‎ 则 设平面ACD的法向量为则 ‎，令得是平面ACD的一个法向量。‎ 又 点E到平面ACD的距离 类型七、利用空间向量解决立体几何中的探索问题 ‎【例6】在四棱锥中，//，，，平面，. （Ⅰ）设平面平面，求证：//； （Ⅱ）求证：平面；（Ⅲ）设点为线段上一点，且直线 与平面所成角的正弦值为，求的值．‎ ‎【证明】（Ⅰ） 因为//，平面，平面，‎ 所以//平面. ‎ 因为平面，平面平面，‎ 所以//. ‎ ‎（Ⅱ）：因为平面，，所以以为坐标原点，所在的直线分别为轴、轴、轴建立空间直角坐标系，‎ 则，，，. ‎ 所以 ，，‎ ‎，‎ 所以，‎ ‎.‎ 所以 ，. ‎ 因为 ，平面，‎ 平面，‎ 所以 平面. ‎ ‎（Ⅲ）解：设（其中），，直线与平面所成角为.‎ 所以 .‎ 所以 .‎ 所以 即. ‎ 所以 . ‎ 由（Ⅱ）知平面的一个法向量为. ‎ 因为 ，‎ 所以 .‎ 解得 .‎ 所以 . ‎ ‎【总结升华】空间向量最适合于解决这类立体几何中的探索性问题，它无需进行复杂繁难的作图、论证、推理，只需通过坐标运算进行判断。在解题过程上中，往往把“是否存在”问题，转化为“点的坐标是否有解，是否有规定范围的解”等，所以使问题的解决更简单、有效，在立体几何二轮复习中，我们要善于运用这一方法。‎ 举一反三：‎ ‎【变式】‎ 在如图所示的几何体中，四边形为平行四边形，， 平面，，，，，且是的中点.（Ⅰ）求证：平面；（Ⅱ）求二面角的大小；（Ⅲ）在线段上是否存在一点，使得与所成的角为？若存在，求出的长度；若不存在，请说明理由.‎ C A F E B M D ‎【解析】（Ⅰ）取的中点，连接.‎ N C A F E B M D 在△中，是的中点，是的中点，所以，‎ ‎ 又因为，‎ ‎ 所以且.‎ 所以四边形为平行四边形，‎ 所以.‎ 又因为平面，平面，‎ ‎ 故平面. ‎ 解法二：因为平面，，故以为原点，建立如图所示的空间直角坐标系. ……1分 ‎ 由已知可得 ‎ z C A F E B M D x y ‎（Ⅰ）， . ‎ 设平面的一个法向量是.‎ ‎ 由得 ‎ 令，则. ‎ 又因为，‎ ‎ 所以，又平面，所以平面. ‎ ‎（Ⅱ）由（Ⅰ）可知平面的一个法向量是.‎ ‎ 因为平面，所以.‎ ‎ 又因为，所以平面.‎ ‎ 故是平面的一个法向量.‎ ‎ 所以，又二面角为锐角，‎ ‎ 故二面角的大小为. ‎ ‎ （Ⅲ）假设在线段上存在一点，使得与所成的角为.‎ ‎ 不妨设（），则.‎ ‎ 所以，‎ ‎ 由题意得，‎ ‎ 化简得， ‎ ‎ 解得. ‎ ‎ 所以在线段上不存在点，使得与所成的角为. ‎