【数学】2020届一轮复习人教B版（理）第八章35空间几何体的结构及三视图、直观图作业 9页

‎【课时训练】第35节　空间几何体的结构 及三视图、直观图 一、选择题 ‎1．(2018张家界模拟)沿一个正方体三个面的对角线截得的几何体如图所示，则该几何体的侧视图为(　　)‎ A　　　　B　　　　　C　　　 　D ‎【答案】B ‎【解析】结合几何体及选项知B正确．‎ ‎2．(2018甘肃一模)如图所示，等腰△A′B′C′是△ABC的直观图，那么△ABC是(　　)‎ A．等腰三角形 ‎ B．直角三角形 C．等腰直角三角形 ‎ D．钝角三角形 ‎【答案】B ‎【解析】由题图知A′C′∥y′轴，A′B′∥x′轴，由斜二测画法知在△ABC中，AC∥y轴，AB∥x轴，∴AC⊥AB.又因为A′C′＝A′B′，∴AC＝2AB≠AB.‎ ‎∴△ABC是直角三角形．‎ ‎3．(2018广东佛山一模)底面水平放置的正三棱柱的所有棱长均为2，当其正视图有最大面积时，其侧视图的面积为(　　)‎ A．2 B．3‎ C． D．4‎ ‎【答案】A ‎【解析】当正视图的面积最大时，可以按如图所示放置，可知其侧面的面积S侧＝2　.‎ ‎4．(2018太原模拟)一个正三棱柱的正(主)视图和俯视图如图所示，则这个三棱柱的侧(左)视图的面积为(　　)‎ A．6　　 B．8‎ C．8 D．12‎ ‎【答案】A ‎【解析】该三棱柱的侧(左)视图为一个矩形，由“长对正，高平齐，宽相等”的原理知，其侧(左)视图的底边长为俯视图中正三角形的高，即为2，侧(左)视图的高为3，故其侧(左)视图的面积为S＝2×3＝6.故选A.‎ ‎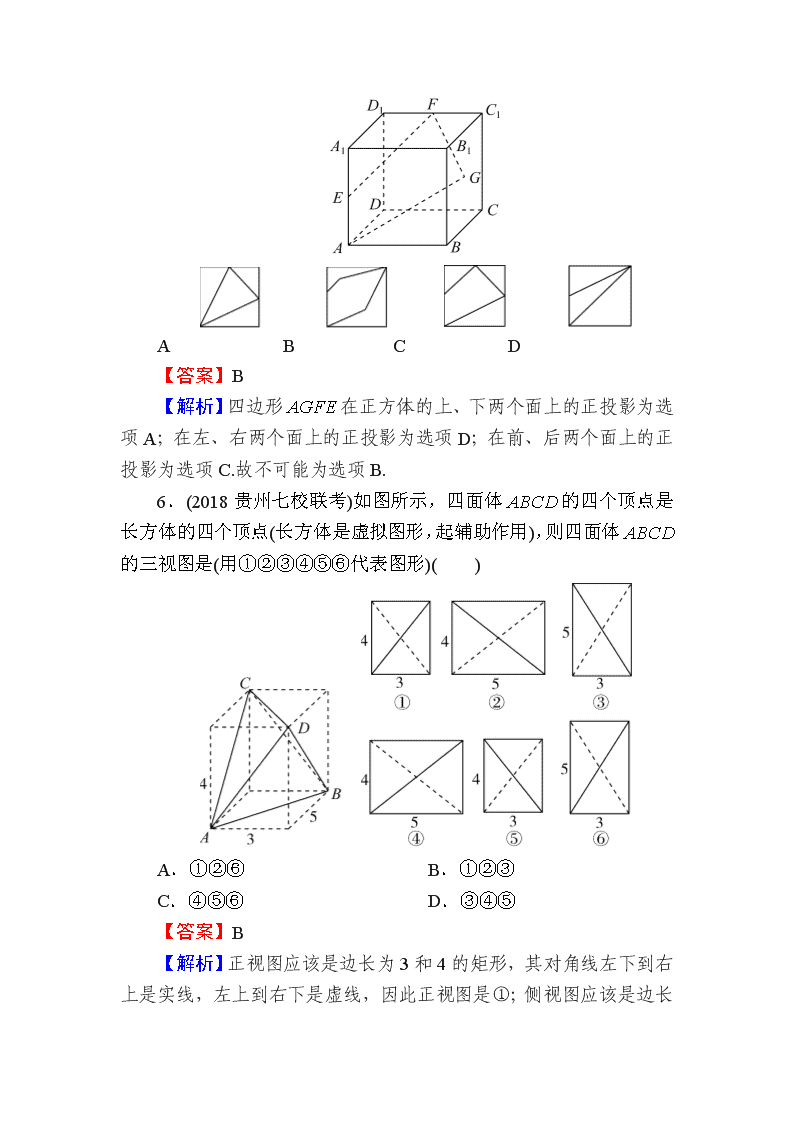5．(2018四川省级联考)如图，在正方体ABCD－A1B‎1C1D1中，E，F分别是AA1、C1D1的中点，G是正方形BCC1B1的中心，则空间四边形AGFE在该正方体的表面上的正投影不可能是(　　)‎ ‎　　　‎ A　　　　　　B　　　　 　C　 　 　　　D ‎【答案】B ‎【解析】四边形AGFE在正方体的上、下两个面上的正投影为选项A；在左、右两个面上的正投影为选项D；在前、后两个面上的正投影为选项C.故不可能为选项B.‎ ‎6．(2018贵州七校联考)如图所示，四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)(　　)‎ ‎　‎ A．①②⑥　　 B．①②③‎ C．④⑤⑥ D．③④⑤‎ ‎【答案】B ‎【解析】正视图应该是边长为3和4的矩形，其对角线左下到右上是实线，左上到右下是虚线，因此正视图是①‎ ‎；侧视图应该是边长为5和4的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此侧视图是②；俯视图应该是边长为3和5的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此俯视图是③.故选B.‎ ‎7．(2018安徽马鞍山一模)用斜二测画法画出的某平面图形的直观图如图，边AB平行于y轴，BC，AD平行于x轴．已知四边形ABCD的面积为‎2　 cm2，则原平面图形的面积为(　　)‎ A．‎4 cm2　　 B．‎4　 cm2‎ C．‎8 cm2 D．‎8　 cm2‎ ‎【答案】C ‎【解析】由题意可知∠BAD＝45°，则原平面图形为直角梯形，上、下底面的长与BC，AD相等，高为梯形ABCD的高的2倍，所以原平面图形的面积为‎8 cm2.‎ ‎8．(2018邯郸模拟)已知一个三棱锥的三视图如图所示，其中三个视图都是直角三角形，则在该三棱锥的四个面中，直角三角形的个数为(　　)‎ A．1 B．2‎ C．3 D．4‎ ‎【答案】D ‎【解析】由题意可知，该几何体是三棱锥，‎ 其放置在长方体中形状如图所示(图中棱锥P－ABC)，利用长方体模型可知，此三棱锥的四个面全部是直角三角形．故选D.‎ ‎9．(2018永州模拟)如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的各个面中最大面的面积为(　　)‎ A．1 B． C． D．2 ‎【答案】D ‎【解析】由题意知，该几何体的直观图为三棱锥A－BCD，如图，其最大面的表面是边长为2　的等边三角形，故其面积为×2　×＝2　.‎ ‎10．(2018南阳联考)已知一个三棱锥的俯视图与侧(左)视图如图所示，俯视图是边长为2的正三角形，‎ 侧(左)视图是有一条直角边为2的直角三角形，则该三棱锥的正(主)视图可能为(　　)‎ A　　　　　　B　　　　　C　　　　　　D ‎【答案】C ‎【解析】由已知条件得直观图如图所示，则正(主)视图是直角三角形，中间的线是看不见的线PA形成的投影，应为虚线．故选C.‎ ‎11．(2018临沂模拟)如图1，将一个正三棱柱ABC－DEF截去一个三棱锥A－BCD，得到几何体BCDEF，如图2，则该几何体的正(主)视图是(　　)‎ A　　　　　B　　　 　　C　　　　　D ‎【答案】C ‎【解析】由于三棱柱为正三棱柱，故平面ADEB⊥平面DEF，△‎ DEF是等边三角形，所以CD在后侧面上的投影为AB的中点与D的连线，CD的投影与底面不垂直．故选C.‎ ‎12．(2018南昌模拟)如图，在正四棱柱ABCD－A1B‎1C1D1中，点P是平面A1B‎1C1D1内一点，则三棱锥P－BCD的正(主)视图与侧(左)视图的面积之比为(　　)‎ A．1∶1 B．2∶1‎ C．2∶3 D．3∶2‎ ‎【答案】A ‎【解析】根据题意，三棱锥P－BCD的正视图是三角形，且底边为正四棱柱的底面边长，高为正四棱柱的高；侧视图是三角形，且底边为正四棱柱的底面边长，高为正四棱柱的高．故三棱锥P－BCD的正(主)视图与侧(左)视图的面积之比为1∶1.‎ 二、填空题 ‎13．(2019河南濮阳质检)给出下列命题：①在正方体上任意选择4个不共面的顶点，它们可能是正四面体的4个顶点；②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；③若有两个侧面垂直于底面，则该四棱柱为直四棱柱．其中正确命题的序号是________．‎ ‎【答案】①‎ ‎【解析】①正确，正四面体是每个面都是等边三角形的四面体，如正方体ABCD－A1B‎1C1D1中的四面体A－CB1D1；②错误，反例如图所示，底面△ABC为等边三角形，可令AB＝VB＝VC＝BC＝AC，则△VBC为等边三角形，△VAB和△VCA均为等腰三角形，‎ 但不能判定其为正三棱锥；③错误，必须是相邻的两个侧面．‎ ‎14．(2018湖北襄阳模拟)如图所示，△A′B′C′是△ABC的直观图，且△A′B′C′是边长为a的正三角形，则△ABC的面积为________．‎ ‎【答案】a2‎ ‎【解析】如图所示，△A′B′C′是边长为a的正三角形，‎ 作C′D′∥A′B′交y′轴于点D′，则C′，D′到x′轴的距离为a.‎ ‎∵∠D′A′B′＝45°，∴A′D′＝a，‎ 由斜二测画法的法则，知 在△ABC中，AB＝A′B′＝a，AB边上的高是A′D′的二倍，即为a，‎ ‎∴S△ABC＝a·a＝a2.‎ 三、解答题 ‎15．(2018湖南衡阳八中月考)已知正三棱锥V－ABC的正视图、侧视图和俯视图如图所示．‎ ‎(1)画出该三棱锥的直观图；‎ ‎(2)求出侧视图的面积．‎ ‎【解】(1)直观图如图所示．‎ ‎(2)根据三视图间的关系可得BC＝2　，‎ ‎∴侧视图中VA＝＝2，∴S△VBC＝×2　×2　＝6.‎