2020届二轮复习统计与概率学案（全国通用） 20页

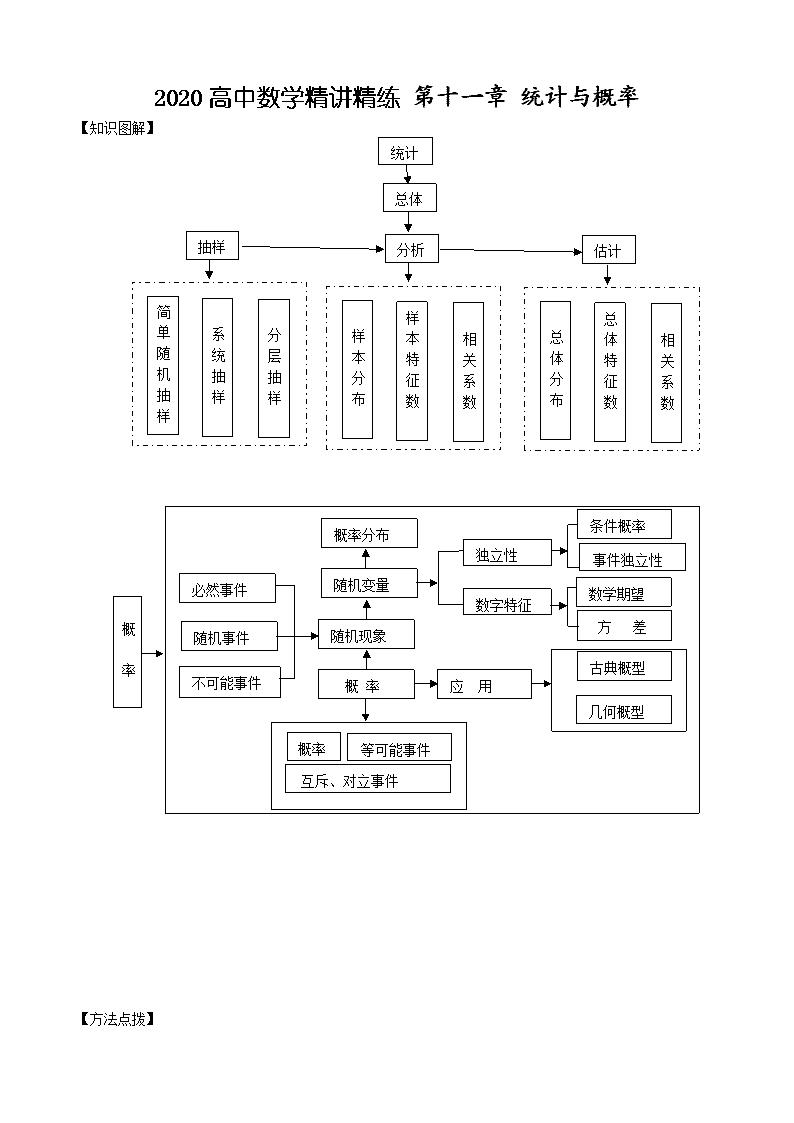
‎2020高中数学精讲精练 第十一章 统计与概率 总体 抽样 分析 估计 简单随机抽样 系统抽样 分层抽样 样本分布 样本特征数 相关系数 总体分布 总体特征数 相关系数 统计 ‎【知识图解】‎ 概 率 等可能事件 必然事件 随机事件 不可能事件 概率分布 随机变量 随机现象 概 率 独立性 数字特征 条件概率 事件独立性 数学期望 方 差 应 用 古典概型 几何概型 概率 互斥、对立事件 ‎【方法点拨】‎ 1、 准确理解公式和区分各种不同的概念 正确使用概率的加法公式与乘法公式、随机变量的数学期望与方差的计算公式.注意事件的独立性与互斥性是两个不同的概念，古典概型与几何概型都是等可能事件，对立事件一定是互斥事件，反之却未必成立.‎ 2、 掌握抽象的方法 抽象分为简单的随机抽样、系统抽样、分层抽样.系统抽样适用于总体较多情况，分层抽样适用于总体由几个差异明显的部分组成的情况.‎ 3、 学会利用样本和样本的特征数去估计总体 会列频率分布表，会画频率分布直方图、频率折线图、茎叶图，并体会它们各自特点，特别注意频率分布直方图的纵坐标为频率/组距；会计算样本数据平均数、方差（标准差），利用样本的平均数可以估计总体的平均数，利用样本的方差估计总体的稳定程度.‎ 4、 关于线性回归方程的学习 在线性相关程度进行校验的基础上，建立线性回归分析的基本算法步骤.学会利用线性回归的方法和最小二乘法研究回归现象，得到的线性回归方程（不要求记忆系数公式）可用于预测和估计，为决策提供依据.‎ 第1课 抽样方法 ‎【考点导读】‎ ‎1. 抽样方法分为简单随机抽样、系统抽样、分层抽样.‎ ‎2 .系统抽样适用于总体个数较多情况，分层抽样适用于总体由几个差异明显的部分组成的情况.‎ ‎【基础练习】‎ ‎1．为了了解全校900名高一学生的身高情况，从中抽取90名学生进行测量，下列说法正确的是 ④ . ‎ ‎①总体是900 ②个体是每个学生 ③样本是90名学生 ④样本容量是90‎ ‎2．对总数为N的一批零件抽取一个容量为30的样本，若每个零件被抽到的概率为0.25，则N的值为 120 .‎ ‎3．高三年级有12个班，每班50人按1—50排学号，为了交流学习经验，要求每班学号为18的同学留下进行交流，这里运用的是 系统 抽样法.‎ ‎4．某校有学生2000人，其中高三学生500人．为了解学生身体情况，采用按年级分层抽样的方法，从该校学生中抽取一个200人的样本，则样本中高三学生的人数为 50 ‎ ‎5.将参加数学竞赛的1000名学生编号如下：0001，0002，0003，…，1000，打算从中抽取一个容量为50的样本，按系统抽样的方法分成50个部分，如果第一部分编号为0001，0002，0003，…，0020，第一部分随机抽取一个号码为0015，则抽取的第40个号码为 0795 ．‎ ‎【范例解析】‎ 例1：某车间工人加工一种轴100件，为了了解这种轴的直径，要从中抽取10件轴在同一条件下测量，如何采用简单随机抽样的方法抽取样本？‎ 分析 简单随机抽样一般采用两种方法：抽签法和随机数表法.‎ 解法1：（抽签法）将100件轴编号为1，2，…‎ ‎，100，并做好大小、形状相同的号签，分别写上这100个数，将这些号签放在一起，进行均匀搅拌，接着连续抽取10个号签，然后测量这个10个号签对应的轴的直径.‎ 解法2：（随机数表法）将100件轴编号为00，01，…99，在随机数表中选定一个起始位置，如取第21行第1个数开始，选取10个为68，34，30，13，70，55，74，77，40，44，这10件即为所要抽取的样本.‎ 点评 从以上两种方法可以看出，当总体个数较少时用两种方法都可以，当样本总数较多时，方法2优于方法1.‎ 例2、某校高中三年级的295名学生已经编号为1，2，……，295，为了了解学生的学习情况，要按1：5的比例抽取一个样本，用系统抽样的方法进行抽取，并写出过程.‎ 分析 按1：5分段，每段5人，共分59段，每段抽取一人，关键是确定第1段的编号.‎ 解：按照1：5的比例，应该抽取的样本容量为295÷5=59，我们把259名同学分成59组，每组5人，第一组是编号为1～5的5名学生，第2组是编号为6～10的5名学生，依次下去，59组是编号为291～295的5名学生.采用简单随机抽样的方法，从第一组5名学生中抽出一名学生，不妨设编号为k(1≤k≤5)，那么抽取的学生编号为k+5L(L=0,1,2,……，58)，得到59个个体作为样本，如当k=3时的样本编号为3，8，13，……，288，293.‎ 点评 系统抽样可按事先规定的规则抽取样本. 本题采用的规则是第一组随机抽取的学生编号为k，那么第m组抽取的学生编号为k+5(m-1).‎ 例3：一个地区共有5个乡镇，人口3万人，其中人口比例为3：2：5：2：3，从3万人中抽取一个300人的样本，分析某种疾病的发病率，已知这种疾病与不同的地理位置及水土有关，问应采取什么样的方法？并写出具体过程.‎ 分析 采用分层抽样的方法.‎ 解：因为疾病与地理位置和水土均有关系，所以不同乡镇的发病情况差异明显，因而采用分层抽样的方法，具体过程如下：‎ ‎（1）将3万人分为5层，其中一个乡镇为一层.‎ ‎（2）按照样本容量的比例随机抽取各乡镇应抽取的样本.‎ ‎300×3/15=60（人），300×2/15=40（人），300×5/15=100（人），300×2/15=40（人），300×3/15=60（人），因此各乡镇抽取人数分别为60人、40人、100人、40人、60 人.‎ ‎（3）将300人组到一起，即得到一个样本.‎ 点评 分层抽样在日常生活中应用广泛，其抽取样本的步骤尤为重要，应牢记按照相应的比例去抽取.‎ ‎【反馈演练】‎ ‎1. 一个总体中共有200个个体，用简单随机抽样的方法从中抽取一个容量为20的样本，则某一特定个体被抽到的可能性是 0.1 .‎ ‎2．为了了解参加运动会的2000名运动员的年龄情况，从中抽取100名运动员；就这个问题，下列说法中正确的有 2 个.‎ ‎①2000名运动员是总体；②每个运动员是个体；③所抽取的100名运动员是一个样本；‎ ‎④样本容量为100；⑤这个抽样方法可采用按年龄进行分层抽样；⑥每个运动员被抽到的概率相等.‎ ‎3．对于简单随机抽样，下列说法中正确的命题为 ①②③④ .‎ ‎①它要求被抽取样本的总体的个数有限，以便对其中各个个体被抽取的概率进行分析；②它是从总体中逐个地进行抽取，以便在抽取实践中进行操作；③它是一种不放回抽样；④它是一种等概率抽样，不仅每次从总体中抽取一个个体时，各个个体被抽取的概率相等，而且在整个抽样过程中，各个个体被抽取的概率也相等，从而保证了这种方法抽样的公平性.‎ ‎4．某公司甲、乙、丙、丁四个地区分别有150 个、120个、180个、150个销售点．公司为了调查销售的情况，需从这600个销售点中抽取一个容量为100的样本，记这项调查为①；在丙地区中有20个特大型销售点，要从中抽取7个调查其收入和售后服务等情况，记这项调查为②．则完成①、②这两项调查宜采用的抽样方法依次是 分层抽样法，简单随机抽样法 . ‎ ‎5.下列抽样中不是系统抽样的是 ③ .‎ ‎①.从标有1～15号的15个球中，任选三个作样本，按从小号到大号排序，随机选起点，以后，（超过15则从1再数起）号入样；‎ ‎②.工厂生产的产品，用传送带将产品送入包装车间前，检验人员从传送带上每隔五分钟抽一件产品进行检验；‎ ‎③.搞某一市场调查，规定在商场门口随机抽一个人进行询问调查，直到调查到事先规定的人数为止；‎ ‎④.电影院调查观众的某一指标，通知每排（每排人数相同）座位号为14的观众留下座谈．‎ ‎6．为了解初一学生的身体发育情况，打算在初一年级10个班的某两个班按男女生比例抽取样本，正确的 抽样方法是 ③ . ‎ ‎①随机抽样 ②分层抽样 ③先用抽签法，再用分层抽样 ④先用分层抽样，再用随机数表法 ‎7．写出下列各题的抽样过程 ‎(1)请从拥有500个分数的总体中用简单随机抽样方法抽取一个容量为30的样本.‎ ‎(2)某车间有189名职工，现在要按1：21的比例选派质量检查员，采用系统抽样的方式进行.‎ ‎(3)一个电视台在因特网上就观众对某一节目喜爱的程度进行调查，参加调查的总人数为12000人，其中持各种态度的人数如下： 　 ‎ 很喜爱 喜爱 一般 不喜爱 ‎2435‎ ‎4567‎ ‎3926‎ ‎1072‎ 打算从中抽取60人进行详细调查，如何抽取？‎ 解：(1)①将总体的500个分数从001开始编号，一直到500号；‎ ‎②从随机数表第1页第0行第2至第4列的758号开始使用该表；‎ ‎③抄录入样号码如下：335、044、386、446、027、420、045、094、382、5215、342、148、407、349、322、027、002、323、141、052、177、001、456、491、261、036、240、115、143、402‎ ‎④按以上编号从总体至将相应的分数提取出来组成样本，抽样完毕 ‎(2)采取系统抽样 189÷21＝9，所以将189人分成9组，每组21人，在每一组中随机抽取1人，这9人组成样本 ‎(3)采取分层抽样 总人数为12000人，12000÷60＝200，‎ 所以从很喜爱的人中剔除145人，再抽取11人；从喜爱的人中剔除167人，再抽取22人；从一般喜爱 的人中剔除126人，再抽取19人；从不喜爱的人中剔除72人，再抽取5人 第2课 总体分布的估计 ‎【考点导读】‎ ‎1．掌握频率分布直方图、折线图表与茎叶图的做法，体会它们各自的特点.‎ ‎2．会用频率分布直方图、折线图表与茎叶图对总体分布规律进行估计.‎ ‎【基础练习】‎ ‎1．一个容量为n的样本，分成若干组，已知某组的频数和频率分别为60，0.25，则n的值是 　　240　　　‎ ‎2．用样本频率分布估计总体频率分布的过程中，下列说法正确的是 ③ ‎ ‎①总体容量越大，估计越精确 ②总体容量越小，估计越精确 ‎③样本容量越大，估计越精确 ④样本容量越小，估计越精确 ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎78‎ ‎02223666778‎ ‎0012234466788‎ ‎0234‎ ‎3． 已知某工厂工人加工的零件个数的茎叶图如右图所示 ‎（以零件个数的前两位为茎，后一位为叶），那么工人生产 零件的平均个数及生产的零件个数超过130的比例分别是 ‎120.5与10％ . ‎ ‎ ‎ ‎4．容量为100的样本数据，按从小到大的顺序分为8组，如下表：‎ 组号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 频数 ‎10‎ ‎13‎ x ‎14‎ ‎15‎ ‎13‎ ‎12‎ ‎9‎ 频率 ‎0.4‎ ‎0.2‎ ‎0.1‎ ‎0‎ ‎40 50 60 70 80 时速 第三组的频数和频率分别是 14和0.14 .‎ ‎5． 200辆汽车通过某一段公路时的时速频率 分布直方图如图所示，则时速在的汽 车大约有 60 辆.‎ ‎【范例解析】‎ 例1．如图，从参加环保知识竞赛的学生中抽出名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：‎ ‎（1）这一组的频数、频率分别是多少？‎ ‎（2）估计这次环保知识竞赛的及格率（分及以上为及格）.‎ 解：（1）频率为：，频数：‎ ‎（2）. ‎ 例2．在参加世界杯足球赛的32支球队中，随机抽取20名队员，调查其年龄为25，21，23，25，27，29，25，28，30，29，26，24，25，27，26，22，24，25，26，28.填写下面的频率分布表，据此估计全体队员在哪个年龄段的人数最多？占总数的百分之几？并画出频率分布直方图．‎ 解： (1)‎ 分组 频数 频率 ‎［20.5,22.5)‎ ‎2‎ ‎0.1‎ ‎［22.5,24.5)‎ ‎3‎ ‎0.15‎ ‎［24.5,26.5)‎ ‎8‎ ‎0.4‎ ‎［26.5,28.5)‎ ‎4‎ ‎0.2‎ ‎［28.5,30.5］‎ ‎3‎ ‎0.15‎ 合计 ‎20‎ ‎1‎ 年龄 频率 组距 ‎20.5 22.5 24.5 26.5 28.5 30.5‎ ‎0.05‎ ‎0.075‎ ‎0.1‎ ‎0.2‎ ‎(2)‎ 分组 频数 频率 ‎［20.5,22.5)‎ ‎［22.5,24.5‎ ‎［24.5,26.5)‎ ‎［26.5,28.5)‎ ‎［28.5,30.5］‎ 合计 ‎（3）估计全体队员在24.5～26.5处人数最多，占总数的百分之四十.‎ ‎【反馈演练】‎ ‎1．对于样本频率直方图与总体密度曲线的关系，下列说法正确的是 ④ ‎ ‎①频率分布直方图与总体密度曲线无关 　　　　 ②频率分布直方图就是总体密度曲线 ‎③样本容量很大的频率分布直方图就是总体密度曲线 ‎ ‎④如果样本容量无限增大,分组的组距无限的减小,那么频率分布直方图就会无限接近于总体密度曲线 ‎ ‎2．在某餐厅内抽取100人,其中有30人在15岁以下,35人在16至25岁,25人在26至45岁,10人在46岁 以上,则数 0．35 是16到25岁人员占总体分布的 ② ‎ ‎ ① 概率 ②频率 ③ 累计频率 ④ 频数 ‎3．10名工人某天生产同一零件，生产的件数是 15 ,17 , 14 , 10 , 15 , 17 ,17 , 16, 14 , 12．‎ 设其平均数为a,中位数为b,众数为c，则a, b, c的大小关系为 ‎ ‎4.已知样本：10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,12则频率为0.3的范围是 ( 2 ) ‎ ‎ ‎ ‎5.已知10个数据如下：63，65，67，69，66，64，66, 64, 65，68.根据这些数据制作频率直方图，其 中[64.5, 66.5)这组所对应矩形的高为 0.2 ‎ ‎6．某中学高一年级有400人，高二年级有320人，高三有280人，以每人被抽取的频率为0.2，向该 中学抽取一个样本容量为n的样本，则n=　　200 　‎ ‎7. 一个容量为20的样本数据,分组后,组距与频数如下: ,2; , 3 ; , 4 ; , 5 ; , 4 ; , 2 .则样本在区间 上的频率为__ 0.7 ___‎ ‎0.5‎ 人数(人)‎ 时间(小时)‎ ‎20‎ ‎10‎ ‎5‎ ‎0‎ ‎1.0‎ ‎1.5‎ ‎2.0‎ ‎15‎ ‎(第9题)‎ ‎8．观察新生婴儿的体重，其频率分布直方图如图所示，则新生婴儿体重在的频率为　　0.3 　　 ‎ ‎(第8题)‎ ‎2400 2700 3000 3300 3600 3900 体重 ‎0‎ ‎0 001‎ 频率/组距 ‎9．某校为了了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，结果用右上面的条形图表示． 根据条形图可得这50名学生这一天平均每人的课外阅读时间为 0.9小时 ‎ ‎10.从甲、乙两台机器生产的零件中随机抽取15个进行检验，相关指标的检验结果为：‎ 甲：534，517，528，522，513，516，527，526，520，508，533，524，518，522，512；‎ 乙：512，520，523，516，530，510，518，521，528，532，507，516，524，526，514.‎ ‎8‎ ‎87632‎ ‎87642200‎ ‎43‎ ‎50‎ ‎51‎ ‎52‎ ‎53‎ ‎7‎ ‎024668‎ ‎013468‎ ‎02‎ ‎(1).画出上述数据茎叶图；‎ ‎(2).试比较分析甲、乙两台机器生产零件的情况.‎ 解（1）用指标的两位数作茎，然后作茎叶图：‎ ‎（2）从图中可以看出，甲机器生产零件的指标 分布大致对称，指标平均在520左右，中位数 和众数均为522；乙机器生产零件的指标分布为 大致对称，指标平均在520左右，中位数和众数 分别为520和516，总的来看，甲机器生产的零 件的指标略大些..‎ 点评 注意作茎叶图时，茎可以放两位数.‎ 第3课 总体特征数的估计 ‎【考点导读】‎ 理解样本数据的方差、标准差的意义并且会计算数据的方差、标准差，使学生掌握通过合理抽样对总体稳定性作出科学的估计的思想.‎ ‎【基础练习】‎ ‎1．已知数据的平均数为，则数据，，…，的平均数为 22 .‎ ‎2．若M个数的平均数是X, N个数的平均数是Y,则这M+N个数的平均数是 ‎ ‎3．数据a1，a2，a3，…，an的方差为σ2，则数据2a1，2a2，2a3，…，2an的方差为 4σ2 .‎ ‎4．已知同一总体的两个样本，甲的样本方差为，乙的样本方差为，则下列说法正确的是 ④ .‎ ‎①甲的样本容量小 　　 ②乙的样本容量小　 ③甲的波动较小　　 ④乙的波动较小 ‎【范例解析】‎ 例1.下面是一个班在一次测验时的成绩，分别计算男生和女生的成绩平均值、中位数以及众数.试分析一下该班级学习情况.‎ 男生：55，55，61，65，68，68，71，72，73，74，75，78，80，81，82，87，94；‎ 女生：53，66，70，71，73，73，75，80，80，82，82，83，84，85，87，88，90，93，94，97.‎ 解：17名男生成绩的平均值是72.9分，中位数是73分，众数为55和68.‎ ‎20名女生成绩的平均值是80.3分，中位数是82分，众数为73，80和82.‎ 从上述情况来看，这个班女生成绩明显好于男生成绩.‎ 例2.为了比较甲，乙两位射击运动员的成绩，在相同的条件下对他们进行了10次测验，测得他们的环数如下：‎ 环数 ‎10‎ ‎9‎ ‎8‎ ‎7‎ ‎6‎ ‎5‎ 甲（次）‎ ‎3‎ ‎2‎ ‎1‎ ‎2‎ ‎0‎ ‎2‎ 乙（次）‎ ‎2‎ ‎2‎ ‎2‎ ‎2‎ ‎2‎ ‎0‎ 试根据以上数据，判断他们谁更优秀.‎ 解：=8,=8, =3.4,=2, 所以乙更优秀 例3．某化肥厂甲、乙两个车间包装肥料，在自动包装传送带上每隔30分钟抽取一包产品，‎ 称其重量，分别记录抽查数据如下：‎ 甲：102，101，99，98，103，98，99；‎ 乙：110，115，90，85，75，115，110．‎ ‎（1）这种抽样方法是哪一种方法？‎ ‎（2）计算甲、乙两个车间产品的平均数与方差，并说明哪个车间产品较稳定？‎ 解：（1）采用的方法是：系统抽样； ‎ ‎（2）；‎ ‎； ‎ ‎；‎ ‎∴ 故甲车间产品比较稳定．‎ 点评 以样本估计总体，在生产生活经常用到，发现问题，解决问题，从而更好地指导实践.‎ ‎【反馈演练】 ‎ ‎1. 下列说法中，正确的是 ④ .‎ ‎ ① 频率分布直方图中各小长方形的面积不等于相应各组的频率 ‎ ②一组数据的标准差是这组数据的方差的平方 ‎ ③数据2，3，4，5的方差是数据4，6，8，10的方差的一半 ‎ ④一组数据的方差越大，说明这组数据的波动越大 ‎2．从甲、乙两班分别任意抽出10名学生进行英语口语测验，其测验成绩的方差分别为S12= 13.2，S22=26．26，则 ① .‎ ‎①甲班10名学生的成绩比乙班10名学生的成绩整齐 ‎②乙班10名学生的成绩比甲班10名学生的成绩整齐 ‎③甲、乙两班10名学生的成绩一样整齐 ‎④不能比较甲、乙两班10名学生成绩的整齐程度 ‎3 ．已知样本为101 ,98, 102, 100, 99，则样本标准差为 ‎ ‎4 .某班45人，一次数学考试，班级均分72分.已知不及格人数为5人，他们的平均成绩是52分，则及格学生的平均分为 74 .5分 . ‎ ‎5．高三年级1000名学生进行数学其中测试.高三年级组随机调阅了100名学生的试卷（满分为150分），成绩记录如下：‎ 成绩（分）‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 人数 ‎6‎ ‎8‎ ‎10‎ ‎15‎ ‎15‎ ‎35‎ ‎8‎ ‎3‎ 求样本平均数和样本方差．‎ 解：=6.77‎ ‎ =3.1171‎ ‎6．两台机床同时生产直径为10的零件，为了检验产品质量，质量质检员从两台机床的产品中各抽取4件进行测量，结果如下：‎ 机床甲 ‎10‎ ‎9.8‎ ‎10‎ ‎10.2‎ 机床乙 ‎10.1‎ ‎10‎ ‎9.9‎ ‎10‎ 如果你是质量检测员，在收集到上述数据后，你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求.‎ 解：先考虑各自的平均数：设机床甲的平均数、方差分别为；机床乙的平均数、方差分别为.‎ ‎ ，‎ ‎∴两者平均数相同，再考虑各自的方差：‎ ‎∵，∴机床乙的零件质量更符合要求.‎ 第4课 案例分析 ‎【考点导读】‎ ‎1.会作两个有关联变量数据的散点图，并利用散点图直观认识变量间的相关关系.‎ ‎2.知道最小二乘法的思想，能根据给出的线性回归方程系数公式建立线性回归方程.‎ ‎3.了解独立性检验的基本思想、方法及其初步应用，了解回归与分析的基本思想、方法及其初步应用.‎ ‎【基础练习】‎ ‎1．根据下表中的数据：可求出与的线性回归方程是 ‎ ‎ ‎ x ‎-1‎ ‎0‎ ‎1‎ ‎2‎ y ‎-1‎ ‎0‎ ‎1‎ ‎1‎ ‎2．线性回归方程表示的直线必经过的一个定点是 ‎ ‎3．设有一个直线回归方程为 ,则变量x 增加一个单位时 ③ .‎ ‎① y 平均增加 1.5 个单位 ② y 平均增加 2 个单位 ‎ ③ y 平均减少 1.5 个单位 ④ y 平均减少 2 个单位 ‎4．对于给定的两个变量的统计数据，下列说法正确的是 ③ .‎ ‎①都可以分析出两个变量的关系 ②都可以用一条直线近似地表示两者的关系 ‎③都可以作出散点图 ④都可以用确定的表达式表示两者的关系 ‎5．对于两个变量之间的相关系数，下列说法中正确的是 ③ . ‎ ‎①|r|越大，相关程度越大 ‎②|r|，|r|越大，相关程度越小，|r|越小，相关程度越大 ‎③|r|1且|r|越接近于1，相关程度越大；|r|越接近于0，相关程度越小 ‎【范例解析】‎ 例1．在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人．女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动．‎ ‎（1）根据以上数据建立一个2×2的列联表；（2）判断性别与休闲方式是否有关系．‎ 解：（1）2×2的列联表 性别 休闲方式 看电视 运动 总计 女 ‎43‎ ‎27‎ ‎70‎ 男 ‎21‎ ‎33‎ ‎54‎ 总计 ‎64‎ ‎60‎ ‎124‎ ‎（2）假设“休闲方式与性别无关”‎ 计算 ‎ 因为，所以有理由认为假设“休闲方式与性别无关”是不合理的，‎ 即有97.5%的把握认为“休闲方式与性别有关”.‎ 点评 对两个变量相关性的研究，可先计算的值，并根据临界表进行估计与判断.‎ 例3. 一个车间为了为了规定工时定额，需要确定加工零件所花费的时间，为此进行了10次实验，测得如下数据：‎ 零件数x (个)‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ ‎70‎ ‎80‎ ‎90‎ ‎100‎ 加工时间y(分)‎ ‎62‎ ‎68‎ ‎75‎ ‎81‎ ‎89‎ ‎95‎ ‎102‎ ‎108‎ ‎115‎ ‎122‎ (1) y与x是否具有线性相关关系？‎ (2) 如果y与x具有线性相关关系，求回归直线方程；‎ (3) 据此估计加工200个零件所用时间为多少？‎ 解：（1）查表可得0.05和n-2相关系数临界，‎ 由知y与x具有线性相关关系.‎ ‎（2）回归直线方程为 ‎ ‎（3）估计加工200个零件所用时间189分.‎ ‎【反馈演练】 ‎ ‎1．下列两个变量之间的关系不是函数关系的是 ④ . ‎ ‎①角度与它的余弦值 ②正方形的边长与面积 ‎③正n边形的边数和顶点角度之和 ④人的年龄与身高 ‎2．为了考察两个变量x和y之间的线性相关性，甲、乙两个同学各自独立的做10次和15次试验，并且 利用线性回归方法，求得回归直线分布为和，已知在两人的试验中发现对变量x的观察数据的平均值 恰好相等都为s，对变量y的观察数据的平均值恰好相等都为t,那么下列说法正确的是 ① . ‎ ‎①直线和有交点（s,t） ②直线和相交，但是交点未必是（s,t）‎ ‎③ 直线和平行 ④ 直线和必定重合 ‎3．下列两个变量之间的关系是相关关系的是 ④ . ‎ ‎①正方体的棱长和体积 ②单位圆中角的度数和所对弧长 ‎③单产为常数时，土地面积和总产量 ④日照时间与水稻的亩产量 ‎4．对于回归方程y=4.75x+257,当x=28时,y的估计值为 390 .‎ ‎5．某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：‎ 性别 专业 非统计专业 统计专业 男 ‎13‎ ‎10‎ 女 ‎7‎ ‎20‎ 为了判断主修统计专业是否与性别有关系，根据 表中的数据，得到，因为，所以判定主修统计专业与性别有关系，那么这种判断出错的可能性为 5% .‎ ‎6.为了研究失重情况下男女飞行员晕飞船的情况，抽取了89名被试者，他们的晕船情况汇总如下表，根据独立性假设检验的方法， 不能 认为在失重情况下男性比女性更容易晕船（填能或不能） ‎ 晕机 不晕机 合计 男性 ‎23‎ ‎32‎ ‎55‎ 女性 ‎9‎ ‎25‎ ‎34‎ 合计 ‎32‎ ‎57‎ ‎89‎ ‎7.打鼾不仅影响别人休息，而且可能与患某种疾病有关，下表是一次调查所得的数据，试问：每一晚都打鼾与患心脏病有关吗？‎ 患心脏病 未患心脏病 合计 每一晚都打鼾 ‎30‎ ‎224‎ ‎254‎ 不打鼾 ‎24‎ ‎1355‎ ‎1379‎ 合计 ‎54‎ ‎1579‎ ‎1633‎ 解：提出假设H0：打鼾与患心脏病无关，根据数据得 ‎ 当H0成立时，的概率为1%，而这时 所以我们有99%的把握认为打鼾与患心脏病有关.‎ 第5课 古典概型 ‎【考点导读】 ‎ ‎1.在具体情境中，了解随机事件发生的不确定性及频率的稳定性，进一步了解概率的意义以及概率与频率的区别.‎ ‎2.正确理解古典概型的两大特点：1）试验中所有可能出现的基本事件只有有限个；2）每个基本事件出现的可能性相等.‎ ‎【基础练习】‎ ‎1. 某射手在同一条件下进行射击，结果如下表所示：‎ 射击次数n ‎10‎ ‎20‎ ‎50‎ ‎100‎ ‎200‎ ‎500‎ 击中靶心次数m ‎8‎ ‎19‎ ‎44‎ ‎92‎ ‎178‎ ‎455‎ 击中靶心的频率 ‎（1）填写表中击中靶心的频率；‎ ‎（2）这个射手射击一次，击中靶心的概率约是什么？‎ 分析：事件A出现的频数nA与试验次数n的比值即为事件A的频率，当事件A发生的频率fn（A）稳定在某个常数上时，这个常数即为事件A的概率.‎ 解：（1）表中依次填入的数据为：0.80，0.95，0.88，0.92，0.89，0.91.‎ ‎（2）由于频率稳定在常数0.89，所以这个射手击一次，击中靶心的概率约是0.89.‎ 点评 概率实际上是频率的科学抽象，求某事件的概率可以通过求该事件的频率而得之.‎ ‎2．将一枚硬币向上抛掷10次，其中正面向上恰有5次是 随机 事件 （必然、随机、不可能）‎ ‎3．下列说法正确的是 ③ .‎ ‎①任一事件的概率总在（0.1）内 ②不可能事件的概率不一定为0‎ ‎③必然事件的概率一定为1 ④以上均不对 ‎4.一枚硬币连掷3次，只有一次出现正面的概率是 ‎ ‎5. 从分别写有A、B、C、D、E的5张卡片中，任取2张，这2张卡片上的字母恰好是按字母顺序相邻的概率为 ‎ ‎【范例解析】‎ 例1. 连续掷3枚硬币，观察落地后这3枚硬币出现正面还是反面.‎ ‎（1）写出这个试验的基本事件；‎ ‎（2）求这个试验的基本事件的总数；‎ ‎（3）“恰有两枚正面向上”这一事件包含哪几个基本事件?‎ 解：（1）这个试验的基本事件Ω={（正，正，正），（正，正，反），（正，反，正），（正，反，反），（反，正，正），（反，正，反），（反，反，正），（反，反，反）}；‎ ‎（2）基本事件的总数是8.‎ ‎（3）“恰有两枚正面向上”包含以下3个基本事件：（正，正，反），（正，反，正），（反，正，正）.‎ 点评 一次试验中所有可能的结果都是随机事件，这类随机事件称为基本事件.‎ 例2. 抛掷两颗骰子，求：‎ ‎（1）点数之和出现7点的概率；‎ ‎（2）出现两个4点的概率.‎ 解：作图，从下图中容易看出基本事件空间与点集S={（x，y）|x∈N，y∈N，1≤x≤6，1≤y≤6}中的元 素一一对应.因为S中点的总数是6×6=36（个），所以基本事件总数n=36.‎ ‎（1）记“点数之和出现7点”的事件为A，从图中可看到事件A包含的基本事件数共6个：（6，1），（5，2），（4，3），（3，4），（2，5），（1，6），所以P（A）=.‎ ‎（2）记“出现两个4点”的事件为B，则从图中可看到事件B包含的基本事件数只有1个：（4，4）.所以P（B）=.‎ 点评 在古典概型下求P（A），关键要找出A所包含的基本事件个数然后套用公式 变题 .在一次口试中，考生要从5道题中随机抽取3道进行回答，答对其中2道题为优秀，答对其中1道题为及格，某考生能答对5道题中的2道题，试求：‎ ‎（1）他获得优秀的概率为多少；‎ ‎（2）他获得及格及及格以上的概率为多少；‎ 点拨：这是一道古典概率问题，须用枚举法列出基本事件数.‎ 解：设这5道题的题号分别为1,2，3，4，5，则从这5道题中任取3道回答，有（1，2，3），（1，2，4），（1，2，5），（1，3，4），（1，3，5），（1，4，5），（2，3，4）,（2，3，5），‎ ‎（2，4，5），（3，4，5）共10个基本事件． ‎ ‎（1）记“获得优秀”为事件A，则随机事件A中包含的基本事件个数为3，故．‎ ‎（2）记“获得及格及及格以上”为事件B，则随机事件B中包含的基本事件个数为9，故．‎ 点评：使用枚举法要注意排列的方法，做到不漏不重.‎ 例3. 从含有两件正品a1，a2和一件次品b1的三件产品中，每次任取一件，每次取出后不放回，连续取两 次，求取出的两件产品中恰有一件次品的概率.‎ 解：每次取出一个，取后不放回地连续取两次，其一切可能的结果组成的基本事件有6个，即（a1，a2），（a1，b2），（a2，a1），（a2，b1），（b1，a1），（b2，a2）.其中小括号内左边的字母表示第1次取出的产品，‎ 右边的字母表示第2次取出的产用A表示“取出的两种中，恰好有一件次品”这一事件，则 A=[（a1，b1），（a2，b1），（b1，a1），（b1，a2）] 事件A由4个基本事件组成，因而，P（A）==‎ ‎【反馈演练】 ‎ ‎1.某人进行打靶练习，共射击10次，其中有2次中10环，有3次环中9环，有4次中8环，有1次未中靶，试计算此人中靶的概率，假设此人射击1次，试问中靶的概率约为 0.9 中10环的概率约为 0.2 .‎ 分析：中靶的频数为9，试验次数为10，所以中靶的频率为=0.9，所以中靶的概率约为0.9．‎ 解：此人中靶的概率约为0.9；此人射击1次，中靶的概率为0.9；中10环的概率约为0.2．‎ ‎2.一栋楼房有4个单元，甲乙两人被分配住进该楼，则他们同住一单元的概率是 0.25 .‎ ‎3. 在第1,3,6,8,16路公共汽车都要停靠的一个站（假定这个站只能停靠一辆汽车），有一位乘客等候第6‎ 路或第16路汽车.假定当时各路汽车首先到站的可能性相等，则首先到站正好是这位乘客所需乘的汽车的 概率等于 ‎ ‎4.把三枚硬币一起抛出，出现2枚正面向上，一枚反面向上的概率是 ‎ ‎5.有5根细木棒，长度分别为1,3 ,5 ,7 ,9，从中任取三根，能搭成三角形的概率是 ‎ ‎6. 从1，2，3，…，9这9个数字中任取2个数字， ‎ ‎（1）2个数字都是奇数的概率为 ‎ ‎（2）2个数字之和为偶数的概率为 ‎ ‎7. 某小组共有10名学生，其中女生3名，现选举2名代表，至少有1名女生当选的概率为 ‎ ‎8. A、B、C、D、E排成一排，A在B的右边（A、B可以不相邻）的概率是 ‎ ‎9．在大小相同的5个球中，2个是红球，3个是白球，若从中任取2个，则所取的2个球中至少有一个红球的概率是 ‎ ‎10. 用红、黄、蓝三种不同颜色给下图中3个矩形随机涂色，每个矩形只涂一种颜色，求：‎ ‎（1）3个矩形颜色都相同的概率；（2）3个矩形颜色都不同的概率.‎ 解：所有可能的基本事件共有27个，如图所示.‎ ‎（1）记“3个矩形都涂同一颜色”为事件A，由图知，事件A的基本事件有1×3=3个，故P（A）=.‎ ‎（2）记“3个矩形颜色都不同”为事件B，由图可知，事件B的基本事件有2×3=6个，故P（B）=.‎ ‎11. 甲、乙两个均匀的正方体玩具，各个面上分别刻有1，2，3，4，5，6六个数字，将这两个玩具同时 掷一次.‎ ‎（1）若甲上的数字为十位数，乙上的数字为个位数，问可以组成多少个不同的数，其中个位数字与十位数字均相同的数字的概率是多少?‎ ‎（2）两个玩具的数字之和共有多少种不同结果?其中数字之和为12的有多少种情况?数字之和为6的共有多少种情况?分别计算这两种情况的概率.‎ 解：（1）甲有6种不同的结果，乙也有6种不同的结果，故基本事件总数为6×6=36个.其中十位数字共有6种不同的结果，若十位数字与个位数字相同，十位数字确定后，个位数字也即确定.故共有6×1=6种不同的结果，即概率为.‎ ‎（2）两个玩具的数字之和共有2，3，4，5，6，7，8，9，10，11，12共11种不同结果.从中可以看出，出现12的只有一种情况，概率为.出现数字之和为6的共有（1，5），（2，4），（3，3），（4，2），（5，1）五种情况，所以其概率为.‎ ‎12.现有一批产品共有10件，其中8件为正品，2件为次品：‎ ‎（1）如果从中取出一件，然后放回，再取一件，求连续3次取出的都是正品的概率；‎ ‎（2）如果从中一次取3件，求3件都是正品的概率．‎ 解：（1）有放回地抽取3次，按抽取顺序（x,y,z）记录结果，则x,y,z都有10种可能，所以试验结果有 ‎10×10×10=103种；设事件A为“连续3次都取正品”，则包含的基本事件共有8×8×8=83种，‎ 因此，P(A)= =0.512．‎ ‎（2）可以看作不放回抽样3次，顺序不同，基本事件不同，按抽取顺序记录（x,y,z），则x有10种可能，y有9种可能，z有8种可能，所以试验的所有结果为10×9×8=720种．设事件B为“3件都是正品”，则事件B包含的基本事件总数为8×7×6=336, 所以P(B)= ．‎ 第6课几何概型 ‎【考点导读】‎ ‎1．了解几何概型的基本特点.‎ ‎2．会进行简单的几何概率的计算.‎ ‎【基础练习】‎ ‎1．在500ml的水中有一个草履虫，现从中随机取出2ml水样放到显微镜下观察，则发现草履虫的概率是 ‎ ‎ 0.004 ‎ ‎2. 取一根长度为3 m的绳子，拉直后在任意位置剪断，那么剪得两段的长都不小于1 m的概率是 ‎ ‎3. 在1万 km2的海域中有40 km2的大陆架贮藏着石油，假如在海域中任意一点钻探，钻到油层面的概率 是 ‎ ‎(第5题)‎ ‎4. 如下图，在一个边长为3 cm的正方形内部画一个边长为2 cm的正方形，向大正方形内随机投点，则所投的点落入小正方形内的概率是 .‎ ‎(第4题)‎ ‎ ‎ ‎5. 如下图，在直角坐标系内，射线OT落在60°的终边上，任作一条射线OA，则射线落在∠xOT内的概率是 .‎ ‎【范例解析】‎ 例1. 在等腰Rt△ABC中， (1)在斜边AB上任取一点M，求AM的长小于AC的长的概率.‎ ‎（2）过直角顶点C在内作一条射线CM，与线段AB交于点M，求AM