- 160.04 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
32 二元一次不等式(组)与简单的线性规划问题
1.不等式-x2+3x-2>0的解集是 ( )
A.{x|x<-2或x>-1} B.{x|x<1或x>2}
C.{x|10,即x2-3x+2<0,(x-1)(x-2)<0,解得10,所以x<-1或x>1.
3.(2019·唐山模拟)下列命题中,正确的是 ( )
A.若a>b,c>d,则ac>bd
B.若ac>bc,则a>b
C.若1a<1b<0,则|a|+b<0
D.若a>b,c>d,则a-c>b-d
【解析】选C.取a=2,b=1,c=-1,d=-2,可知A错误;当c<0时,ac>bc⇒a-a>0,故-b>|a|,即|a|+b<0,故C正确;取a=c=2,b=d=1,可知D错误.
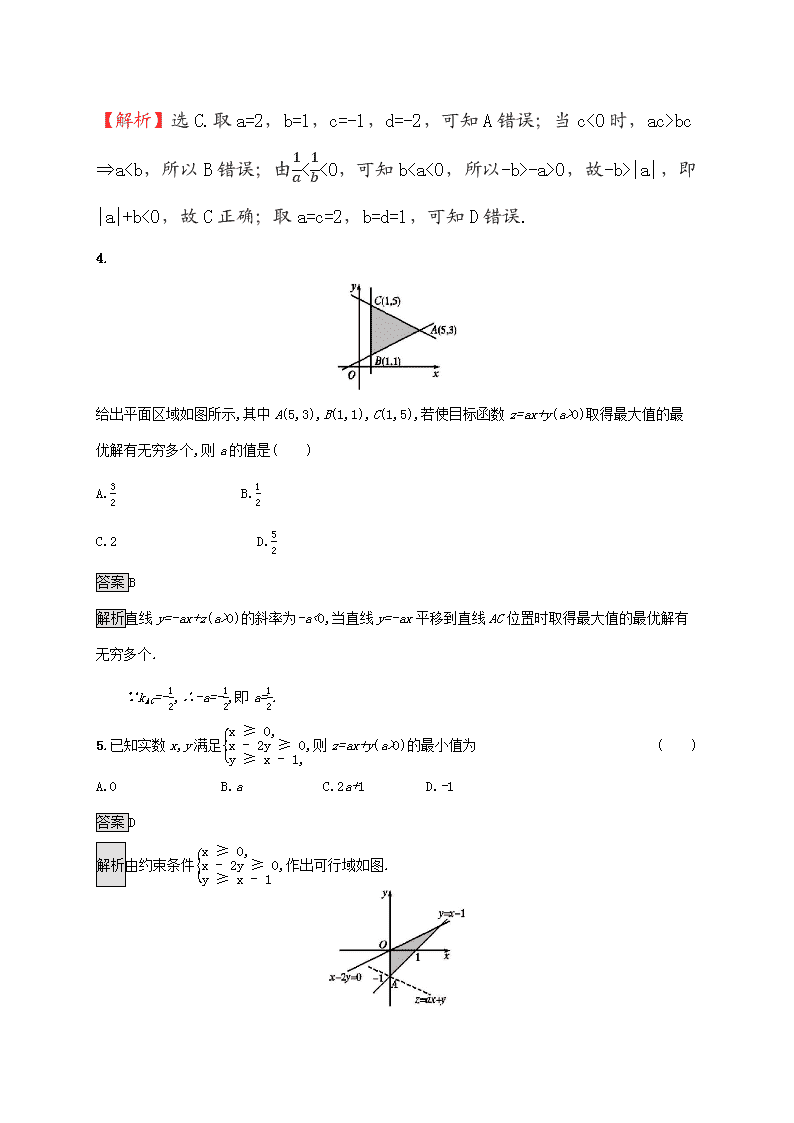
4.
给出平面区域如图所示,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值是( )
A.32 B.12
C.2 D.52
答案B
解析直线y=-ax+z(a>0)的斜率为-a<0,当直线y=-ax平移到直线AC位置时取得最大值的最优解有无穷多个.
∵kAC=-12,∴-a=-12,即a=12.
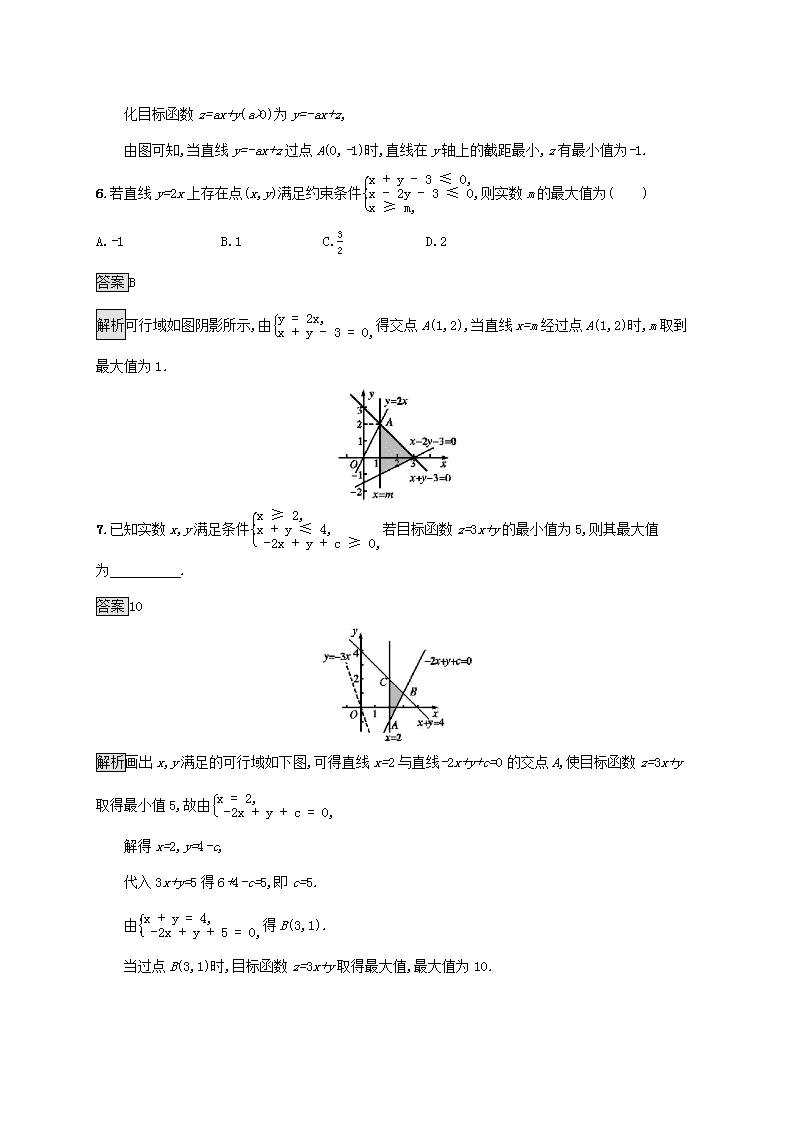
5.已知实数x,y满足x≥0,x-2y≥0,y≥x-1,则z=ax+y(a>0)的最小值为( )
A.0 B.a C.2a+1 D.-1
答案D
解析由约束条件x≥0,x-2y≥0,y≥x-1作出可行域如图.
化目标函数z=ax+y(a>0)为y=-ax+z,
由图可知,当直线y=-ax+z过点A(0,-1)时,直线在y轴上的截距最小,z有最小值为-1.
6.若直线y=2x上存在点(x,y)满足约束条件x+y-3≤0,x-2y-3≤0,x≥m,则实数m的最大值为( )
A.-1 B.1 C.32 D.2
答案B
解析可行域如图阴影所示,由y=2x,x+y-3=0,得交点A(1,2),当直线x=m经过点A(1,2)时,m取到最大值为1.
7.已知实数x,y满足条件x≥2,x+y≤4,-2x+y+c≥0,若目标函数z=3x+y的最小值为5,则其最大值为 .
答案10
解析画出x,y满足的可行域如下图,可得直线x=2与直线-2x+y+c=0的交点A,使目标函数z=3x+y取得最小值5,故由x=2,-2x+y+c=0,
解得x=2,y=4-c,
代入3x+y=5得6+4-c=5,即c=5.
由x+y=4,-2x+y+5=0,得B(3,1).
当过点B(3,1)时,目标函数z=3x+y取得最大值,最大值为10.
8.某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨、B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨.销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨,则该企业可获得的最大利润是 万元.
答案27
解析设生产甲产品x吨、乙产品y吨,则获得的利润为z=5x+3y.
由题意得x≥0,y≥0,3x+y≤13,2x+3y≤18,此不等式组表示的平面区域如图阴影部分所示.
由图可知当y=-53x+z3经过点A时,z取得最大值,此时x=3,y=4,zmax=5×3+3×4=27(万元).
9.已知实数x,y满足x-2y+4≥0,2x+y-2≥0,3x-y-3≤0,则x2+y2的取值范围是 .
答案45,13
解析画出约束条件对应的可行域(如图中阴影部分所示),x2+y2表示原点到可行域中的点的距离的平方,由图知原点到直线2x+y-2=0的距离的平方为x2+y2的最小值,为252=45,原点到点(2,3)的距离的平方为x2+y2的最大值,为22+32=13.
因此x2+y2的取值范围是45,13.
10.已知x,y满足约束条件x+y-2≤0,x-2y-2≤0,2x-y+2≥0.若z=y-ax取得最大值的最优解不唯一,则实数a的值为( )
A.12或-1 B.2或12
C.2或1 D.2或-1
答案D
解析(方法一)由题中条件画出可行域如图中阴影部分所示,
可知A(0,2),B(2,0),C(-2,-2),
则zA=2,zB=-2a,zC=2a-2,
要使目标函数取得最大值的最优解不唯一,只要zA=zB>zC或zA=zC>zB或zB=zC>zA,解得a=-1或a=2.
(方法二)目标函数z=y-ax可化为y=ax+z,令l0:y=ax,平移l0,则当l0∥AB或l0∥AC时符合题意,
故a=-1或a=2.
11.若不等式组x+y-2≤0,x+2y-2≥0,x-y+2m≥0表示的平面区域为三角形,且其面积等于43,则m的值为( )
A.-3 B.1 C.43 D.3
答案B
解析如图,要使不等式组表示的平面区域为三角形,则不等式x-y+2m≥0表示的平面区域为直线x-y+2m=0下方的区域,且-2m<2,即m>-1.这时平面区域为△ABC.
由x+y-2=0,x+2y-2=0,解得x=2,y=0,则A(2,0).
由x+y-2=0,x-y+2m=0,解得x=1-m,y=1+m,则B(1-m,1+m).
同理C2-4m3,2+2m3,M(-2m,0).
S△ABC=S△ABM-S△ACM
=12·(2+2m)·(1+m)-2+2m3=(m+1)23,
由已知得(m+1)23=43,解得m=1(m=-3<-1舍去).
12.某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的质量(单位:吨)如下表所示:
原料
肥料
A
B
C
甲
4
8
3
乙
5
5
10
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数量.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
解(1)由已知,x,y满足的数学关系式为4x+5y≤200,8x+5y≤360,3x+10y≤300,x≥0,y≥0.该二元一次不等式组所表示的平面区域为图1中的阴影部分:
图1
图2
(2)设利润为z万元,则目标函数为z=2x+3y.
考虑z=2x+3y,将它变形为y=-23x+z3,这是斜率为-23,随z变化的一族平行直线,z3为直线在y轴上的截距,当z3取最大值时,z的值最大.又因为x,y满足约束条件,所以由图2可知,当直线z=2x+3y经过可行域上的点M时,截距z3最大,即z最大.
解方程组4x+5y=200,3x+10y=300,得点M的坐标为(20,24).
所以zmax=2×20+3×24=112.
答:生产甲种肥料20车皮、乙种肥料24车皮时利润最大,且最大利润为112万元.
三、高考预测
13.已知x,y满足约束条件x-y+2≥0,x≤1,x+y+k≥0,z=x+3y的最大值是最小值的-2倍,则k= .
答案1
解析画出不等式组表示的平面区域,如图所示,
结合目标函数的几何意义可知,目标函数在点C(1,3)处取得最大值,在点B(1,-1-k)处取得最小值,
所以zmax=1+3×3=10,zmin=1+3×(-1-k)=-2-3k.
根据题意有10=-2(-2-3k),解得k=1.