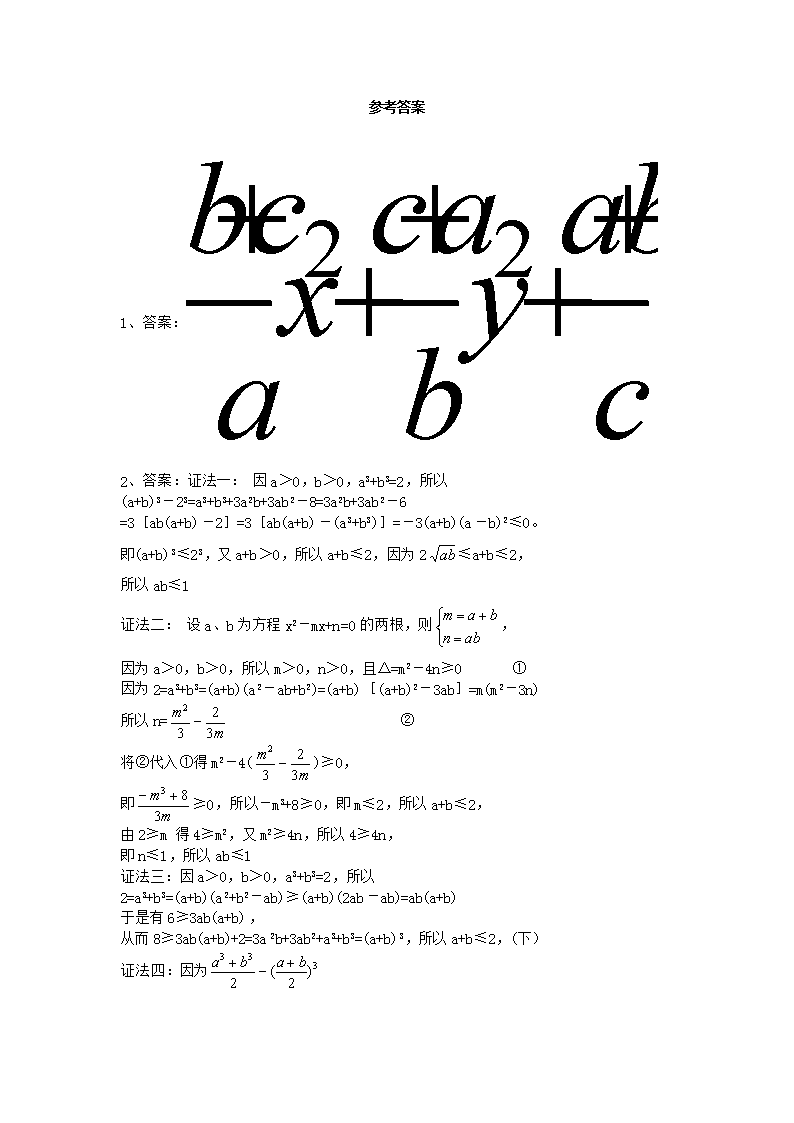【数学】2020届一轮复习人教A版 证明不等式的基本方法 课时作业 10页

‎2020届一轮复习人教A版 证明不等式的基本方法 课时作业 ‎ 1、证明下列不等式:‎ ‎(1)若x，y，z∈R，a，b，c∈R+，则z2≥2(xy+yz+zx)‎ ‎(2)若x，y，z∈R+，且x+y+z=xyz，则≥2() 2、若a＞0，b＞0，a3+b3=2，求证： a+b≤2，ab≤1。 3、已知i，m、n是正整数，且1＜i≤m＜n.‎ ‎(1)证明: niA＜miA ‎ ‎(2)证明: (1+m)n＞(1+n)m 4、已知：，求证：‎ ‎（Ⅰ）.‎ ‎（Ⅱ）. 5、设，求证：。 6、设a、b、c均为实数，求证：++≥++‎ ‎7、设a,b,c为正实数.求证：+abc≥2. 8、若a,b∈R,求证：≤+. 9、设a,b,c都是正数，求证：‎ ‎（1）（a+b+c)≥9;‎ ‎(2)(a+b+c) ≥. 10、已知x1,x2,…,xn都是正数，且x1+x2+…+xn=1,求证： ++…+≥n2. 11、已知|a|＜1,|b|＜1,求证：＜1. 12、已知x＞0,y＞0,z＞0.求证：≥8. 13、已知,a,b,c均为正数，且a+b+c=1.求证：++≥9. 14、已知a、b∈（0，+∞），且a+b=1,求证：‎ ‎(1)a2+b2≥;‎ ‎(2)+≥8;‎ ‎(3)+ ≥;‎ ‎(4) ≥. 15、设a＞0,b＞0,a+b=1.‎ ‎（1）证明：ab+≥4;‎ ‎（2）探索猜想，并将结果填在以下括号内：‎ a2b2+≥（ ）；a3b3+≥（ ）；‎ ‎（3）由（1）（2）归纳出更一般的结论，并加以证明. 16、定义：对于函数,.若对定义域内的恒成立,则称函数为函数.(1)请举出一个定义域为的函数,并说明理由;(2)对于定义域为的函数，求证：对于定义域内的任意正数，均有;‎ ‎(3)对于值域的函数,求证：. 17、已知x，y均为正数，且x＞y，求证：． 18、已知，且，求证： 19、已知，求证：。 20、已知都是实数，求证 参考答案 ‎1、答案： 2、答案：证法一： 因a＞0，b＞0，a3+b3=2，所以 ‎(a+b)3－23=a3+b3+3a2b+3ab2－8=3a2b+3ab2－6‎ ‎=3［ab(a+b)－2］=3［ab(a+b)－(a3+b3)］=－3(a+b)(a－b)2≤0。 ‎ 即(a+b)3≤23，又a+b＞0，所以a+b≤2，因为2≤a+b≤2，‎ 所以ab≤1 ‎ 证法二： 设a、b为方程x2－mx+n=0的两根，则，‎ 因为a＞0，b＞0，所以m＞0，n＞0，且Δ=m2－4n≥0 ①‎ 因为2=a3+b3=(a+b)(a2－ab+b2)=(a+b)［(a+b)2－3ab］=m(m2－3n)‎ 所以n= ②‎ 将②代入①得m2－4()≥0，‎ 即≥0，所以－m3+8≥0，即m≤2，所以a+b≤2，‎ 由2≥m 得4≥m2，又m2≥4n，所以4≥4n，‎ 即n≤1，所以ab≤1 ‎ 证法三：因a＞0，b＞0，a3+b3=2，所以 ‎2=a3+b3=(a+b)(a2+b2－ab)≥(a+b)(2ab－ab)=ab(a+b)‎ 于是有6≥3ab(a+b)，‎ 从而8≥3ab(a+b)+2=3a2b+3ab2+a3+b3=(a+b)3，所以a+b≤2，(下）‎ 证法四：因为 ‎≥0，‎ 所以对任意非负实数a、b，有≥‎ 因为a＞0，b＞0，a3+b3=2，所以1=≥，‎ ‎∴≤1，即a+b≤2，(以下）‎ 证法五： 假设a+b＞2，则 a3+b3=(a+b)(a2－ab+b2)=(a+b)［(a+b)2－3ab］＞(a+b)ab＞2ab，所以ab＜1，‎ 又a3+b3=(a+b)［a2－ab+b2］=(a+b)［(a+b)2－3ab］＞2(22－3ab)‎ 因为a3+b3=2，所以2＞2(4－3ab)，因此ab＞1，前后矛盾，‎ 故a+b≤2(以下)。 3、答案：(1)对于1＜i≤m，且A =m·…·(m－i+1)，‎ ‎，‎ 由于m＜n，对于整数k=1，2，…，i－1，有，‎ 所以 ‎(2)由二项式定理有：‎ ‎(1+m)n=1+Cm+Cm2+…+Cmn，‎ ‎(1+n)m=1+Cn+Cn2+…+Cnm，‎ 由(1)知miA＞niA (1＜i≤m，而C=‎ ‎∴miCin＞niCim(1＜m＜n ‎∴m0C=n0C=1，mC=nC=m·n，m2C＞n2C，…，‎ mmC＞nmC，mm+1C＞0，…，mnC＞0，‎ ‎∴1+Cm+Cm2+…+Cmn＞1+Cn+C2mn2+…+Cnm，‎ 即(1+m)n＞(1+n)m成立。 4、答案：（Ⅰ）∵，，， ‎ ‎∴， ‎ ‎∵，‎ ‎∴，‎ ‎∴. ‎ ‎（Ⅱ）∵， ‎ ‎∴. 5、答案：因为，所以有。又，故有。‎ 于是有 得证。 6、答案：∵a、b、c均为实数．‎ ‎∴（＋）≥≥，当a=b时等号成立； ‎ ‎（＋）≥≥，当b=c时等号成立； ‎ ‎（＋）≥≥． ‎ 三个不等式相加即得++≥++，‎ 当且仅当a=b=c时等号成立. 7、答案：因为a,b,c是正实数，由平均不等式可得 ‎≥3，‎ 即≥，‎ 所以+abc≥+abc.‎ 而+abc≥2=2,‎ 所以+abc≥2. 8、答案：当|a+b|=0时，不等式显然成立.‎ 当|a+b|≠0时，由0＜|a+b|≤|a|+|b|‎ ‎≥,‎ 所以=‎ ‎≤‎ ‎=‎ ‎≤+. 9、答案：（1）∵a,b,c都是正数，‎ ‎∴a+b+c≥3,++≥3.‎ ‎∴(a+b+c) ≥9,‎ 当且仅当a=b=c时，等号成立.‎ ‎（2）∵（a+b）+(b+c)+(c+a)‎ ‎≥3,‎ 又≥,‎ ‎∴(a+b+c) ≥,‎ 当且仅当a=b=c时，等号成立. 10、答案： ++…+=(x1+x2+…+xn)（ ++…+）‎ ‎≥=n2. 11、答案：∵＜1＜1‎ a2+b2+2ab＜1+2ab+a2b2‎ a2b2-a2-b2+1＞0‎  (a2-1)(b2-1)＞0‎ 又|a|＜1,|b|＜1,∴(a2-1)(b2-1)＞0.‎ ‎∴原不等式成立. 12、答案：∵x＞0,y＞0,z＞0,‎ ‎∴+≥＞0, +≥＞0.‎ ‎+≥＞0,‎ ‎∴ ‎ ‎≥=8.‎ ‎（当且仅当x=y=z时等号成立） 13、答案：++= ++‎ ‎=3+++‎ ‎≥3+2+2+2=9.‎ 当且仅当a=b=c=时取等号. 14、答案：(1)∵a2+b2=(a+b)2-2ab=1-2ab≥1-2×=，‎ ‎∴a2+b2≥.‎ ‎(2)∵+≥≥8,∴+≥8.‎ ‎(3)由(1)、(2)的结论，知 ‎+ =a2+b2+4++‎ ‎≥+4+8=,∴+ ≥.‎ ‎ (4) =++ab+‎ ‎=+++2≥2++2=. 15、答案：（1）证明 方法一 ab+≥44a2b2-17ab+4≥0‎ (4ab-1)(ab-4)≥0.‎ ‎∵ab=()2≤=,‎ ‎∴4ab≤1，而又知ab≤＜4,‎ 因此（4ab-1）(ab-4)≥0成立，故ab+≥4.‎ 方法二 ab+=ab++，‎ ‎∵ab≤=，∴≥4，∴≥.‎ 当且仅当a=b=时取等号.‎ 又ab+≥2=，‎ 当且仅当ab=，即=4,a=b=时取等号.‎ 故ab+≥+=4‎ ‎（当且仅当a=b=时，等号成立）.‎ ‎（2）解 猜想：当a=b=时，‎ 不等式a2b2+≥( )与a3b3+≥( )取等号，故在括号内分别填16与64.‎ ‎（3）解 由此得到更一般性的结论：‎ anbn+≥4n+.‎ 证明如下：‎ ‎∵ab≤=,∴≥4.‎ ‎∴anbn+=anbn++‎ ‎≥2+×4n ‎=+=4n+，‎ 当且仅当ab=,即a=b=时取等号. 16、答案：（1）如函数就是定义域内的函数.‎ 下面进行证明: 必定成立.‎ ‎（2）构造函数，，‎ 即在R上递增所以，‎ ‎，…‎ 得到，，‎ ‎…‎ 相加后，得到：‎ ‎（3）构造函数，则，因为，所以 得到有 所以，…，‎ 所以有 17、答案：因为x＞0，y＞0，x－y＞0，‎ ‎= ， ‎ 所以． 18、答案：∵‎ ‎--6分 ‎　又 ‎ ‎ ∴‎ 故 19、答案：因为 20、答案：不妨设，则 ‎ 在中，由三角形三边之间的关系知：‎ ‎ 当且仅当O在AB上时，等号成立。‎ ‎ 因此， ‎