安徽省皖南八校2021届高三数学（文）上学期第二次联考试题（Word版附答案） 13页

“皖南八校”2021 届高三第二次联考 数学（文科） 2020.12 考生注意： 1．本试卷满分 150 分，考试时间 120 分钟． 2．考生作答时，请将答案答在答题卡上．选择题每小题选出答案后，用 2B 铅笔把答题卡上 对应题目的答案标号涂黑；非选择题请用直径 0.5 毫米黑色墨水签字笔在答题卡上各题的答题 区域内作答，超出答题区域书写的答案无效．．．．．．．．．．．．．，在试题卷．．．．、草稿纸上作答无效．．．．．．．．． 3．做选考题时，考生须按照题目要求作答，并用 2B 铅笔在答题卡上把所选題目的题号涂黑． 一、选择题：本题共 12 小题；每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一 项是符合题目要求的． 1．已知集合 2 1| 4A x x    „ ，集合  2| 1B y y x   ，则 A B （ ） A． 1 1,2 2     B． 1 ,12     C． 1 ,2     D． 10, 2      2．若复数 z 满足 (1 3 )z i i  ，则复数 z 的虚部为（ ） A．1 B．2 C．i D． 2i 3．已知 1 3 2 3 12 , log , log 23a b c   ，则（ ） A． a b c  B． c a b  C． c b a  D． a c b  4．若等差数列 na 各项都是正数， 1 2 3 21a a a   ，且 3 4 5 45a a a   ，则 1a 的值为（ ） A．4 B．3 C．6 D．2 5．执行如下图所示的程序框图，若输出的 120S  ，则判断框内应填入的条件是（ ） A． 4?k  B． 5?k  C． 6?k  D． 7?k  6．如图所示，在边长为 2 的正三角形中有一封闭曲线围成的阴影区域．在正三角形中随机撒一粒豆子，它 落在阴影区域内的概率为 4 5 ，则阴影区域的面积为（ ） A． 3 5 B． 2 3 5 C． 3 3 5 D． 4 3 5 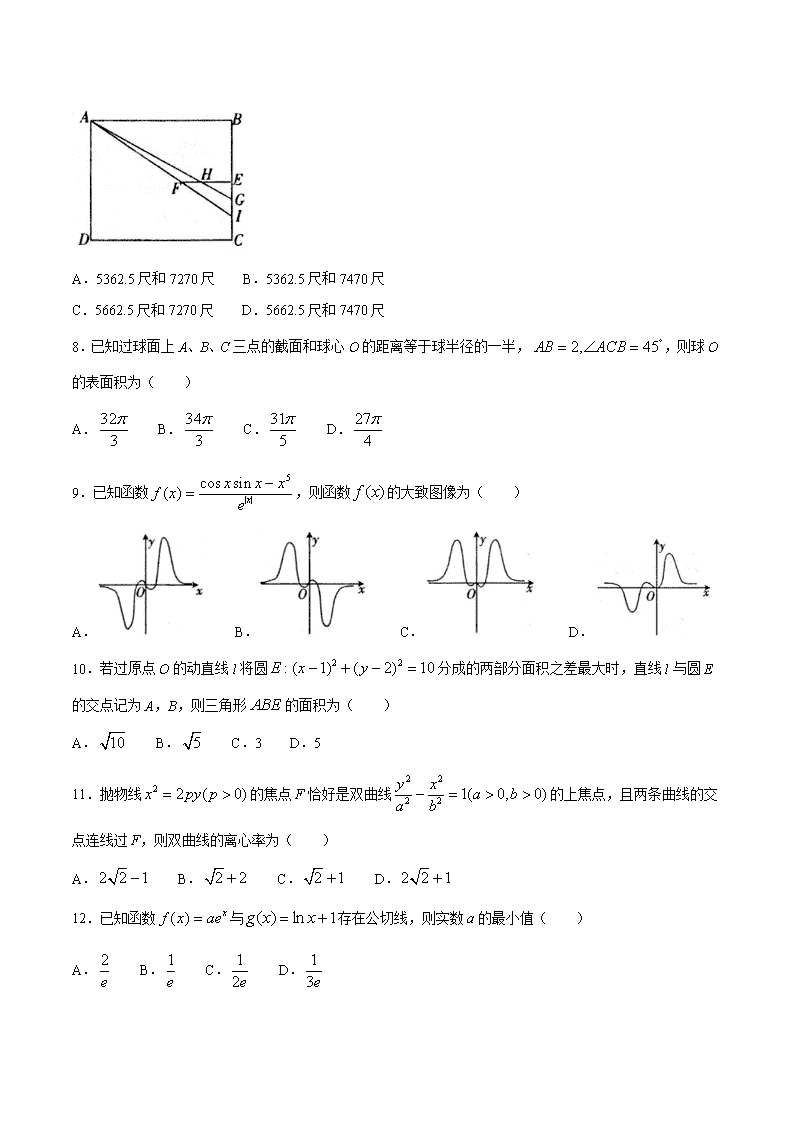7．《海岛算经》第 3 题：今有南望方邑，不知大小．立两表东、西去六丈，齐人目，以索连之．令东表与 邑东南隅及东北隅参相直．当东表之北却行五步，遥望邑西北隅，入索东端二丈二尺六寸半．又却北行去 表一十三步二尺，遥望邑西北隅，适与西表相参合．问邑方及邑去表各几何？答曰：邑方三里四十三步、 四分步之三；邑去表四里四十五步．译文如下：现在要测量南边的一个长方形城市 ABCD ，不知道大小．在 东西两个方向上树立两个标杆 E 和 F， EF 相距 6 丈，标杆和人眼一样高，用绳索连接．令东边的标杆 E 和城市的东南角 C 和东北角 B 平齐．面向标杆 E 退 5 步到达 G 处，从 G 处向城市西北角 A 看，视线交绳 索 EF 于距离东端的标杆 E2 丈 2 尺 6.5 寸的 H 处．从 G 处再退到距离标杆 E13 步 2 尺的 I 处，再向城市西 北角 A 望去，刚好和西边的标杆 F 重合．问城市的长 AB 和 BE 有多远？（1 丈=10 尺，1 步=6 尺，1 尺=10 寸） A．5362.5 尺和 7270 尺 B．5362.5 尺和 7470 尺 C．5662.5 尺和 7270 尺 D．5662.5 尺和 7470 尺 8．已知过球面上 A、B、C 三点的截面和球心 O 的距离等于球半径的一半， 2, 45AB ACB    ，则球 O 的表面积为（ ） A． 32 3  B． 34 3  C． 31 5  D． 27 4  9．已知函数 5 | | cos sin( ) x x x xf x e  ，则函数 ( )f x 的大致图像为（ ） A． B． C． D． 10．若过原点 O 的动直线 l 将圆 2 2: ( 1) ( 2) 10E x y    分成的两部分面积之差最大时，直线 l 与圆 E 的交点记为 A，B，则三角形 ABE 的面积为（ ） A． 10 B． 5 C．3 D．5 11．抛物线 2 2 ( 0)x py p  的焦点 F 恰好是双曲线 2 2 2 2 1( 0, 0)y x a ba b     的上焦点，且两条曲线的交 点连线过 F，则双曲线的离心率为（ ） A． 2 2 1 B． 2 2 C． 2 1 D． 2 2 1 12．已知函数 ( ) xf x ae 与 ( ) ln 1g x x  存在公切线，则实数 a 的最小值（ ） A． 2 e B． 1 e C． 1 2e D． 1 3e 二、填空题：本题共 4 小题，每小题 5 分，共 20 分． 13．已知 x，y 满足不等式组 2 2 0 2 1 0 0 x y x y x         „ ，则点 ( , )P x y 所在区域的面积等于_________． 14．已知单位向量 AB  与 AC  的夹角为 60°，若 AM AB AC    ，且 AM AC  ，则实数 的值为_____． 15．函数 ( )f x 的导数为 ( )f x ，且 2( ) 2 (0) tanf x x f x x   ，则 (0) (0)f f   ______． 16． na 为公差不为 0 的等差数列，且 1 2 3 , , , nk k k ka a a a 恰为等比数列，其中 1 2 33, 5, 9k k k   ，则 nk 为_______． 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题， 每个试题考生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：共 60 分． 17．（12 分） 已知 ABC 的内角 A、B、C 的对边分别为 a、b、c， 2 13sin sin cos2 2A A A      ． （1）求角 A 的大小； （2）若 ABC 的外接圆半径为 1，求 b c 的最大值． 18．（12 分）为研制新冠肺炎的疫苗，某生物制品研究所将所研制的某型号疫苗用在小白鼠身上进行科研和 临床试验，得到如下统计数据： 未感染病毒 感染病毒 总计 未注射疫苗 40 p x 注射疫苗 60 q y 总计 100 100 200 现从未注射疫苗的小白鼠中任取 1 只，取到“感染病毒”的小白鼠的概率为 2 3 ． （1）能否有 99.5%的把握认为注射此疫苗有效？ （2）在未感染病毒的小白鼠中，按木注射疫苗和注射疫苗的比例抽取 5 只进行病理分析，然后从这 5 只小 白鼠中随机抽取 3 只对注射疫苗的情况进行核实，求恰有 1 只为未注射过疫苗的概率． 附：下面的临界值表仅供参考．  2 0P K k… 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 参考公式： 2 2 ( ) ,( )( )( )( ) n ad bcK n a b c da b c d a c b d         ． 19．（12 分）已知圆锥 SO 的侧面展开图为如图所示的半径为 3，圆心角为 2 3  的扇形，扇形中 6ASC   ．圆 锥 SO 中，E 为线段 SC 上一点，且 1 8 EC SE  ． （1）求证： SC  平面OAE ； （2）求点 O 到平面 SEA 的距离． 20．（12 分）已知函数  2 2( ) 2 ln 3f x x ax x x ax    ． （1）求函数 ( )f x 的单调递增区间； （2）若 ( )f x 极大值大于 2，求 a 的取值范围． 21．（12 分）抛物线 2 2 ( 0)y px p  的焦点为 F，准线为 l，点 P 为抛物线上一点， PA l ，垂足为 A， 若直线 AF 的斜率为 3 ，且| | 4PF  ． （1）求抛物线 C 的方程； （2）若过 F 的直线与曲线 C 交于 P，Q 两点，直线 ,OP OQ 与直线 1x  分别交于 A，B 两点，试判断以 AB 为直径的圆是否经过定点？若是，求出定点坐标；若不是，请说明理由． （二）选考题：共 10 分．请考生在第 22、23 题中任选一题作答．如果多做，则按所做的第 一题计分． 22．[选修 4—4：坐标系与参数方程]（10 分） 在平面直角坐标系 xOy 中，已知曲线 3cos: sin x aC y a    （a 为参数），在以原点 O 为极点，x 轴的非负半轴 为极轴建立的极坐标系中，直线 l 的极坐标方程为 2 cos 22 4        ． （1）求曲线 C 的普通方程和直线 l 的直角坐标方程； （2）过曲线 C 上任意一点 P 作与 l 夹角为 60°的直线 m，直线 m 与直线 l 交于点 A，求| |PA 的取值范围． 23．[选修 4—5：不等式选讲]（10 分） （1）设函数 ( ) | 2 | | |f x x x a    ，若关于 x 的不等式 ( ) 3f x … 在 R 上恒成立，求实数 a 的取值范围； （2）已知正数 x，y，z 满足 2 3 1x y z   ，求 3 2 1 x y z   的最小值． “皖南八校”2021 届高三第二次联考·数学（文科） 参考答案、解析及评分细则 1．B ∵ 1 1, , [0,1]2 2A B      ，∴ 1 ,12A B       故选 B． 2．A ∵ 23z i i  ，∴ 3z i   ．∴z 的虚部为 1，故选择 A． 3．D ∵ 02a  ，∴ 1a  ，∵ 2 2 1log log 13  ，∴ 0b  ，∴ 3 3 3log 1 log 2 log 3  ，∴ 0 1c  ．∴ a c b  ．故选择 D． 4．B ∵ na 为等差数列， 1 2 3 21a a a   ，∴ 23 21a  ，∴ 2 7a  ．∵ 3 4 5 45a a a   ，∴ 43 45a  ， ∴ 4 2 4 15, 44 2 a aa d    ，∴ 1 2 3a a d   ．故选择 B． 5．B 第一次循环： 0 1 1, 2 0 1 1k S       ；第二次循环： 1 1 2, 2 1 2 4k S       ；第三次 循环： 2 1 3, 2 4 3 11k S       ；第四次循环： 3 1 4, 2 11 4 26k S       ；第五次循环： 4 1 5, 2 26 5 57k S       ；第六次循环： 5 1 6, 2 57 6 120k S       ，满足条件则输出 S 的 值，而此时 6k  ，因此判断框内应填入的条件是 5k  ．故选 B． 6．D 设阴影部分的面积为 S，结合几何概型公式可得： 4 51 32 22 2 S     ，解得 4 3 5S  ．故选：D． 7．D 依据题意| | 60EF  尺，| | 30EG  尺，| | 22.65EH  尺，| | 80EI  尺， 易知 | | | | | | | |,| | | | | | | | BG EG BI EI AB HE AB EF   ． 设 ,BE x AB y  ，则 30 30 22.65 x y   ① 80 80 60 x y   ② 得 7470, 5662.5x y  故选：D ． 8．A 如图所示 1O ，O 分别为的三角形 ABC 外接圆圆心和球的球心，设三角形 ABC 外接圆半径和球的球 的半径分别为 r，R，由正弦定理 2 2 2sin ABr ACB   ，∴ 2r  ，由图可知 2 2 2 2 RR r     ，∴ 2 8 3R  ， ∴球的表面积 2 324 3S R   ． 9．B 5 | | cos sin( ) ( )x x x xf x f xe      ，得函数 ( )f x 为奇函数，可排除 C 选项；且 5 | |6 cos sin6 6 6 06f e                ， 5 | | cos sin( ) 0f e      ，只有 B 选项符合条件． 10．D 动直线 l 将圆 E 分成的两部分面积之差最大，即过原点的弦最短，弦心距最大，则 l OE 此时 2| | 2 10 2 5AB OE   ，则 1 1| || | 2 5 5 52 2ABES AB OE     ，故选 D． 11．C 设抛物线与双曲线的两个交点分别为 A，B．将 y c 代入 2 2 2 2 1y x a b   得 22| | bAB a  将 y c 代入 2 2 ( 0)x py p  得| | 2AB p ，∴ 22 2b pa  即 2b pa  由两曲线共焦点，∴ 2 p c ，∴ 2 2b ca  ．∴ 2 2 2 0c a ca   ．∴ 2 2 1 0e e   ．∴ 1 2e   ，故选 C． 12．B 设 ( ) xf x ae 和 ( ) ln 1g x x  的切点分别为  , ,( ,ln 1)mm ae n n  ，则 ( )f x 和 ( )g x 切线方程分 别为 1( ), (ln 1) ( )m my ae ae x m y n x nn        ， 即 1( 1) , ln , ( )m my ae x m ae y x n f xn       与 ( )g x 存在公切线，则方程 1 ( 1) ln m m ae n m ae n       有解，即 ln ( 1)ln 1, ( ) ( 1)ln 1a n n h x x x      ， 1( ) ln 1, ( )h x x h xx     在 (0,1) 上递减，在 (1, ) 递增， ( )h x 在 1x  处取到最小值，∴ ln a 的最小值 为 1 ，即 a 的最小值为 1 e ．故选 B． 13． 5 4 作出不等式表示的平面区域，如图 ABC 内部（含边界），由边界的三条直线方程可得 10, , (1,0), (0,2)2A B C    ， ∴ 1 5 512 2 4ABCS     ． 故答案为： 5 4 ． 14． 2 ∵ AM AC  ，∴ 0AM AC   ．∵ AM AB AC    ，∴ ( ) 0AB AC AC      ，即 2 0AB AC AC      ，∴ 11 1 1 02       ，∴ 2   ． 15． 1 ∵ 2( ) 2 (0) tanf x x f x x   ，∴ 2 1( ) 2 2 (0) cosf x x f x     ，∴ (0) 2 (0) 1f f   ，∴ (0) 1f    ， (0) 0f  ，∴ (0) (0) 1f f    ． 16． 2 1n  设数列 nka 为 nb 则 1 3 2 5 3 9, ,b a b a b a   ，∵ 2 5 3 9a a a ，∴     2 1 1 14 2 8a d a d a d    即 1 0a d  ，∴ 0d  ，∴ 1 0a  ，∴ ( 1)na n d  ，设 nb 的公比为 q， 则 5 1 3 3 42 , 22 a db a d q a d      ，∴ 2n n k na b d  即  1 2n nk d d  ，∴ 2 1n nk   ． 17．解：（1）因为 2 13sin sin cos2 2A A A      ， 1 分 所以 23 2cos 1 cos2sin2 12 2 2 A AA    ，即 sin 2 16A      ， 3 分 因为 (0, )A  ，所以 112 ,6 6 6A         ，所以 2 ,6 2 3A A     ． 5 分 （2）因为 ABC 的外接圆半径为 1，所以 32sin 2 32a A    ， 7 分 则 2 2 2 2 2 2 2 2 3( )2 cos ( ) 3 ( ) 4 b ca b c bc A b c bc b c bc b c           … ， 9 分 即 2( )3 4 b c … ，当且仅当 3b c  时取等号， 11 分 故 2 3,b c b c „ 的最大值为 2 3 ． 12 分 18．解：（1）依题意，由 2 40 3 p p  ，得 80p  ， 所以 20, 120, 80q x y   ． 2 分 所以， 2 2 列联表如下表所示： 未感染病毒 感染病毒 总计 未注射疫苗 40 80 120 注射疫苗 60 20 80 总计 100 100 200 由 2 2 200 (40 20 60 80) 33.3 7.879100 100 120 80K         ， 所以有 99.5%的把握认为注射此疫苗有效； 5 分 （2）设“恰有 1 只为未注射过疫苗”为事件 A， 由于在未感染病毒的小白鼠中，按未注射疫苗和注射疫苗的比例 40 2 60 3  抽取， 故抽取的 5 只小白鼠中有 2 只未注射疫苗，分别用 1、2 来表示，3 只已注射疫苗的小白鼠用 a、b、c 来表 示， 7 分 从这 5 只小白鼠中随机抽取 3 只，可能的情况有：(1,2, )a 、(1,2, )b 、(1,2, )c 、(1, , )a b 、(1, , )a c 、(1, , )b c 、 (2, , )a b 、 (2, , )a c 、 (2, , )b c 、 ( , , )a b c ，共 10 种， 9 分 其中恰有 1 只为未注射过疫苗有： (1, , )a b 、 (1, , )a c 、 (1, , )b c 、 (2, , )a b 、 (2, , )a c 、 (2, , )b c ，共 6 种， 11 分 所以 6 3( ) 10 5P A   ，即恰有 1 只为未注射过疫苗的概率为 3 5 ． 12 分 19．解：圆锥底面半径为 1，高 2 2, 1 36OAC     ，∴ 2OAC   ，∴OA OC ． 又∵OS OA ，∴OS OC O  ，∴OA  平面 SOC ，又∴ SC  平面 SOC ，∴ SC OA ． ∵OS OA ，且∴OA OC ，∴OA OC ． 2 分 ∵ 1 9 EC SC  ，∴ 1 3EC  ，∴ 2EC SC OC  ，∴ OC EC SC OC  ． ∴ OEC SOC ∽ ，∴ SC OE ． 4 分 又∵OE OA O  ，∴ SC  平面OAE ． 5 分 （2）因为 SE 是三棱锥 S AOE 的高，所以 SC AE ， 在 Rt SAE 中可求得此时 8 17,3 3SE AE  ． 7 分 由已知可得，∵OE SC SO OC   ，∴ 2 2 1 2 2 3 3 SO OCOE SC     ， 8 分 ∵ 1 1, 3 3S OAE O SAE OAE SAEV V S SE S h       ． ∴ 1 1 1 1 3 2 3 2OA OE SE SE AE h             ． ∴ 2 34 17 OA OEh AE   ． 12 分 20．解： 1( ) 2( )ln 2 2 3 2( ) ln 2f x x a x x a x a x a x             ． 1 分 （1） 0a„ 时( , )e  单增， ( )f x 的单调递增区间为 ( , )e  ； 0 a e  时， ( )f x 在 (0, )a 和 ( , )e  单增， ( )f x 的单调递增区间为 (0, )a 和 ( , )e  ； a e 时， ( )f x 在 (0, ) 单增， ( )f x 的单调递增区间为 (0, ) ； a e 时， ( )f x 在 (0, )e 和 ( , )a  单增， ( )f x 的单调递增区间为 (0, )e 和 ( , )a  ． 5 分 （2）由（1）， 0a„ 和 a e 时，无极大值，不成立． 7 分 当 a e 时，极大值 ( ) 2 22 ef e a e   ，解得 1 4 ea e   ， 由于 1 1 3 1 31 04 4 4 e e ee e e e           ，所以 a e ． 8 分 当 0 a e  时，极大值 2( ) (2 ln ) 2f a a a   ，得 2 22 lna a   ，令 2t a ，则 1 2( ) 2 ln2g t t t    ． 2 2 1 2 4( ) , ( )2 2 tg t g tt t t      在 4t  取得极大值 (4) 0g  ，且 (1) 0g  ． 而 ,a e t e  ，而 ( )g t 在 (1, )e 单增，所以 ( ) 0g t  解为 (1, )e ，则 (1, )a e ． 11 分 综上 (1, ) ( , )a e e   ． 12 分 21．解：（1）∵直线 AF 的斜率为 3 ，∴直线 AF 的方程为 3 2 py x      ，当 2 px   时， 3y p 可得 A 点坐标为 , 32 p p    ． ∵ PA l ，A 为垂足，∴P 点纵坐标为 3p ，∵| | 4PF  ，∴P 点横坐标为 4 2 p ，∴P 点坐标 4 , 32 p p    为代入抛物线方程得∴ 23 2 4 2 pp p     ，∴ 2p  ．故抛物线 C 的方程为 2 4y x ． 5 分 （2）设直线 PQ 的方程为    1 1 2 21, , , ,x my P x y Q x y  ， 联立 2 4 1 y x x my      ， 整理得： 2 2 1 2 1 24 4 0, 16 16 0, 4 , 4y my m y y m y y           ， 7 分 直线OP 的方程为 1 1 1 4yy x xx y   ， 同理：直线OQ 的方程为 2 4y xy  ， 令 1x  得， 1 2 4 41, , 1,A By y            ， 设 AB 中点 T 的坐标为  ,T Tx y ， 则  1 21 2 1 2 4 4 21, 22T T y yy yx y my y       ， 所以 (1, 2 )T m ． 9 分  2 1 2 1 2 22 1 1 2 1 2 4 444 4| | 16 164 y y y yy yAB my y y y        ． 圆的半径为 216 16 2 mr  ．所以以 AB 为直径的圆的方程为 2 2 2( 1) ( 2 ) 4 4x y m m     ． 展开可得 2 2( 1) 4 4x y my    ，令 0y  ，可得 2( 1) 4x   ，解得 3x  或 1x   ． 从而以 AB 为直径的圆经过定点 ( 1,0) 和 (3,0)． 12 分 22．解：（1）曲线 C 化为普通方程为： 2 2 13 x y  ． 2 分 由 2 cos 22 4        ，得 cos sin 4      ， 所以直线 l 的直角坐标方程为 4 0x y   ． 4 分 （2）设点 P 到直线 l 的距离为 d， ( 3cos ,sin )P   ，∴ | 3cos sin 4 | 2 d    ． ∴ 6 | 3cos sin 4 || | sin60 3 dPA       ． ∴ 6 2sin 43| | 3PA      ． 8 分 ∴ 2 6| | ,2 63PA      ． 10 分 23．解：（1） ( ) | 2 | | | | 2 | | 2 |f x x x a x x a a        … ． 原命题等价于 min( ) 3,| 2 | 3f x a … … ，∴ 5a „ 或 1a… ． 5 分 （2）由于 , , 0x y z  ，所以 3 2 1 3 2 1 3 2( 2 3 ) 2 3x y z x y zx y z x y z x y             … 2 21 ( 3 2 3) 16 8 3z        ． 当且仅当 2 32 3 1 y x z y x z   ，即 : : 3: 3 :1x y z  时，等号成立． 3 2 1 x y z   的最小值为16 8 3 ． 10 分