安徽省颍上一中2013-2014学年高一数学上学期期中试题新人教A版 7页

颍上一中2013~2014学年度高一上学期期中试题数学 ‎（时间：120分钟 满分：150分）‎ 一、选择题（本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一个是符合题目要求的）‎ ‎1．如图所示的韦恩图中，集合，集合，则图中阴影部分所表示的集合为(　　)‎ A． B． C． D．‎ ‎2. 下列函数中,在区间上是增函数的是（ ）‎ A． B． C． D．‎ ‎3. 下列各个图形中，不可能是函数的图像的是( )‎ ‎4. 设函数，则的表达式是（ ）‎ A． B． C． D．‎ ‎5.设，，，则的大小关系是（ ）‎ A． B． C． D． ‎ ‎（4）‎ ‎（3）‎ ‎（1）‎ 俯视图 俯视图 俯视图 侧视图 侧视图 侧视图 侧视图 正视图 正视图 正视图 正视图 ‎（2）‎ 俯视图 ‎6. 如图⑴、⑵、⑶、⑷为四个几何体的三视图，根据三视图可以判断这四个几何体依次为（ ）‎ ‎ ‎ A．三棱台、三棱柱、圆锥、圆台 B．三棱台、三棱锥、圆锥、圆台 ‎ ‎ C．三棱柱、四棱锥、圆锥、圆台 D．三棱柱、三棱台、圆锥、圆台 ‎7. 如果函数在区间(－∞，4]上是减函数，那么实数a的取值范围是（ ） ‎ ‎ A．a≥9 B．a≤－‎3 C．a≥5 D．a≤－7‎ ‎8. 已知函数的图像是连续不断的，且有如下的对应值表：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎－5‎ ‎2‎ ‎8‎ ‎12‎ ‎－5‎ ‎－10‎ ‎ 则函数上的零点个数至少为（ ）‎ ‎ A．1个 B．2个 C．3个 D．4个 ‎9.下列推理中，错误的个数为 （ ）‎ ‎①、若直线上有两点A、B在平面内，则直线必为内直线；‎ ‎②、若为两个不同平面，A、B为的两个公共点，则一定还有其他公共点，这些公共点都在直线AB上；‎ ‎③、若直线在平面外，点A为上一点，则点A一定也在平面外； ‎ ‎④、若平面有三个不共线的公共点A、B、C，则一定重合.‎ A．0个 B．1个 C．2个 D．3个 ‎10. 若函数的定义域为，它在定义域内既是奇函数又是增函数，且 ,则实数的取值范围是( )‎ A． B． C． D． ‎ 二、填空题（本大题共5小题，每小题5分，共25分．把答案填在答题卷的相应位置）‎ ‎11. 设函数=，则=________‎ ‎12. 已知正三角形ABC的边长为a，那么在斜二测画法下△ABC的平面直观图△A1B‎1C1的面积为 ‎ ‎13. 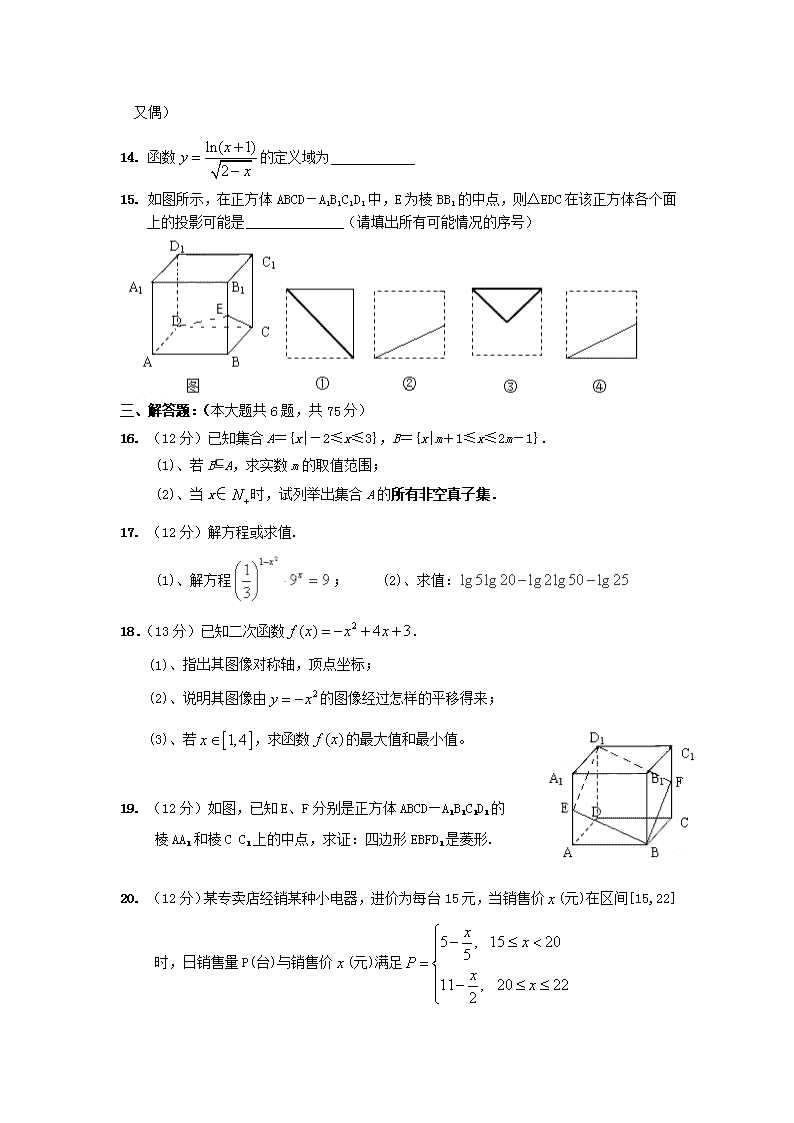19世纪德国数学家狄利克雷（1805—1859）定义了一个“奇怪的函数”——狄利克雷函数：，则该函数为 ‎ ‎ 函数（选填：奇、偶、非奇非偶、既奇又偶）‎ ‎14. 函数的定义域为 ‎ ‎15. 如图所示，在正方体ABCD－A1B‎1C1D1中，E为棱BB1的中点，则△EDC在该正方体各个面上的投影可能是 （请填出所有可能情况的序号）‎ 三、解答题：（本大题共6题，共75分）‎ ‎16. （12分）已知集合A＝{x|－2≤x≤3}，B＝{x|m＋1≤x≤‎2m－1}．‎ ‎(1)、若B⊆A，求实数m的取值范围；‎ ‎(2)、当x∈时，试列举出集合A的所有非空真子集．‎ ‎17. （12分）解方程或求值.‎ ‎(1)、解方程； (2)、求值：‎ ‎18．（13分）已知二次函数.‎ ‎(1)、指出其图像对称轴，顶点坐标；‎ ‎(2)、说明其图像由的图像经过怎样的平移得来；‎ ‎(3)、若，求函数的最大值和最小值。‎ ‎19. （12分）如图，已知E、F分别是正方体ABCD—A1B‎1C1D1的 棱AA1和棱C C1上的中点，求证：四边形EBFD1是菱形.‎ ‎20. （12分）某专卖店经销某种小电器，进价为每台15元，当销售价(元)在区间[15,22]时，日销售量P(台)与销售价(元)满足 ‎ ‎ (1)、当定价为每台18元时，该专卖店的日销售利润为多少?‎ ‎ (2)、请列出该店经销这种小电器的日销售利润y与销售价的关系式，并求销售价为多少元时，专卖店的日利润最高? ‎ ‎21.（14分） 已知为定义在[－1，1]上的奇函数，且当时，.‎ ‎（1）、试用函数单调性定义证明：在上是减函数； ‎ ‎（2）、求函数在[－1，1]上的解析式；‎ ‎（3）、要使方程在区间[－1，1]上恒有实数解，求实数b的取值范围.‎ 颍上一中2013~2014年度高一上学期期中试题答案 数 学 一、选择题 ‎1—5 CAABD 6—10 CABBD 二、填空题 ‎11、 12、 13、偶 14、 15、①②④‎ 三、解答题 ‎16、解：（1）、由B⊆A，知当时，m＋1>‎2m－1，得m<2； ………………2分 ‎ 当时，，得m=2. ………………5分 ‎ 综上所述，m≤2即为所求范围。 ………………7分 ‎ （2）、由x∈，则A＝{x|－2≤x≤3}={1,2,3}，其非空真子集罗列如下：‎ ‎ {1}，{2}，{3}，{1,2}，{1,3}，{2,3}。 ………………12分 ‎（多一个或少一个均扣2分，扣完为止）‎ ‎17、解：（1）、由题意知 原方程可化为，从而有，‎ 即， ………………4分 ‎ 解得 ………………6分 ‎（2）、原式=lg5（lg2+1）—lg2（lg5+1）-2lg5 ………………9分 ‎ = -lg5 -lg2‎ ‎ = - 1 ………………12分 ‎18、解：（1）、由题意知：二次函数的对称轴方程为x=2，顶点坐标为（2,7）；………4分 ‎（2）、二次函数图像可由的图像先向右平移2个单位，再向上平移7个单位得到； ………………8分 ‎（3）、由（1）知，在区间[1,2]上递增，在[2,4]递减，所以 ‎ 当x=2时，； ………………10分 ‎ 当x=4时， ………………13分 ‎(或者：由对称轴x=2在区间[1,4]内，且图像开口向下，所以可知当x=2时，；当x=4时，。酌情给分)‎ ‎19、证明：取棱BB1中点为G，连C‎1G、EG， ………………2分 由正方体性质，侧面AB B‎1A1为正方形，又E、G分别为边AA1、BB1中点，‎ 所以 ‎ 从而四边形为平行四边形， ………………5分 又F、G分别为棱CC1、BB1中点，由侧面CB B‎1C1为正方形，知 ‎ 四边形为平行四边形，所以, ………………8分 又，由平行公理可知，从而四边形为平行四边形.………10分 由ABCD—A1B‎1C1D1为正方体，不妨设其棱长为a，易知 而由四边形为平行四边形，从而即为菱形。………………12分 ‎(不在图上标出辅助线或辅助线用虚线的请另扣2分)‎ ‎20、解：（1）、4.2元 ……………………3分 ‎ （2）、由题意，‎ ‎ ……………………7分 当时，知；当时，，此时。……………10分 综上，销售价为20元时，专卖店的日利润最高。 ……………12分 ‎（若当时“”被写成“”可不扣分）‎ ‎21、解及证：‎ ‎（1）、对于任意且，有 …………1分 ‎ ………3分 ‎ ∵，∴，，‎ ‎ 又函数在R内递增，所以，由此 ‎ ，即 …………4分 ‎ ∴在上是减函数； …………5分 ‎（2）、由题意为定义在[－1，1]上的奇函数，且当时，.‎ ‎ 所以有， …………7分 当时，有； …………9分 综上：函数在[－1，1]上的解析式为 ‎ ； …………10分 ‎（3）、方程可化为，记，‎ 由(1)及题设，在[－1，1]为奇函数，且在上是减函数，‎ ‎ ∴当时，，…12分 ‎ 由奇函数性质，当时，， ……13分 综上，值域为， ‎ 所以当图像与直线有公共点时，b的范围为，‎ 也即方程在[－1，1]上恒有实数解时实数b的取值范围为。……14分 ‎ （用函数图像与直线y=x+b相交求b的范围的，请酌情给分） ‎