2021高考数学新高考版一轮习题：专题7 第60练 高考大题突破练——立体几何与 空间向量 Word版含解析 6页

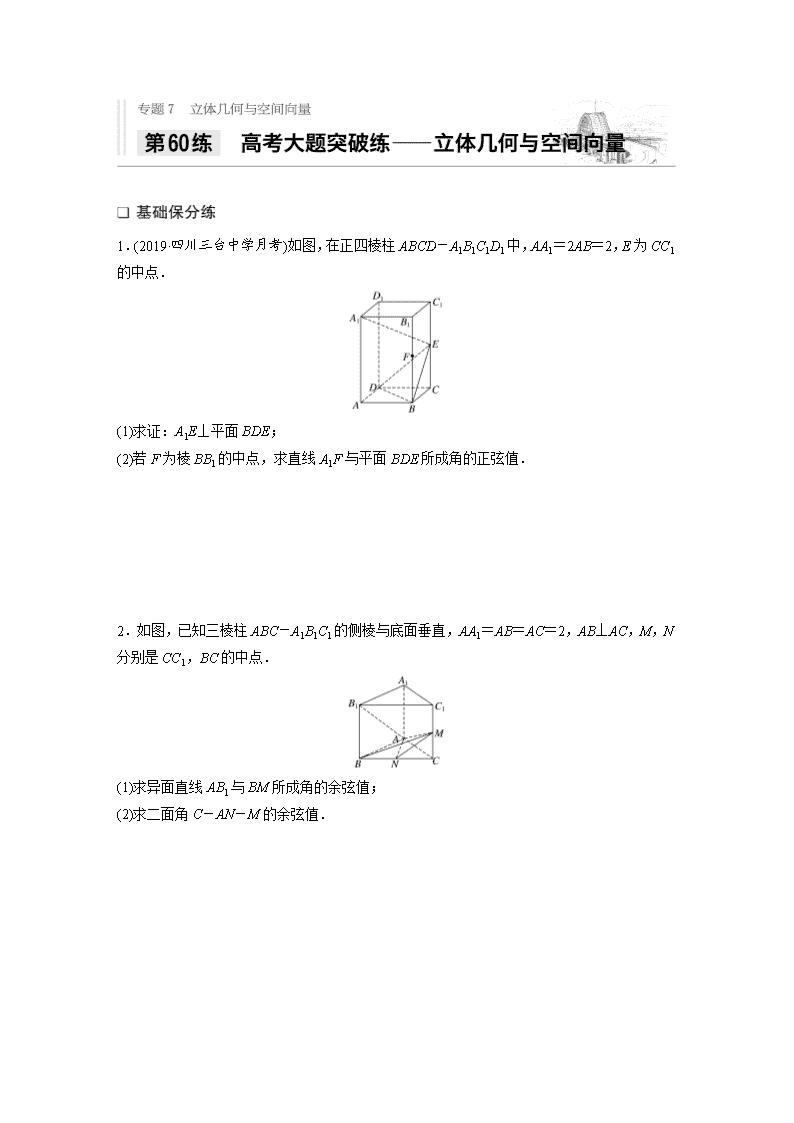
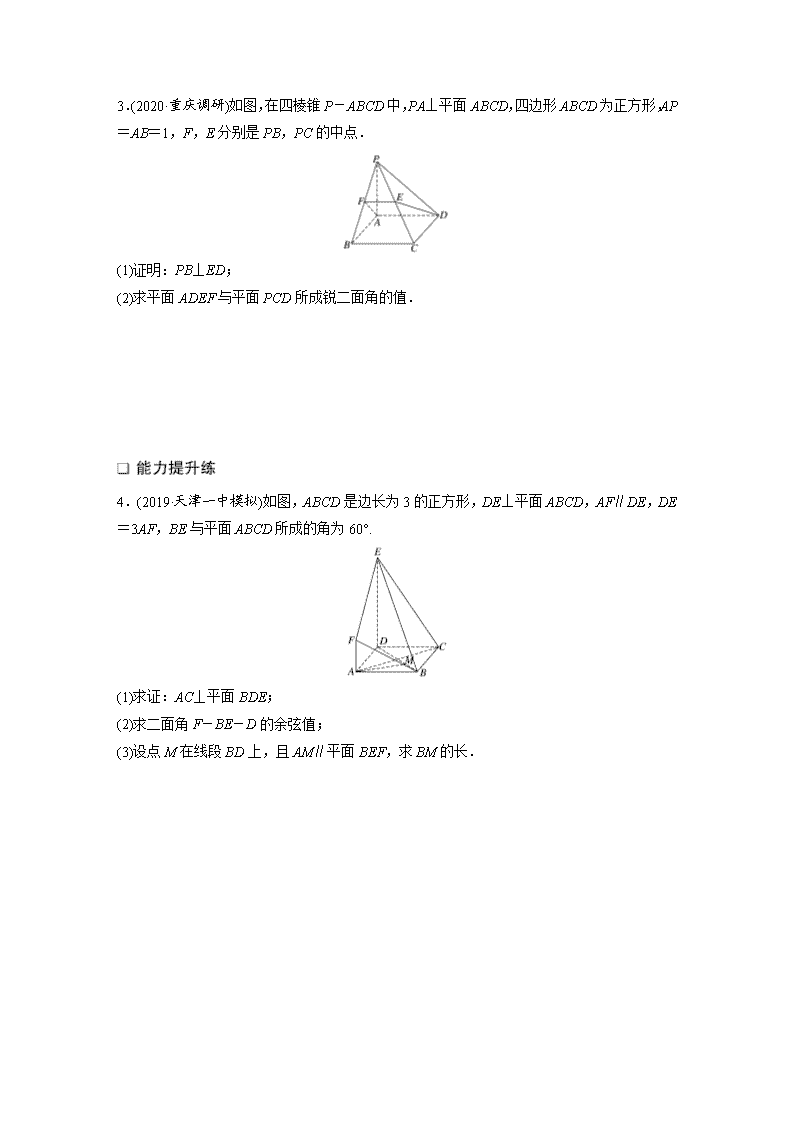
‎1．(2019·四川三台中学月考)如图，在正四棱柱ABCD－A1B1C1D1中，AA1＝2AB＝2，E为CC1的中点．‎ ‎(1)求证：A1E⊥平面BDE；‎ ‎(2)若F为棱BB1的中点，求直线A1F与平面BDE所成角的正弦值．‎ ‎2．如图，已知三棱柱ABC－A1B1C1的侧棱与底面垂直，AA1＝AB＝AC＝2，AB⊥AC，M，N分别是CC1，BC的中点．‎ ‎(1)求异面直线AB1与BM所成角的余弦值；‎ ‎(2)求二面角C－AN－M的余弦值．‎ ‎3．(2020·重庆调研)如图，在四棱锥P－ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，AP＝AB＝1，F，E分别是PB，PC的中点．‎ ‎(1)证明：PB⊥ED；‎ ‎(2)求平面ADEF与平面PCD所成锐二面角的值．‎ ‎4．(2019·天津一中模拟)如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE＝3AF，BE与平面ABCD所成的角为60°.‎ ‎(1)求证：AC⊥平面BDE；‎ ‎(2)求二面角F－BE－D的余弦值；‎ ‎(3)设点M在线段BD上，且AM∥平面BEF，求BM的长．‎ 答案精析 ‎1．(1)证明　以D为坐标原点，DA所在直线为x轴，DC所在直线为y轴，DD1所在直线为z轴，建立如图所示的空间直角坐标系．‎ 则有B(1,1,0)，E(0,1,1)，A1(1,0,2)，C1(0,1,2)，‎ ‎∴＝(－1,1，－1)，＝(1,1,0)，＝(0,1,1)，＝(0,0,1)，‎ ‎∵·＝0，·＝0，‎ ‎∴⊥，⊥，‎ 又∵DB∩DE＝D，DB，DE⊂平面BDE，‎ ‎∴A1E⊥平面BDE.‎ ‎(2)解　由(1)知，平面BDE的法向量为＝(－1,1，－1)，‎ 易知F(1,1,1)，＝(0,1，－1)，‎ 设直线A1F与平面BDE所成的角为θ，‎ 则sin θ＝|cos〈，〉|＝＝.‎ 故直线A1F与平面BDE所成角的正弦值为.‎ ‎2．解　(1)如图，以A为坐标原点，AB，AC，AA1所在直线分别为x，y，z轴建立空间直角坐标系，则B1(2,0,2)，B(2,0,0)，M(0,2,1)，N(1,1,0)，‎ ‎∴＝(2,0,2)，＝(－2,2,1)．‎ ‎∴cos〈，〉＝＝＝－，‎ ‎∴异面直线AB1与BM所成角的余弦值为.‎ ‎(2)平面ANC的一个法向量为n＝(0,0,1)．‎ 设平面AMN的一个法向量为m＝(x，y，z)．‎ ‎∵＝(0,2,1)，＝(1,1,0)，‎ 由m·＝0，m·＝0得，‎ 不妨取x＝1，则y＝－1，z＝2，‎ ‎∴m＝(1，－1,2)，‎ ‎∴cos〈m，n〉＝＝＝，‎ ‎∴二面角C－AN－M的余弦值为.‎ ‎3．(1)证明　∵PA⊥平面ABCD，∴PA⊥AD，‎ 又AD⊥AB，AB，PA⊂平面PAB，PA∩AB＝A，‎ ‎∴AD⊥平面PAB，∴AD⊥PB，‎ 而等腰三角形PAB中有PB⊥AF，AD，AF⊂平面ADEF，AD∩AF＝A，∴PB⊥平面ADEF，‎ 而ED⊂平面ADEF，∴PB⊥ED.‎ ‎(2)解　易知AB，AD，AP两两垂直，‎ 故分别以其所在直线为坐标轴建立空间直角坐标系A－xyz如图所示，‎ 则A(0,0,0)，P(0,0,1)，B(1,0,0)，C(1，1,0)，D(0,1,0)，‎ 求得平面ADEF的一个法向量为m＝(1,0，－1)，‎ 平面PCD的一个法向量为n＝(0,1,1)，‎ ‎∴cos〈m，n〉＝－，‎ ‎∴平面ADEF与平面PCD所成锐二面角为60°.‎ ‎4．(1)证明　因为DE⊥平面ABCD，所以DE⊥AC，‎ 因为ABCD是正方形，所以AC⊥BD，‎ 又BD∩DE＝D，BD，DE⊂平面BDE，‎ 从而AC⊥平面BDE.‎ ‎(2)解　因为DA，DC，DE两两垂直，分别以其所在直线为坐标轴建立空间直角坐标系D－xyz如图所示．‎ 因为BE与平面ABCD所成的角为60°，即∠DBE＝60°，‎ 所以＝.‎ 由AD＝3，DB＝3可知DE＝3，AF＝，‎ 则A(3,0,0)，F(3,0，)，E(0,0,3)，‎ B(3,3,0)，C(0,3,0)，‎ 所以＝(0，－3，)，＝(3,0，－2)，‎ 设平面BEF的法向量为n＝(x，y，z)，‎ 则即 令z＝，则n＝(4,2，)，‎ 因为AC⊥平面BDE，所以为平面BDE的法向量，‎ ＝(3，－3,0)，‎ 所以cos〈n，〉＝ ‎＝＝.‎ 因为二面角为锐角，‎ 所以二面角F－BE－D的余弦值为.‎ ‎(3)解　点M是线段BD上一个动点，‎ 设M(t，t,0)，则＝(t－3，t,0)(0≤t≤3)，‎ 因为AM∥平面BEF，所以·n＝0，‎ 即4(t－3)＋2t＝0，解得t＝2.‎ 此时，点M坐标为(2,2,0)，BM＝BD＝，符合题意．‎