2014年高考数学（文科）真题分类汇编L单元　算法初步与复数 11页

‎ 数 学 L单元　算法初步与复数 ‎ L1　算法与程序框图 ‎4．L1[2014·安徽卷] 如图11所示，程序框图(算法流程图)的输出结果是(　　)‎ 图11‎ A．34 B．‎55 C．78 D．89‎ ‎4．B　[解析] 由程序框图可知，列出每次循环过后变量的取值情况如下：‎ 第一次循环，x＝1，y＝1，z＝2；‎ 第二次循环，x＝1，y＝2，z＝3；‎ 第三次循环，x＝2，y＝3，z＝5；‎ 第四次循环，x＝3，y＝5，z＝8；‎ 第五次循环，x＝5，y＝8，z＝13；‎ 第六次循环，x＝8，y＝13，z＝21；‎ 第七次循环，x＝13，y＝21，z＝34；‎ 第八次循环，x＝21，y＝34，z＝55，不满足条件，跳出循环．‎ ‎4．L1[2014·北京卷] 执行如图11所示的程序框图，输出的S值为(　　)‎ 图11‎ A．1 B．3‎ C．7 D．15‎ ‎4．C　[解析] S＝20＋21＋22＝7.‎ ‎14．L1[2014·北京卷] 顾客请一位工艺师把A，B两件玉石原料各制成一件工艺品．工艺师带一位徒弟完成这项任务．每件原料先由徒弟完成粗加工，再由工艺师进行精加工完成制作，两件工艺品都完成后交付顾客．两件原料每道工序所需时间(单位：工作日)如下：‎ 工序时间原料 粗加工 精加工 原料A ‎9‎ ‎15‎ 原料B ‎6‎ ‎21‎ 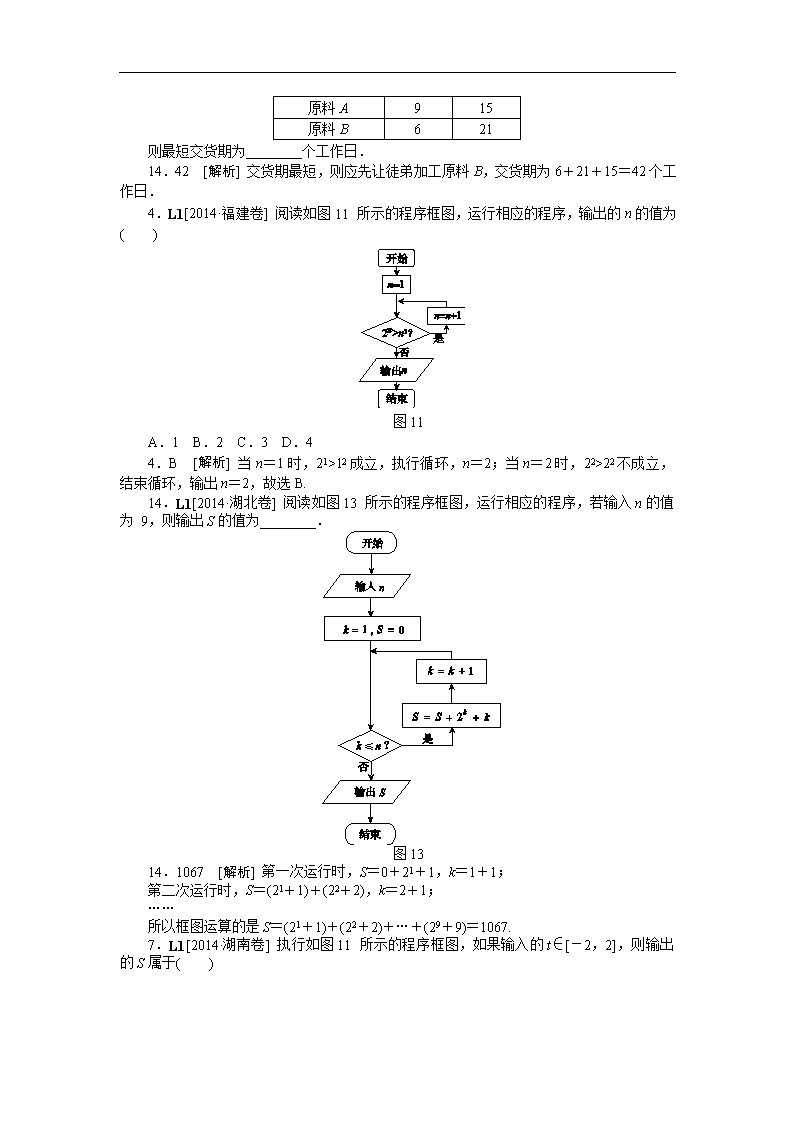则最短交货期为________个工作日．‎ ‎14．42　[解析] 交货期最短，则应先让徒弟加工原料B，交货期为6＋21＋15＝42个工作日．‎ ‎4．L1[2014·福建卷] 阅读如图11所示的程序框图，运行相应的程序，输出的n的值为(　　)‎ 图11‎ A．1 B．‎2 C．3 D．4‎ ‎4．B　[解析] 当n＝1时，21>12成立，执行循环，n＝2；当n＝2时，22>22不成立，结束循环，输出n＝2，故选B.‎ ‎14．L1[2014·湖北卷] 阅读如图13所示的程序框图，运行相应的程序，若输入n的值为 9，则输出S的值为________．‎ 图13‎ ‎14．1067　[解析] 第一次运行时，S＝0＋21＋1，k＝1＋1；‎ 第二次运行时，S＝(21＋1)＋(22＋2)，k＝2＋1；‎ ‎……‎ 所以框图运算的是S＝(21＋1)＋(22＋2)＋…＋(29＋9)＝1067.‎ ‎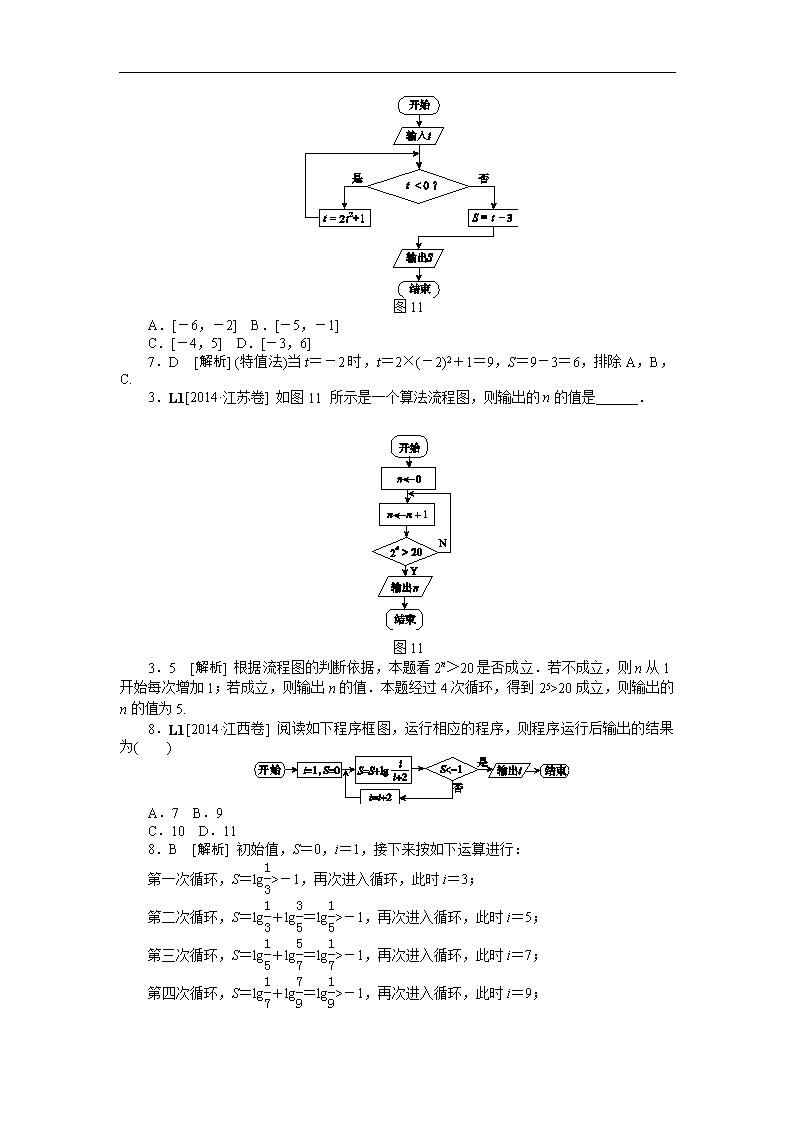7．L1[2014·湖南卷] 执行如图11所示的程序框图，如果输入的t∈[－2，2]，则输出的S属于(　　)‎ 图11‎ A．[－6，－2] B．[－5，－1]‎ C．[－4，5] D．[－3，6]‎ ‎7．D　[解析] (特值法)当t＝－2时，t＝2×(－2)2＋1＝9，S＝9－3＝6，排除A，B，C.‎ ‎3．L1[2014·江苏卷] 如图11所示是一个算法流程图，则输出的n的值是______．‎ 图11‎ ‎3．5　[解析] 根据流程图的判断依据，本题看2n＞20是否成立．若不成立，则n从1开始每次增加1；若成立，则输出n的值．本题经过4次循环，得到25>20成立，则输出的n的值为5.‎ ‎8．L1[2014·江西卷] 阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为(　　)‎ A．7 B．9‎ C．10 D．11‎ ‎8．B　[解析] 初始值，S＝0，i＝1，接下来按如下运算进行：‎ 第一次循环，S＝lg>－1，再次进入循环，此时i＝3；‎ 第二次循环，S＝lg＋lg＝lg>－1，再次进入循环，此时i＝5；‎ 第三次循环，S＝lg＋lg＝lg>－1，再次进入循环，此时i＝7；‎ 第四次循环，S＝lg＋lg＝lg>－1，再次进入循环，此时i＝9；‎ 第五次循环，S＝lg＋lg＝lg<－1，退出循环，此时i＝9.‎ ‎13．L1[2014·辽宁卷] 执行如图13所示的程序框图，若输入n＝3，则输出T＝________．‎ ‎13．20　‎ 图13‎ ‎[解析] 由题意可知，第一步，i＝1，S＝1，T＝1；第二步，i＝2，S＝3，T＝4；第三步，i＝3，S＝6，T＝10；第四步，i＝4，S＝10，T＝20.‎ ‎8．L1[2014·新课标全国卷Ⅱ] 执行如图12所示的程序框图，如果输入的x，t均为2，则输出的S＝(　　)‎ A．4 B．‎5 C．6 D．7‎ 图12‎ ‎8．D　[解析] 当x＝2，t＝2时，依次可得：M＝1，S＝3，k＝1≤2；M＝2，S＝5，k＝2≤2；M＝2，S＝7，k＝3>2，输出S＝7.‎ ‎9．L1[2014·全国新课标卷Ⅰ] 执行如图11的程序框图，若输入的a，b，k分别为1，2，3，则输出的M＝(　　)‎ 图11‎ A. B. C. D. ‎9．D　[解析] 第一次循环后，M＝，a＝2，b＝，n＝2；‎ 第二次循环后，M＝，a＝，b＝，n＝3；‎ 第三次循环后，M＝，a＝，b＝，n＝4，‎ 此时n>k(n＝4，k＝3)，结束循环，输出M＝.‎ ‎11．L1[2014·山东卷] 执行如图13所示的的程序框图，若输入的x的值为1，则输出的n的值为________．‎ 图13‎ ‎11．3　[解析] x＝1满足不等式，执行循环后x＝2，n＝1；x＝2满足不等式，执行循环后得x＝3，n＝2；x＝3满足不等式，执行循环后得x＝4，n＝3.x＝4不满足不等式，结束循环，输出n＝3.‎ ‎4．L1[2014·陕西卷] 根据图11所示的框图，对大于2的整数N，输出的数列的通项公式是(　　)‎ 图11‎ A．an＝2n B．an＝2(n－1)‎ C．an＝2n D．an＝2n－1‎ ‎4．C　[解析] 阅读题中所给的程序框图可知输出的数列为2，2×2＝22，2×22＝23，2×23＝24，…，2×2N－1＝2N，故其通项公式为an＝2n.‎ ‎6．E5、L1[2014·四川卷] 执行如图12的程序框图，如果输入的x，y∈R，那么输出的S的最大值为(　　)‎ 图12‎ A．0 B．‎1 C．2 D．3‎ ‎6．C　[解析] 题中程序输出的是在的条件下S＝2x＋y的最大值与1中较大的数．结合图像可得，当x＝1，y＝0时，S＝2x＋y取最大值2，2>1，故选C.‎ ‎11．L1[2014·天津卷] 阅读图13所示的框图，运行相应的程序，输出S的值为________．‎ ‎11．－4　[解析] 由程序框图易知，S＝(－2)3＋(－2)2＝－4.‎ ‎13．L1[2014·浙江卷] 若某程序框图如图14所示，当输入50时，则该程序运行后输出的结果是________．‎ 图14‎ ‎13．6　[解析] 第一次运行，S＝1，i＝2；第二次运行，S＝4，i＝3；第三次运行，S＝11，i＝4；第四次运行，S＝26，i＝5；第五次运行，S＝57，i＝6，此时S>n，输出i＝6.‎ ‎5．L1[2014·重庆卷] 执行如图11所示的程序框图，则输出s的值为(　　)‎ 图11‎ A．10 B．17‎ C．19 D．36‎ ‎5．C　[解析] 第一次循环结束，得s＝0＋2＝2，k＝2×2－1＝3；第二次循环结束，得s＝2＋3＝5，k＝2×3－1＝5；第三次循环结束，得s＝5＋5＝10，k＝2×5－1＝9；第四次循环结束，得s＝10＋9＝19，k＝2×9－1＝17>10，此时退出循环．故输出s的值为19.‎ L2　基本算法语句 L3　算法案例 L4　复数的基本概念与运算 ‎1．L4[2014·重庆卷] 实部为－2，虚部为1的复数所对应的点位于复平面的(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎1．B　[解析] 由条件知复数在复平面内对应的点为(－2，1)，位于第二象限．‎ ‎1．L4[2014·安徽卷] 设i是虚数单位，复数i3＋＝(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A．－i B．i C．－1 D．1‎ ‎1．D　[解析] i3＋＝－i＋＝1.‎ ‎9．L4[2014·北京卷] 若(x＋i)i＝－1＋2i(x∈R)，则x＝________．‎ ‎9．2　[解析] ∵(x＋i)i＝－1＋xi＝－1＋2i，∴x＝2.‎ ‎2．L4[2014·福建卷] 复数(3＋2i)i等于(　　)‎ A．－2－3i B．－2＋3i ‎ C．2－3i D．2＋3i ‎2．B　[解析] (3＋2i)i＝3i＋2i2＝－2＋3i，故选B.‎ ‎2．L4[2014·广东卷] 已知复数z满足(3－4i)z＝25，则z＝(　　)‎ A．－3－4i B．－3＋4i ‎ C．3－4i D．3＋4i ‎2．D　[解析] ∵(3－4i)z＝25，∴z＝＝＝3＋4i.‎ ‎10．ML、L4[2014·广东卷] 对任意复数ω1，ω2，定义ω1*ω2＝ω1ω2，其中ω2是ω2的共轭复数，对任意复数z1，z2，z3有如下四个命题：‎ ‎①(z1＋z2)*z3＝(z1*z3)＋(z2*z3)；‎ ‎②z1*(z2＋z3)＝(z1*z2)＋(z1*z3)；‎ ‎③(z1*z2)*z3＝z1*(z2*z3)；‎ ‎④z1*z2＝z2*z1.‎ 则真命题的个数是(　　)‎ A．1 B．2 ‎ C．3 D．4‎ ‎10．B　[解析] 根据新定义知，(z1＋z2)*z3＝(z1＋z2)z3＝(z1*z3)＋(z2*z3)，所以①正确；对于②，z1*(z2＋z3)＝z1z2＋z3＝z1z2＋z1z3＝(z1*z2)＋(z1*z3)，所以正确；对于③，左边＝(z1z2)*z3＝z1z2　　z3；‎ 右边＝z1*(z23)＝z1z2　　z3＝z1z2z3＝z1z2，不正确；对于④，可以通过举特殊例子进行判断，z1＝1＋i，z2＝2＋i，左边＝z1*z2＝z1z2＝(1＋i)(2＋i)＝3＋i，右边＝z2*z1＝z2z1＝(2＋i)(1－i)＝3－i，所以④不正确．‎ ‎2．L4[2014·湖北卷] i为虚数单位，＝(　　)‎ A．1 B．－‎1 C．i D．－i ‎2．B　[解析] ＝＝＝－1.故选B.‎ ‎11．L4[2014·湖南卷] 复数(i为虚数单位)的实部等于________．‎ ‎11．－3　[解析] 因为＝＝－3－i，所以实部为－3.‎ ‎2．L4[2014·江苏卷] 已知复数z＝(5－2i)2(i为虚数单位)，则z的实部为________．‎ ‎2．21　[解析] 根据复数的乘法运算公式知，z＝(5－2i)2＝52－2×5×2i＋(2i)2＝21－20i，故实部为21，虚部为－20.‎ ‎1．L4[2014·江西卷] 若复数z满足z(1＋i)＝2i(i为虚数单位)，则|z|＝(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A．1 B．‎2 C. D. ‎1．C　[解析] 因为z＝＝＝1＋i，所以|z|＝|1＋i|＝＝.‎ ‎2．L4[2014·辽宁卷] 设复数z满足(z－2i)(2－i)＝5，则z＝(　　)‎ A．2＋3i B．2－3i C．3＋2i D．3－2i ‎2．A　[解析] 由(z－2i)(2－i)＝5，得z－2i＝＝2＋i，故z＝2＋3i.‎ ‎2．L4[2014·新课标全国卷Ⅱ] ＝(　　)‎ A．1＋2i B．－1＋2i C．1－2i D．－1－2i ‎2．B　[解析] ＝＝＝－1＋2i.‎ ‎3．L4[2014·全国新课标卷Ⅰ] 设z＝＋i，则|z|＝(　　)‎ A. B. C. D．2‎ ‎3．B　[解析] z＝＋i＝＋i＝＋i，则|z|＝.‎ ‎1．L4[2014·山东卷] 已知a，b∈R，i是虚数单位，若a＋i＝2－bi，则(a＋bi)2＝(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A．3－4i B．3＋4i C．4－3i D．4＋3i ‎1．A　[解析] 因为a＋i＝2－bi，所以a＝2，b＝－1，所以(a＋bi)2＝(2－i)2＝3－4i.‎ ‎3．L4[2014·陕西卷] 已知复数z＝2－i，则z·的值为(　　)‎ A．5 B. C．3 D. ‎3．A　[解析] ∵z＝2－i，∴＝2＋i，∴z·＝(2＋i)(2－i)＝4＋1＝5.‎ ‎12． L4[2014·四川卷] 复数＝________．‎ ‎12．－2i　[解析] ＝＝－2i.‎ ‎1．L4[2014·天津卷] i是虚数单位，复数＝(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A．1－i B．－1＋i C.＋i D．－＋i ‎1．A　[解析] ＝＝＝1－i.‎ ‎11．L4[2014·浙江卷] 已知i是虚数单位，计算＝________．‎ ‎11．－－i　[解析] ＝＝＝＝－－i.‎ ‎ L5 单元综合 ‎1．[2014·济南期末] 已知复数z＝，则z的实部为(　　)‎ A．1 B．2‎ C．－2 D．－1‎ ‎1．D　[解析] 因为z＝＝＝＝－1＋2i，所以z＝－1－2i，故z的实部为－1.‎ ‎7．[2014·衡阳模拟] 若i(x＋yi)＝3＋4i(x，y∈R)，则复数x＋yi的模是(　　)‎ A．2 B．3‎ C．4 D．5‎ ‎7．D　[解析] 由i(x＋yi)＝3＋4i，得－y＋xi＝3＋4i，解得x＝4，y＝－3，所以复数x＋yi的模为＝5.‎ ‎17．[2014·湖南十三校联考] ＝________.‎ ‎17．－1　[解析] 因为＝＝i，所以＝i2014＝(－1)1007＝－1.‎ ‎　　‎ ‎2．[2014·济南期末] 执行如图X372所示的程序框图，若输入n＝7，则输出的值为(　　)‎ A．2 B．‎3 C．4 D．5‎ ‎　图X372‎ ‎2．D　[解析] 依题意可知，k＝1，n＝13；k＝2，n＝25；k＝3，n＝49；k＝4，n＝97；k＝5，n＝193>100，满足条件．故输出的值为5.‎ ‎5．[2014·衡阳模拟] 执行如图X375所示的程序框图，若输入的N的值为6，则输出的p的值为(　　)‎ A．120 B．‎720 C．1440 D．5040‎ 图X375‎ ‎5．B　[解析] 由程序框图，可得k＝1，p＝1，1<6；k＝2，p＝2，2<6；k＝3，p＝6，3<6；k＝4，p＝24，4<6；k＝5，p＝120，5<6；k＝6，p＝720，6＝6，不满足条件．故输出的p的值为720.‎ ‎10．[2014·湖南师大附中月考] 执行如图X3710所示的程序框图，则计算机输出的所有点(x，y)所满足的函数为(　　)‎ A．y＝x＋1　B．y＝2x　C．y＝2x－1　D．y＝2x 图X3710‎ ‎10．D　[解析] 由题意，该程序共输出4个点(1，2)，(2，4)，(3，8)，(4，16)，易和这4个点都在函数y＝2x的图像上．‎ ‎11．[2014·长沙模拟] 执行如图X3711所示的程序框图，若输入x＝8，则输出的k＝‎ ‎____________．‎ ‎　　　图X3711‎ ‎11．3　[解析] 依题意，得x＝88，k＝1，x<2013；x＝888，k＝2，x<2013；x＝8888，k＝3，x>2013，满足条件．故输出的k的值为3.‎